
книги / Математическое моделирование и основы научных исследований в сварке. Статистическая обработка и планирование эксперимента-1
.pdf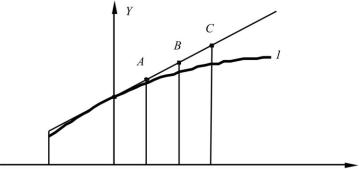
–1 |
0 |
X |
Рис. 17. Схема к расчету координат точек в направлении градиента
По результатам этих опытов определяют область оптимума. В случае k-факторов расчет крутого восхождения по оси каждого фактора производят аналогичным образом, так как коэффициенты b1 определяются независимо друг от друга. При этом движение по осям всех факторов осуществляют одно-
временно.
Шаг движения по градиенту выбирают таким, чтобы его минимальная величина была больше ошибки, с которой фиксируют фактор. Необходимо учитывать, что при движении к оптимуму малый шаг потребует значительного числа опытов, а большой шаг может привести к проскоку области оптимума. Шаг движения выбирают для одного фактора, а для остальных его рассчитывают по выражению
|
|
|
bi |
j |
, |
|
|
|
|||
|
i |
1 b |
|
||
|
|
|
1 |
1 |
|
где 1 – выбранный шаг движения для фактора l; i – шаг движения для i-го фактора; b1, bi – коэффициенты регрессии 1-го и
i-го факторов; 1, i – интервалы варьирования 1-го и i-го факторов.
81
Движение по градиенту должно начинаться от нулевой точки. Рассчитав шаг движения для каждого фактора, находят условия мысленных опытов. Мысленными называют опыты, условия проведения которых на стадии крутого восхождения установлены с учетом шага движения для каждого фактора. С целью проверки результатов крутого восхождения часть мысленных опытов реализуется.
Рассмотрим методику крутого восхождения на примере исследования модифицирования алюминия молибденом. Крутое восхождение начинаем из нулевой точки: x1 = 0,40; x2 = 840; x3 = 60; x4 – медленное охлаждение (шамотный тигель), так как быстрое охлаждение приводит к уменьшению параметра оптимизации (b4 = –9,4). Шаг движения для фактора x2 принят2 = 10 С. По приведенной выше формуле вычисляем шаг движения для факторов x1 и x3:
|
|
|
b1 |
1 |
10 |
20 0,15 |
0,0252, |
|
2 b |
|
11,9 100 |
||||||
1 |
|
|
2 |
|
|
|||
|
|
2 |
|
|
|
|
||
|
|
|
|
b3 |
3 |
|
10 |
5,1 60 |
2,57. |
|
||||||
|
|
|
|
|
|
11,9 100 |
|
|||||||||
|
3 |
|
2 b |
2 |
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Лучший результат получен в 11-м опыте (табл. 17). |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
1 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Наименование |
|
|
|
|
|
|
x1 |
|
x2 |
|
x3 |
x4 |
|
y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основной уровень |
|
|
|
|
|
|
0,40 |
|
840 |
|
60 |
– |
|
– |
||
Коэффициент bi |
|
|
|
|
|
|
|
20 |
|
1,9 |
|
–5,1 |
–9,4 |
|
– |
|
Интервал варьирования i |
|
|
|
0,15 |
|
100 |
|
60 |
– |
|
– |
|||||
bi i |
|
|
|
|
|
|
|
3 |
|
1190 |
|
–306 |
– |
|
– |
|
Шаг i |
|
|
|
|
|
0,0252 |
|
10 |
|
–2,57 |
– |
|
– |
|||
Округленный шаг |
|
|
|
|
|
|
0,03 |
|
10 |
|
–3 |
– |
|
– |
||
Мысленный опыт |
|
|
|
|
|
|
|
0,43 |
|
850 |
|
57 |
Шамотный |
|
– |
|
|
|
|
|
|
|
|
|
|
тигель |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
То же |
|
|
|
|
|
|
|
0,46 |
|
860 |
|
54 |
То же |
|
– |
|
82
О к о н ч а н и е т а б л . 1 7
Наименование |
x1 |
x2 |
x3 |
x4 |
y |
|
|
|
|
|
|
|
|
Реализованный |
0,49 |
870 |
51 |
» |
108 |
|
опыт 9 |
||||||
|
|
|
|
|
||
Мысленный опыт |
0,52 |
880 |
48 |
» |
– |
|
То же |
0,55 |
890 |
45 |
» |
– |
|
Реализованный опыт 10 |
0,58 |
900 |
42 |
» |
196 |
|
Реализованный опыт 11 |
0,61 |
910 |
39 |
» |
366 |
|
Реализованный опыт 12 |
0,64 |
920 |
36 |
» |
313 |
Величина параметра оптимизации удовлетворила исследователей, и работа была закончена. Таким образом, потребовалось 12 опытов, для того чтобы определить оптимальные условия модифицирования алюминия молибденом.
2.10.Установление вида зависимости между двумя переменными величинами
Иногда необходимо выяснить вид зависимости между двумя переменными величинами, которая может быть функциональной или стохастической. Функционально зависимыми являются такие величины, у которых каждому значению одной величины соответствует вполне определенное значение другой величины (свойства сплавов от процентного содержания того или иного элемента, величина погрешности размера изделия от температуры и др.).
Стохастически зависимыми называются такие величины, у которых различным значениям одной величины соответствуют различные законы распределения другой величины. Частным случаем стохастической зависимости является коррелятивная зависимость. Она появляется в том случае, когда каждому значению одной величины соответствуют различные средние значения другой величины (размеры изделий, обрабатываемых одновременно на одном станке, одним инструментом и т.д.).
83
Для установления вида функциональной зависимости эксперимент проводится таким образом, что для каждого значения одного признака (независимая переменная х) определяется значение другого признака (независимая переменная y), а результаты заносятся в таблицу. По этим данным строится график зависимости между величинами х и y. Полученную ломаную линию выравнивают по наиболее близкой к ней теоретической кривой.
Корреляционная зависимость. Коэффициент корреляции указывает на тесноту связи между двумя случайными величинами и изменяется от –1 до +1. При прямой линейной зависимости, т.е. когда с возрастанием значений xi увеличиваются значения yi, коэффициент корреляции kxy = +1. При обратной линейной зависимости, т.е. когда с возрастанием значений xi значения yi уменьшаются, коэффициент kxy = –1. Если х и y независимы, то kxy = 0.
При kxy 0 каждому значению xi соответствует несколько значений yi.
Для выборки небольшого объема коэффициент прямолинейной корреляции удобно определять по формуле
kxy |
|
N xi yi xi yi |
|
, |
(8) |
||
N xi2 ( xi )2 |
|
1 |
1 |
||||
|
|
2 N yi2 ( yi )2 |
2 |
|
|
||
где N – число измерений; xi и yi – значения измерений.
По величине коэффициента корреляции определяют возможность выражения функции y = f(x) в виде линейной зависимости. Значение коэффициента корреляции всегда меньше единицы. При kxy > 0,5 считают полноту связи удовлетворительной, при kxy < 0,5 регрессию следует принимать нелинейной. В случае если kxy > 0,5, уравнение регрессии можно представить в следующем виде: y = b + ax.
Значения коэффициентов a и b находят по формулам
84
a |
N xi yi |
xi yi |
; b |
yi |
a |
xi |
. (9) |
||
N xi |
xi |
2 |
N |
N |
|||||
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|||
Рассмотрим пример. Пусть имеется ряд результатов измерений значений функций y = f (x). При этом каждой величине х соответствует два значения y (табл. 18).
|
|
|
|
|
|
|
|
Т а б л и ц а |
1 8 |
||
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
y |
10 |
12 |
15 |
19 |
24 |
26 |
29 |
33 |
40 |
|
44 |
y |
12 |
14 |
17 |
21 |
27 |
28 |
32 |
36 |
43 |
|
46 |
Количество измерений N = 20. Для определения коэффициента корреляции проведем следующие расчеты:
xiyi = 1 10 + 1 12 + 2 12 + 3 15 + 4 19 + ... + 10 46 =
=3539,
xi = 2 (1 + 2 + 3 + 4 + 5 + ... + 10) = 110,
yi = 10 + 12 + 12 + 14 + 15 + 17 + ... + 44 + 46 = 529,
xi2 = 2 (12 + 22 + 32 + 42 + ... + 102) = 770,
yi2 = 102 + 122 + 122 + 142 + 152 + ... + 462 = 16 459,
( yi)2 = 5292 = 279 841, kxy = 0,994.
Полученное значение kxy показывает высокую зависимость между х и у, что дает возможность выразить линейную связь между ними в следующем виде: y = ax + b.
Определим значения коэффициентов a и b по приведенным выше формулам:
a |
20 3539 110 529 |
3,815; |
b |
529 |
3,815 |
110 |
5,468. |
|
20 770 12100 |
|
|
20 |
|
20 |
|
Таким образом, уравнение регрессии будет иметь следующий вид:
у = 3,815x + 5,468.
85
2.11. Обобщенный параметр оптимизации
Из многих параметров, характеризующих объект исследования, очень часто трудно выбрать один, самый важный. Путь к единому параметру оптимизации лежит через обобщение. Но каждый отклик имеет свой физический смысл и свою размерность. Поэтому, чтобы объединить различные отклики, необходимо ввести для каждого из них некоторую безразмерную шкалу. Шкала должна быть однотипной для всех объединяемых откликов – это делает их сравнимыми. Выбор шкалы зависит от априорных сведений об откликах, а также от той точности, с которой желательно определить обобщенный параметр.
Одним из наиболее удобных способов построения обобщенного отклика является обобщенная функция желательности Харрингтона. В основе построения этой обобщенной функции идея преобразования натуральных значений частных откликов в безразмерную шкалу желательности или предпочтительности. Для составления шкалы желательности удобно пользоваться уже разработанными таблицами соответствия.
В табл. 19 представлены числа, соответствующие некоторым точкам кривой, изображенной на рис. 18.
|
Т а б л и ц а 1 9 |
|
|
Уровень |
Отметки на шкале |
желательности |
желательности |
Очень хорошо |
1,00...0,80 |
Хорошо |
0,80...0,63 |
Удовлетворительно |
0,63...0,37 |
Плохо |
0,37...0,20 |
Очень плохо |
0,20...0,00 |
86

Рис. 18. Функция желательности
Значение частного отклика, переведенное в безразмерную шкалу желательности, обозначается через du (u = 1, 2, ..., n) и называется частной желательностью. Шкала желательности имеет интервал от нуля до единицы. Значение du = 0 соответствует абсолютно неприемлемому варианту уровня данного свойства. Понятию «очень хорошо» соответствуют значения на шкале желательности 1 > du > 0,8, а понятию «очень плохо» 0 < du < 0,2 и т.д. Выбор отметок на шкале желательности 0,63 и 0,37 не случаен, это объясняется удобством вычислений: 0,63 (1 – 1 е), 0,37 1 е. Значение du = 0,37 обычно соответствует границе допустимых значений.
Точки кривой (см. рис. 18) задаются уравнением d = exp[–exp(–y ' )].
87

На оси ординат нанесены значения желательности, изменяющиеся от 0 до 1. По оси абсцисс указаны значения отклика, записанные в условном масштабе. За начало отсчета 0 по этой оси выбрано значение, соответствующее желательности 0,37. Выбор именно этой точки связан с тем, что она является точкой перегиба кривой, что в свою очередь создает определенные удобства при вычислениях. То же самое верно для значения желательности, соответствующего 0,63. Кроме того, эта кривая хорошо передает тот факт, что в областях желательности, близких к 0 и 1, «чувствительность» ее существенно ниже, чем в средней зоне.
Симметрично относительно нуля на оси y ' (y ' – кодированная шкала) расположены кодированные значения отклика. Значение на кодированной шкале принято выбирать от 3 до 6. Например, на рис. 18 использовано шесть интервалов в сторону убывания и шесть – в сторону возрастания. Выбор числа интервалов определяет крутизну кривой в средней зоне.
После того как выбрана шкала желательности и частные отклики преобразованы в частные функции желательности, приступают к построению обобщенного показателя D, названного Харрингтоном обобщенной функцией желательности. Обобщать, т.е. переходить от di к D, предлагается по формуле
n |
|
D n du . |
(10) |
u 1 |
|
Здесь обобщенная функция желательности задается как среднее геометрическое частных желательностей. Примером может служить установление пригодности материала с данным набором свойств для использования его в определенных условиях.
Если хотя бы один частный отклик, входящий в комплекс параметров качества материала, не удовлетворяет требованиям технических условий (например, при определенной температуре
88
материал становится хрупким и разрушается), то как бы ни были хороши прочие свойства, материал не может быть использован по назначению. Действительно, способ задания обобщенной функции желательности таков, что если хотя бы одна частная желательность равна нулю, то обобщенная функция тоже будет равна нулю. С другой стороны, D = 1 тогда и только тогда, когда все du = 1 (u = 1, 2, ..., n). Обобщенная функция желательности весьма чувствительна к малым значениям частных желательностей.
Способ задания базовых отметок шкалы желательности, представленный в табл. 19, один и тот же как для частных желательностей, так и для обобщенной. Так, если d1, d2, ...,
dn = 0,63, то и D = 0,63, если d1, d2, ..., dn = 0,37, то и D = 0,37 и
т.д. В обобщенную функцию желательности могут входить самые разнообразные частные отклики: технологические, технико-экономические, экономические, эстетические и т.д. Построение обобщенного параметра оптимизации связано с созданием единого признака, количественно определяющего функционирование исследуемого объекта со многими выходными параметрами. Каждый выходной параметр (отклик) имеет свой физический смысл, свою размерность. Чтобы объединить различные отклики, необходимо ввести единую для всех откликов безразмерную шкалу в соответствии с некоторым стандартным аналогом. Шкала должна быть однотипной для всех объединяемых откликов. Построение шкалы во многом зависит от уровня априорных сведений о выходных параметрах, а также от той точности, с которой мы хотим определить обобщенный отклик.
2.12. Принятие решений в экстремальном эксперименте
Невозможность полной формализации исследований вызывает необходимость активного вмешательства экспериментатора в процесс исследования. Неформальная задача экспериментатора состоит в том, что он по некоторым
89
характерным признакам выбирает решение из множества неформализованных решений, определяющих стратегию экстремального эксперимента.
Планирование экстремального эксперимента сопряжено с необходимостью принятия решений до начала и после завершения каждой серии итерационного цикла исследования на основании анализа априорных данных и результатов проведенного эксперимента. Для этого необходимо располагать сведениями об адекватности модели, значимости коэффициентов регрессии, иметь информацию о расположении области оптимума и т.д. В подразд. 2.8 рассмотрены некоторые рекомендации по принятию решений. В данном подразделе они расширены.
Если модель адекватна и все ее коэффициенты значимы, то предполагается (при отсутствии других точных сведений), что область оптимума далека. В такой ситуации приемлемо движение по градиенту линейного полинома для достижения оптимума по всем факторам.
При получении неадекватной линейной модели можно достроить план для повышения степени полинома или с целью получения уравнения регрессии, коэффициенты которого не смешаны либо смешаны с незначительными эффектами. Подходящим решением в этой ситуации также является движение к оптимуму.
Более сложные ситуации возникают, когда все коэффициенты или их часть оказываются статистически незначимыми. В таких ситуациях экспериментатор, используя априорную информацию, последовательно выдвигает и анализирует ряд конкурирующих гипотез о близости незначимых факторов к оптимуму, о величине интервала варьирования, об ошибке эксперимента и о смешении линейных коэффициентов со значимыми эффектами взаимодействия. Рассмотрим случаи, когда выдвигаемые эффекты не отвергаются.
90
