книги / Математическое моделирование и основы научных исследований в сварке. Статистическая обработка и планирование эксперимента-1

1.Незначимые эффекты близки к оптимальным значениям.

Вслучае если незначимы все коэффициенты регрессии, то необходимо достроить план для описания поверхности отклика полиномом второго порядка. Если незначима часть коэффициентов и линейная модель адекватна, необходимо осуществить крутое восхождение по значимым факторам, застабилизировав при этом незначимые. При незначимости части коэффициентов и неадекватности линейной модели можно достроить план до неполного квадратного уравнения, использовав план меньшей дробности.

2.Мал интервал варьирования. Такая гипотеза не отвергается, если ошибка эксперимента невелика и предполагается, что оптимум по незначимым факторам не достигнут.

Вэтой ситуации при незначимости всех коэффициентов следует построить новый план, увеличив при этом интервалы варьирования и перенеся центр плана в точку с лучшим опытом в анализируемой серии. При незначимости части коэффициентов и адекватности линейной модели необходимо совершить крутое восхождение по значимым факторам.

3.Велик интервал варьирования. В этом случае при незначимости всех коэффициентов и неадекватности линейной модели можно уменьшить либо интервал варьирования, либо дробность реплики, а при незначимости части коэффициентов и адекватности модели совершить крутое восхождение по значимым факторам.

4.Велика ошибка эксперимента. Такая гипотеза при-

нимается в том случае, если отвергается предположение о малом интервале варьирования. При незначимости всех коэффициентов в этой ситуации необходимо увеличить число параллельных опытов или построить план меньшей дробности. В случае незначимости части коэффициентов и адекватности модели нужно совершить крутое восхождение по значимым факторам или уменьшить дробность реплики.

91

5. Главные эффекты смешаны со значимыми эффектами взаимодействия. В этой ситуации при незначимости части коэффициентов необходимо совершить крутое восхождение по градиенту адекватной линейной модели. При незначимости всех коэффициентов можно построить план, уменьшив дробность реплики.

Если проведенные опыты показали, что крутое восхождение эффективно и совершалось в том случае, когда все коэффициенты регрессии были значимы, то необходимо провести серию опытов в новых условиях. Центром плана новой серии опытов следует выбрать координаты лучшей или близкой к ней точки крутого восхождения. Если же крутое восхождение совершалось в случаях, когда часть эффектов была незначима, то в следующем итерационном цикле следует устранить причины незначимости, застабилизировав факторы, достигшие оптимальных значений (или не влияющих на процесс), изменив интервалы варьирования, увеличив число параллельных опытов или изменив систему смешения эффектов.

Если гипотеза о близости области оптимума не отвергается, а крутое восхождение неэффективно, то можно окончить исследования или достроить план для описания процесса полиномом второго порядка.

2.13.Функции для проведения регрессии

впакете Mathcad

Ранее было показано, как расчетным путем определить коэффициенты a и b в уравнении y = ax + b, если есть область исходных точек x и y. Для проведения линейной регрессии в пакете Mathcad имеется ряд встроенных функций для двухпараметрической зависимости y(x):

intercept(X,Y) – возвращает значение коэффициента b (смещение линии регрессии по вертикали);

92

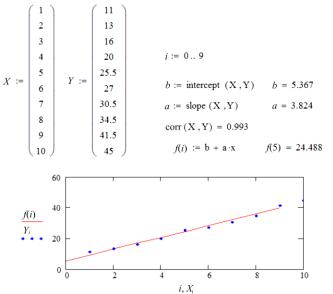
slope(X,Y) – возвращает значение коэффициента a (характеризует наклон линии регрессии).

На рис. 19 приведен пример построения линейной функции.

Рис. 19. Листинг проведения линейной регрессии и график функции регрессии и исходных точек

93

3.МАТРИЧНЫЙ ПОДХОД

КРЕГРЕССИОННОМУ АНАЛИЗУ

3.1.Метод наименьших квадратов для одного фактора

Статистика разработала множество разнообразных методов обработки экспериментальных данных. Самым распространенным из них является метод наименьших квадратов, который был разработан Лежандром и Гауссом еще более 170 лет назад.

Рассмотрим этот метод на простом примере: один фактор, модель линейная. Функция отклика имеет вид

y b0 b1 x1.

Это всем хорошо известное уравнение прямой линии. Наша цель – вычисление неизвестных коэффициентов b0 и b1. Если бы при проведении опытов все экспериментальные точки лежали строго на прямой линии, то для каждой из них справедливым являлось бы равенство

y b0 b1 x1i 0 ,

где i = 1, 2, ..., N – номер опыта. В этом случае не было бы никаких проблем. На практике указанное равенство нарушается и вместо него используют следующее уравнение:

y b0 b1 x1i ξi ,

где i – разность между экспериментальным и вычисленным по уравнению регрессии значениями y в i-й экспериментальной точке. Эту величину иногда называют невязкой.

Действительно, невязки возникают по двум причинам: изза ошибки эксперимента и из-за непригодности модели. Как правило, эти причины смешаны, и трудно, не получив дополнительной информации, судить, какая из них преобладает.

94

Можно постулировать, что модель пригодна. Тогда невязка будет порождаться только ошибкой опыта. (Можно, конечно, постулировать, что ошибка опыта равна нулю. Тогда невязка будет связана только с пригодностью модели и пригодной будет такая модель, для которой все невязки равны нулю.)

Необходимо найти такие коэффициенты, при которых невязки будут минимальными. Одним из самых распространенных методов является метод наименьших квадратов (МНК), который записывается следующим образом:

i 1

МНК обладает замечательным свойством – он делает число уравнений равным числу неизвестных коэффициентов.

Наше уравнение регрессии имеет вид

yb0 b1 x1 .

Внем два неизвестных коэффициента. Значит, применяя МНК, мы получим два уравнения. Рассмотрим, как они получаются. Уравнение (11) можно переписать иначе:

Известно, что минимум некоторой функции, если он существует, достигается при одновременном равенстве нулю частных производных по всем неизвестным, т.е.

Отсюда получим следующие уравнения:

N

2 yi b0 b1 x1i 0;

i 1

95

N

2 ( yi b0 b1 x1i ) x1i 0.

i 1

После преобразований и решения уравнений получим окончательные формулы для вычисления коэффициентов:

Предварительно рассмотрим численный пример линейного уравнения для одного фактора в общем виде. Затем этот же пример опишем на матричном языке.

Пусть известно, что y связан с х1 линейным уравнением

yb0 b1 x1 .

Врезультате проведенного эксперимента были получены

результаты, представленные в табл. 20. Здесь х1 принимает пять кодированных значений.

Та б л и ц а 2 0

96

По приведенным ранее формулам вычислим коэффициенты:

Следовательно, полученное уравнение имеет вид

y 2 1 x1 .

Для решения этой же задачи воспользуемся матричным методом. В приведенном примере участвуют три множества: элементы, задающие условия проведения опытов; элементы, характеризующие их результаты; неизвестные коэффициенты, которые нужно определить. Так, элементам, характеризующим результаты опытов, соответствует столбец Y; неизвестным коэффициентам – столбец В; элементам, задающим условия опытов, – столбец Х.

В таблице для Х появился столбец х0, состоящий из +1. Он введен для удобства вычислений всех коэффициентов, включая b0. Фактически это означает, что мы переписали исходное

97

уравнение следующим образом: y b0 x0 b1 x1 . Таблицы, в

которых собраны упорядоченные некоторым образом элементы, называются матрицами. Следовательно, в нашем случае Y, B и X являются матрицами. Элементы Y упорядочены по номерам опытов, элементы Х, кроме того, – по номерам переменных (х0, х1), а элементы В – по номерам коэффициентов, которые соответствуют номерам переменных.

3.2. Некоторые операции над матрицами

Матрицы, описанные в предыдущем подразделе, различаются по числу элементов, числу строк и числу столбцов. Если число строк и столбцов различно, то матрицы называются прямоугольными, а при равном числе строк и столбцов – квадратными. Все матрицы из этого примера – прямоугольные. Если матрица имеет один столбец, то ее называют матрицейстолбцом или вектором-столбцом. Примерами служат матрицы Y и B. Аналогично можно определить и матрицы-строки (век- торы-строки).

На основании исходных данных рассматриваемого примера можно записать систему из пяти уравнений по одному уравнению для каждого опыта:

0 = b0 1 + b1 (–2); 1 = b0 1 + b1 (–1); 2 = b0 1 + b1 (0); 3 = b0 1 + b1 (+1); 4 = b0 1 + b1 (+2).

На матричном языке эта система уравнений выглядит следующим образом:

98

Чтобы эти две записи стали эквивалентными, необходимо ввести определенные правила перемножения матриц. В произведении необходимо различать матрицу, стоящую слева, и матрицу, стоящую справа. Перемножить две матрицы – значит получить матрицу произведений, элементы которой находятся по следующим правилам.

Элементы первой строки матрицы, стоящей слева, умножаются на соответствующие элементы матрицы, стоящей справа, и полученные произведения складываются. В нашем случае имеем

(+1) b0 + (–2) b1.

Для получения элемента, стоящего на пересечении первого столбца и второй строки, аналогичная операция проделывается со второй строкой матрицы, стоящей слева, и с тем же самым первым столбцом матрицы, стоящей справа, т.е.

(+1) b0 + (–1) b1.

Продолжая таким образом до последней строки матрицы, стоящей слева, получаем все элементы первого столбца матрицы произведений. Эта процедура повторяется столько раз, сколько векторов-столбцов содержит матрица, стоящая справа. В нашем случае эта матрица имеет только один столбец. Из определения видно, что матрица произведений имеет столько столбцов, сколько матрица, стоящая справа, и столько строк, сколько матрица, стоящая слева. В рассматриваемом примере матрица-произведение имеет один столбец и пять строк, что

99

соответствует размерности матрицы Y. Матрица-произведение имеет вид

1 b0 b1 ( 2)1 b0 b1 ( 1)1 b0 b1 (0) .1 b0 b1 ( 1)1 b0 b1 ( 2)

Сопоставление матрицы-произведения с системой уравнений показывает тождественность матричной и нематричной форм записей. Вектор Y, оказывается, и есть матрица произведений в данном случае. В правилах перемножения матриц существуют особенности – левая и правая матрицы неравномерны. Для двух произвольных матриц произведение существует, если число столбцов матрицы, стоящей слева, равно числу строк матрицы, стоящей справа. Отсюда ясно, что для двух квадратных матриц одинакового размера существуют оба произведения (справа и слева), однако они могут быть различными. Матрицы, произведение которых не зависит от порядка сомножителей, называются коммутирующими. В общем же случае для произведения матриц коммутативный закон не выполняется.

Система нормальных уравнений МНК в нашем случае выглядит следующим образом:

5 b0 + 0 b1 = 10; 0 b0 + 10 b1 = 10.

В матричном виде система нормальных уравнений будет иметь вид

X T X B X T Y .

Здесь X T обозначает матрицу, транспонированную по отношению к матрице Х. Протранспонировать матрицу – это значит столбцы исходной матрицы сделать строками транс-

100