книги / Теория механизмов и механика систем машин

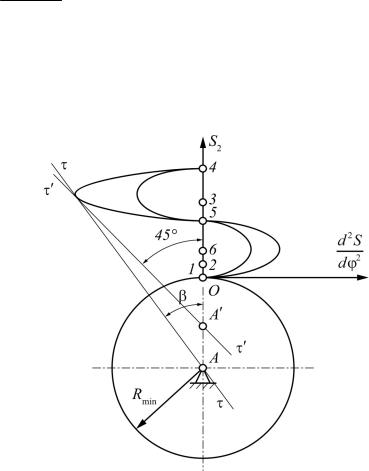
d 2S

или d 2 tg45 . (6.2)

Rmin S

Последнее условие позволяет провести следующее графическое построение (рис. 6.21). По диаграммам S f ( ) и d 2S / d 2 f ( ) строим совмещенный график S f (d 2S / d 2 ).

Для этого производим разметку перемещений звена 2 по оси OS2 и откладываем на проведенных горизонтальных пря-

мых значения d 2S / d 2 . Соединив полученные точки плавной кривой, получаем диаграмму

Sf (d 2S / d 2 ).

Втой части диаграммы, которая соответствует отрицательным максимальным значениям

d 2S / d 2 , проводим под углом 45° к оси S2 касательную τ'–τ' к кривой диаграммы и получаем точку A' и минимальный радиус кулачка при данном угле 45°.

Согласно неравенству (6.2) центр вращения А кулачка должен быть расположен ниже точки A'. Величина отрезка АО в масштабе построения дает величину Rmin.

6.9. Проектирование кулачкового механизма аналитическим методом

6.9.1. Алгоритм проектирования кулачкового механизма

При проектировании кулачкового механизма рекомендуется следующий порядок действий:

1. После ознакомления с исходными данными и условиями работы механизма составить блок-схему для программы на языке РASКAL, BASIК и др. по расчету и проектированию кулачкового механизма. Ознакомившись с инструкцией по вводу данных в программу SK11, исходные данные офор-

141

мить на бланке ФОРТРАН или ввести их с дисплея. Алгоритм расчета при проектировании кулачкового механизма представлен на рис. 6.22.

значений

Рис. 6.22. Алгоритм расчета кулачкового механизма

142

2.Для овладения практическими навыками численного и графического интегрирования вычертить на листе графики ускорения, скорости и перемещения, т.е. выполнить кинематический анализ. Сопоставить с результатами вычислений на компьютере и рассчитать масштабы изображенных величин.

3.На фазовой плоскости ( B , 1, SB ) изобразить фазовый портрет для

конкретной схемы механизма, определить область допустимых решений (ОДР) для заданных условий работы кулачкового механизма и выбрать в этой области положение оси O1 вращения кулачка. Сопоставить выбранные

размеры с результатами расчетов на компьютере.

4.Построить профиль кулачка по результатам вычислений на компьютере и показать методику определения координат двух–трех точек графическими построениями.

5.Построить график изменения угла давления в функции угла поворота кулачка. На профиле кулачка показать максимальные углы давления 3 и

F13 и 14 F14 и сравнить их с допускаемым углом давления доп .

6. Оформить пояснительную записку по разделу «Проектирование кулачкового механизма», показав в ней алгоритм расчетов, методику ввода и вывода данных, и приложить распечатку результатов расчета.

6.9.2. Кинематический анализ кулачкового механизма

143

кулачка;

e, Rmin – соответственно эксцентриситет и минимальный радиус кулачка;

В дальнейшем будем считать заданными:

1)уравнение центрового профиля кулачка;

2)расстояние а;

3)эксцентриситет е;

4)угловую скорость ω;

5)текущий фазовый угол.

Требуется определить координаты xT , yT точки встречи толкателя с

точкой профиля кулачка при повороте последнего на угол φ, а также скорость в данный момент.

Определим минимальный радиус. Из рис. 6.23 следует:

Определим на профиле кулачка координаты точки М, которая окажется в контакте с толкателем при повороте кулачка на заданный фазовый угол φ. Для этого необходимо совместно решить уравнение профиля кулачка и уравнение прямой у = kx +b, изображающей положение толкателя в обращенном движении (см. рис. 6.23).

Составим уравнения упомянутой прямой в системе хОу. Угловой коэффициент этой прямой равен tg (90 – φ). Отрезок, отсекаемый на оси Оу (с учетом знака) и равный ОK2, определяется из следующих условий (см.

рис. 6.23):

nO1 cose ,

144

отсюда

Тогда уравнение искомой прямой с учетом углового коэффициента и выражения (6.8) примет следующий вид:

145

Определим xT , yT – ординаты точки M0 встречи толкателя с точкой М на профиле кулачка. В соответствии с рис. 6.23 имеем

Дифференцируя (6.16) по времени, получим абсолютную скорость толкателя при повороте кулачка на заданный угол:

Производные dxdtM и dydtM определяются по формулам (6.12). Диффе-

ренцируя по времени выражение (6.17), можно определить ускорение толкателя.

146

7. ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

7.1. Назначение зубчатых передач и требования к ним

Зубчатые механизмы служат для передачи непрерывного вращательного движения и крутящих моментов, а также для изменения скорости вращения. Зубчатые передачи осуществляют передачу вращательного движения между валами с любым заданным отношением угловых скоростей: как с постоянным, так и с переменным.

В современном машиностроении наибольшее распространение получили зубчатые колеса, профили которых очерчены по эвольвенте круга. Такие зубчатые колеса называются эвольвентными.

Широкое распространение эвольвентных зубчатых колес объясняется их преимуществами перед колесами иных профилей.

Методом обкатки, пользуясь стандартным инструментом, можно получить колеса, нарезанные со смещением режущего инструмента и без смещения. Это является одним из важных преимуществ изготовления эвольвентных зубчатых колес.

Колеса, изготовленные без смещения режущего инструмента, могут работать с любым эвольвентным колесом, также изготовленным без смещения инструмента, того же модуля независимо от его числа зубьев. Поэтому эвольвентные колеса широко применяются в сменных передачах.

Зубчатая передача должна обеспечивать плавную и безударную работу с минимальным износом зубьев колес. Для этого необходимо, чтобы зубья колес были неподрезанными и незаостренными, передача – свободной от заклинивания; коэффициент перекрытия 1,0 ; передача обеспечивала опреде-

ленное удельное скольжение ν, оценивающее интенсивность износа зубьев. Коэффициенты и ν называются качественными показателями пере-

дачи. Они определяются геометрическими параметрами передачи, которые, в свою очередь, зависят от коэффициентов смещений X1 и X2. Следовательно, варьируя коэффициенты смещений, можно влиять на качественные показатели передачи (табл. 7.2–7.5).

7.2. Основная теорема зацепления зубчатых колес

На рис. 7.1 показаны части двух зубчатых колес (1, 2), вращающихся с угловыми скоростями ω1 и ω2. O1O2 – линия межосевого расстояния; N1N2 – общая нормаль к соприкасающимся профилям зубьев в точке C; P – точка пересечения нормали N1N2 с линией O1O2. Отрезки прямых O1N1, O2N2 пер-

147

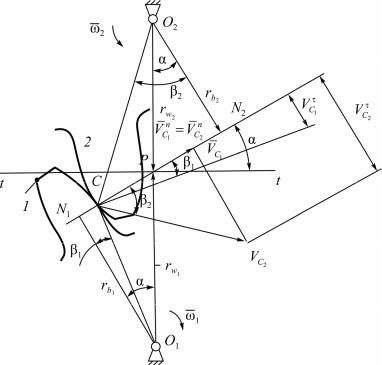
пендикулярны к линии N1N2 и обозначены rb1, rb2. Отрезки прямой O1P, O2P обозначены rw1, rw2, α – угол наклона нормали N1N2 к прямой tt, которая перпендикулярна к линии O1O2; VC1 – скорость точки С профиля зуба первого колеса; VC2 – скорость точки С профиля зуба второго колеса.

Рис. 7.1. План зацепления

Спроектируем VC1 и VC2 на направление нормали N1N2, получим нормальные составляющие этих скоростей VCn1 и VCn2 , которые должны быть

равны между собой по величине и иметь одинаковое направление, так как в противном случае зубья будут либо врезаться один в другой, либо отходить один от другого, что не имеет места при твердом материале зубьев и постоянном их контакте за время зацепления.

Следовательно,

Используя рис. 7.1, уравнение (7.1) можно преобразовать следующим образом:

VCn1 cos VCn2 cos 2 ;

1СО1 cos 1 2СО2 cos 2 ;

1rb1 2rb2 ,

где rb1 и rb2 – радиусы основной окружности колес;

148

1rw1 cos 2rw2 cos ,

где rw1 и rw2 – радиусы начальной окружности колес. Окончательно получим

На основании равенства (7.1) можно сделать вывод: общая нормаль к сопряженным профилям зубьев делит линию межосевого расстояния на части, отношение которых обратно пропорционально отношению угловых скоростей колес.

В этом и заключается основная теорема зубчатого зацепления. Для зубчатой передачи i1−2 = const равенство (7.2) примет вид

Уравнение (7.3) позволяет сделать следующее заключение. Для того чтобы передаточное отношение было постоянным, профили зубьев должны быть очерчены по кривым, удовлетворяющим следующему правилу: общая нормаль в процессе соприкосновения их должна проходить через одну и ту же точку, лежащую на линии межосевого расстояния, и делить ее в постоянном отношении, т.е.

rw2 const. rw1

7.3. Эвольвентный профиль зуба

149

в) отрезок AN касательной равен радиусу кривизны эвольвенты в точке А;

г) длина дуги A0N равна радиусу кривизны, т.е. отрезку АN.

Любая точка А на эвольвенте характеризуется ее полярными координатами: радиусом r = ОА и углом θ.

Уравнения эвольвенты представляют собой зависимости параметров r и

Величину = tg α – α называют эвольвентным углом профиля зуба (или инволютой α) и обозначают inv α.

Из треугольника OAN (см. рис. 7.2)

Уравнения (7.4) и (7.5) являются уравнениями эвольвенты, их определяют через параметры α и rb, полярные координаты r и любой ее точки.

7.4. Основные размеры нормальных зубчатых колес

Все зубья одного колеса имеют одинаковые размеры. Окружность, ограничивающая зубья в их выступающей части, называется окружностью вершин зубьев зубчатого колеса.

Окружность, ограничивающая глубину впадины между зубьями, называется окружностью впадин зубчатого колеса.

Окружность, для которой модуль есть величина стандартная, называется делительной окружностью.

Расстояние между делительной окружностью и окружностью вершин зубьев зубчатого колеса, измеряемое по радиусу, называется высотой головки зуба. Расстояние между делительной окружностью и окружностью впадин, измеряемое по радиусу, – высота ножки зуба. Следовательно, делительная окружность делит зуб на головку и ножку.

Обозначим через ra радиус окружности вершин; rf – радиус окружности впадин; ha – высоту головки зуба; hf – высоту ножки зуба. Получим следующие соотношения:

150