
книги / Нечёткое, нейронное и гибридное управление
..pdf
нормализации терм-множества в диапазоне (–1…+1) разбиваем его, например, на пять интервалов (рис. 2.34):
Y1 1; 0,6 ;
Y1 0,6; 0,2 ;
Y1 0,2; 0,2 ;
Y1 0,2; 0,6 ;
Y1 0,6; 1 .
Далее применяем метод наименьших квадратов к функционалу
F (W1 X1 W2 X2 W3 X3 W4 X4 W5 X5 Yi )2 .
Рис. 2.34. К разбиению на подинтервалы нормированного интервала
Взяв производную от функции F по каждому синапсу на каждом из 5 интервалов и приравняв их к нулю, получим
F |
2(W X |
W X |
|
W |
0 |
W |
0 |
W |
0 |
Y ) 0; |
|
|
2 |
||||||||||
1 |
1 |
2 |
3 |
|
4 |
|
5 |
|
i |
||
W1 |
|
|
|
|
|
|
|
|
|
|
|
201

F |
2(W X |
W X |
|
W |
X |
|
W |
0 W |
0 Y ) 0; |
|
|
2 |
3 |
||||||||
1 |
1 |
2 |
3 |
|
4 |
5 |
i |
|||
W2 |
|
|
|
|
|
|
|
|
|
|
F |
2(W 0 |
W X |
|
W X |
|
W |
X |
|
W |
0 |
Y ) 0; |
||||||
|
|
2 |
3 |
4 |
|||||||||||||
1 |
|
2 |
3 |
|
4 |
|
|
5 |
|
|
i |
||||||
W3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F |
2(W |
0 W 0 W X |
|
W X |
|
|
W X |
|
Y ) 0; |
|||||||
|
|
3 |
4 |
5 |
|||||||||||||
1 |
|
2 |
|
3 |
|
|
4 |
5 |
|
i |
|||||||
|
W4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
2(W |
0 W 0 W 0 W X |
|
W X |
|
Y ) 0. |
|||||
|
|
4 |
5 |
|||||||||
1 |
2 |
3 |
|
4 |
5 |
i |
||||||
|
W5 |
|
|
|
|
|
|
|
|
|
|
|
После преобразований получим |
|
|
|
|
|
|
||||||
|
|
|
|
F |
W X |
W X |
|
Y 0; |
|
|
||
|
|
|
|
|
2 |
|
|
|||||
|
|
|
1 1 |
2 |
i |
|
|
|
|
|||
|
|
|
|
W1 |
|
|
|
|
|
|
|
|
|
F |
W X |
W X |
|
W |
X |
|
Y |
0; |
||
|
|
|
2 |
3 |
|||||||
1 |
1 |
2 |
3 |
|
i |
|
|||||
|
W2 |
|
|
|
|
|
|
|
|
||
|
F |
W X |
|
W X |
|
W |
X |
|
Y |
0; |
|
|
|
2 |
3 |
4 |
|||||||
2 |
3 |
4 |
i |
||||||||
W3 |
|
|
|
|
|
|
|
|
|||
F |
W X |
|
W X |
|
W X |
|
Y |
0; |
||||||
|
|
3 |
4 |
5 |
||||||||||
3 |
|
|
4 |
|
|
5 |
i |
|
||||||
W4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
F |
W X |
|
W X |
|
Y |
0. |
|
|||||
|
|
|
4 |
5 |
|
|||||||||
|
W5 |
|
4 |
|
|
5 |
|
i |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выразим синапсы (весовые коэффициенты) следующим обра-
зом:
W1 Yi W2 X2 ; X1
202

W2 Yi W1 X1 W3 X3 ;
X2
W |
Yi W2 X2 |
W4 X4 |
; |
(2.6) |
|||||
|
|
|
|
||||||
3 |
|
|
|
X3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
Yi W3 X3 W5 X5 |
; |
|
|
|||||
|
|
|
|
|
|||||
4 |
|
|
|
X4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
Yi W4 X4 |
. |
|
|
|
|||
|
|
|
|
||||||
5 |
|
X5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
В формулах (2.6) Yi – есть текущее значение переменной вели-
чины, подаваемое на вход фаззификатора и в то же время есть задания следящей системы, которые должны изменяться синхронно.
При первом отсчете начальные значения синапсов задаются случайным образом, а в дальнейшем за исходные принимаются значения синапсов предыдущего отсчета. При этом каждый раз значения синапсов (в зависимости от того, какому интервалу принадлежит желаемый Y) автоматически подстраиваются под новые значения. В случае если отклонение вышло за нормированный диапазон,
то W1 Y1 и W5 Y1.
Модифицированный алгоритм наименьших квадратов применим только для линейных терм, поддиапазоны которых равны и равномерно расположены в нормированном интервале.
Число терм терм-множества фаззификатора всегда должно быть равно числу подинтервалов разбиения нормированного интервала. В случае включения регулятора терм модификация метода наименьших квадратов недопустима. В дальнейшем предлагается метод адаптации с минимальными итерациями или метод с последовательным обучением (рассмотренный выше).
203
Алгоритм последовательного обучения нейрона с обратной связью
Рассмотрим метод адаптации с последовательным обучением [44]. Данный метод относится к методам последовательной идентификации линейных систем в реальном времени, который основан на принципе обучения с моделью и в котором получена модель импульсной характеристики. Аналогично методам стохастической аппроксимации метод последовательного обучения не дает оценки параметров по методу наименьших квадратов на различных последовательных шагах, вследствие чего сходимость этого метода несколько ниже, чем метод последовательной регрессии. При этом оценки постепенно сходятся (в среднем) к истинным значениям параметров. Метод последовательного обучения отличается от метода стохастической аппроксимации характеристиками сходимости. Этот метод удобно применять для процессов с медленно изменяющимися параметрами. Основное преимущество метода последовательного обучения состоит в простоте алгоритма адаптации.
В методе последовательного обучения рассматривается линейная система со случайным входом u(t), выходом x(t) и импульс-
ной характеристикой g(t). Связь между входом и выходом описы-
вается интегралом свертки, который для нулевых начальных условий записывается в виде
|
x(t) t |
g( )u(t )d |
|
|
(2.7) |
|
|
0 |
|
|
|
|
|
где u(t ) |
– измеряемая величина. |
|
|
|
|
|
Дискретная форма интеграла свертки |
|
|
|
|||
|
|
N |
|
|
|
|
|
xj giu j i . |
|
|
(2.8) |
||
|
|
i 1 |
|
|
|
|
Определение импульсной реакции |
gi выполняется путем ите- |
|||||
рационных |
вычислений множества |
величин: |
( j) , ( j) ,..., ( j) , |
|||
|
|
|
|
1 |
2 |
N |
204 |
|
|
|
|
|
|
j N 1, N 2,..., которые должны, соответственно, приближаться к g1,..., gN в уравнении (2.8), где j обозначает номер итерации.
Тогда оценка выхода модели (нейрона) x |
jм |
при использовании ( j) |
|
|
|
i |
|
равна по аналогии с (2.9): |
|
|
|
N |
|
|
|
xjм i( j)u j i . |
(2.9) |
||
i 1
Обозначая
gg1,..., gN Т ,
j 1 ( j),..., N ( j) T ,
|
|
|
|
ui |
|
|
|
|
T |
, |
|
|
|
||
|
|
|
|
u j 1 |
,..., u j N |
|
|
|
|||||||
преобразуем (2.8) и (2.9) соответственно к виду |
|
|
|
||||||||||||
|
|
|
|
|
|
|
xj gT u j , |
|
|
|
|
|
|||
|
|
|
|
|
|
xjм Tj u j . |
|
|
|
|
|
||||
Определяем разность |
|
|
|
|
|
|
|
|
|
|
|
||||
x |
j |
x |
jм |
(g |
j |
)T u |
j |
uT (g ) uT |
|
. |
|||||
|
|
|
|
|
|
j |
|
i |
j |
j |
|
||||
Рассмотрим вектор |
j 1 |
j , |
который будем использо- |
||||||||||||
вать для коррекции вектора следующей идентификацией j 1 отно-
сительно j |
с учетом ошибки (xj |
xjм ) |
в оценке xj . |
||||||||
Полагая |
|
|
(x |
|
x |
|
) |
u j |
, где |
j 1,2,... , получим рекур- |
|
j |
j |
jм |
uTj u j |
||||||||
|
|
|
|
|
|
|
|||||
рентную формулу
205
|
|
|
|
(x |
|
x |
|
) |
u j |
. |
(2.10) |
j 1 |
j |
j |
jм |
|
|||||||
|
|
|
|
|
uTj u j |
|
|||||
Чтобы начать процедуру оценивания ошибки согласно (2.10), при j = 1 можно подставить xjм 0.
Если в (2.10) ввести коэффициент коррекции ошибки С, то получим окончательное выражение рекуррентной формулы:
|
|
|
|
C(x |
|
x |
|
) |
u j |
, при 0 С 2. |
(2.11) |
j 1 |
j |
j |
jм |
|
|||||||
|
|
|
|
|
uTj u j |
|
|||||
Пример 2.3. Рассмотреть применение рекуррентной формулы (2.11) для адаптации нейрона.
Пусть терм-множество фаззификатора имеет вид, где при текущем отклонении u j 0,4 активизировались термы Н и ПС с
формированием степеней принадлежности ПБ 0,4 и ПС 0,6. Запишем (2.11) в новых обозначениях при условии С = 1:
|
|
|
|
|
|
|
|
|
|
|
|
C j |
|
ПБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
j 1 j |
|
|
|
ПС |
|
, |
|
|
|
|||||||||
|
|
|
2 |
2 |
2 |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ОБ |
ОС |
|
|
ПС |
ПБ |
|
|
|
|
|
где u j ( ПБ ПБ ПС ПС ). |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Расчет первой итерации |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
u j (0)ПБ ПБ |
|
|
|
|
|
|
|
|
|||||
|
(1) |
|
(0) |
|
|
(0)ПС ПС |
ПБ |
|
|
||||||||||||
ПБ |
|
ПБ |
|
|
|
|
|
|
|
|
|
|
|
ПС |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПБ |
2 |
ПС 2 |
|
|
|
||||||||||
(1)ПС |
|
(0)ПС |
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
(0,4) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
0,3077 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
0,4 |
2 |
|
0,6 |
2 |
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
|
0,4615 |
|
|
|
|
|
|
|
|
|
||||||
Расчет второй итерации:
206
|
|
|
|
|
|
u j |
(1)ПБ ПБ (1)ПС |
|
|
|
|
|
||||
|
(2) |
|
|
(1) |
|
ПС |
|
ПБ |
|
|
||||||
ПБ |
ПБ |
|
|
|
|
|
|
ПС |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПБ |
2 ПС |
2 |
|
|
|
||||||||
(2)ПС |
|
(1)ПС |
|
|
|
|
|
|
||||||||
|
|
|
|
|
(0,4 0,3077 0,4 |
0,4615 |
0,6) |
0,4 |
|
|||||||
|
0,3077 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
2 |
0,6 |
2 |
|
|
|
|
|
|||||
|
0,4615 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
0,3077 |
|
0 |
0,3077 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
0,4615 |
|
0 |
0,4615 |
|
|
|
|
|
|
|
|
|
|||
Таким образом, потребовалась одна итерация на данном шаге, вторая итерация приведена только для доказательства, подтверждающего повторяемость результата.
Из анализа рассмотренных алгоритмов предпочтение следует отдать методу с последовательным обучением за его быстродействие и возможность использования как линейных, так и нелинейных терм.
2.9.Примеры применения адаптивных нейронов
собратной связью
2.9.1. Адаптивный нечеткий регулятор напряжения синхронного генератора
Рассмотрим адаптивный нечеткий регулятор напряжения бесщеточного синхронного генератора (БЩСГ) с применением нейронной технологии [17].
На рис. 2.35 приведена структурная САР с нечетким адаптивным регулятором напряжения.
Вектор входных переменных адаптивного нечеткого регулято-
ра |
|
|
|
(x |
, x |
|
, x |
)T , |
где x |
|
– мгновенное значение отклонения на- |
X |
i |
2i |
|
||||||||
|
|
|
1i |
|
3i |
|
1i |
|
|||
пряжения ( U Uзад |
U ); |
x2i – мгновенное значение производной |
|||||||||
отклонения напряжения (d U / dt); x3i – мгновенное значение реактивного тока статора ip БЩСГ.
207
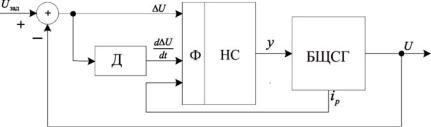
Рис. 2.35. САР с нечетким адаптивным регулятором напряжения: Д1 – дифференциатор; Ф – фаззификатор;
БЩСГ – регулируемый объект; НС – нейронная сеть
Зададимся описанием лингвистических переменных. Линейное терм-множество отклонений напряжения: отрицательное среднее (ОС), отрицательное малое (ОМ), норма (Н), положительное малое (ПМ), положительное среднее (ПС). Линейное терм-множество производной отклонения напряжения: ОС, ОМ, Н, ПМ, ПС. Линейное терм-множество реактивного тока статора: ОС, ОМ, Н, ПМ, ПС.
На рис. 2.36 приведены линейные терм-множества по отклонению напряжения, производной отклонения напряжения и реактивного тока статора, отвечающие требованиям непрерывности, непротиворечивости и полноты [8].
Исходя из динамических свойств БЩСГ задаем диапазон изменения ошибки Umin U Umax , диапазон изменения скоро-
сти изменения ошибки (d U / dt)min d U / dt (d U / dt)max , диапазон изменения реактивного тока статора (ip )min ip (ip )max . Не-
четкий адаптивный регулятор напряжения состоит из фаззификатора и НС. Фаззификатор формирует вектор степеней принадлежности терм трех лингвистических переменных регулятора: отклонение напряжения ( U ), производной отклонения напря-
жения (d U / dt) и реактивного тока статора (ip ).
208
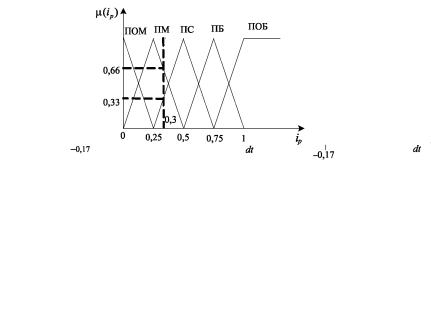
а |
б |
в
Рис. 2.36. Терм-множества регулятора напряжения
НС, показанная на рис. 2.37, состоит из входного слоя, скрытого слоя и выходного слоя.
Входной (распределительный) слой НС обрабатывает входные векторы фаззификатора по отклонению напряжения, производной отклонения напряжения и реактивному току статора. Скрытый (промежуточный) слой НС состоит из трех формальных нейронов.
Каждый нейрон скрытого слоя дополнен обратной связью. Элемент сравнения в цепи обратной связи сравнивает фактический сигнал с выхода сумматора нейрона с желаемым сигналом d (это может быть ошибка регулирования в САР или производная ошибки регулирования и т.д.). Алгоритм адаптации подстраивает коэффициенты матрицы синапсов так, чтобы свести к нулю ошибку .
209
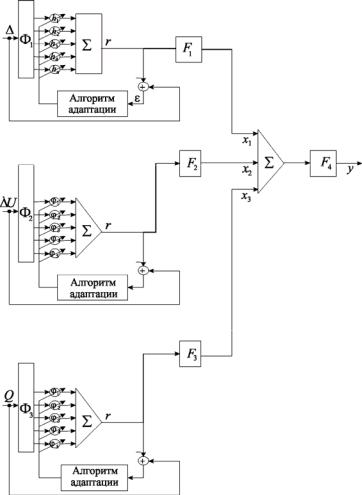
Процедурно это организуется сведением к минимуму квадрата ошибки [17].
Рис. 2.37. Адаптивный нечеткий регулятор напряжения:
F1 , F2 , F3 – активационные функции гиперболического тангенса адаптивных нейронов скрытого слоя; F4 – линейная активационная функция нейрона выходного слоя НС [10]
210
