книги / Несущая способность конструкций в условиях теплосмен

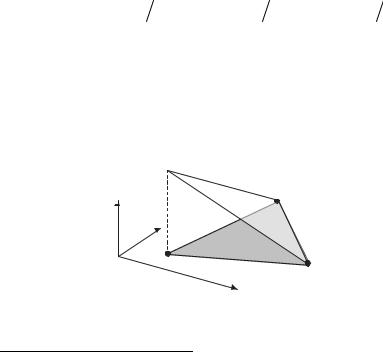
основных принципов механики (например, минимизацией потенциальной механической энергии системы, находящейся в равновесии).

Процедура формирования разрешающих соотношений рассматривается на примере решения задачи для твердого деформируемого тела, находящегося в плоско-деформированном состоянии.

Предполагается, что вершины i, j и k треугольного конечного элемента на плоскости имеют координаты {xi, yi}, {xj, yj}, {xk, yk} (рис. 13.3). Для такого конечного элемента можно определить три линейные пробные функции, или функции формы ϕi(x, y), ϕj(x, y) и ϕk(x, y). Например, функция ϕi(x, y) может быть записана в виде

ϕi (x, y ) = α i + βi x + γ i y,

где αi, βi, γi – константы, значениякоторых зависятот координатузлов:

случае, когда нумерация вершин треугольника производится в направлении, противоположном движению часовой стрелки. Особенность сконструированной ϕi(x, y) функции заключается в том, что в своем узле75 эта функция равна 1, а в двух других обращается в 0.

ϕi

x

Рис. 13.3. Кусочно-линейная пробная функция ϕi на двумерном конечном элементе

75 Иными словами, в соответствующей одноименной вершине «i» треугольного конечного элемента.

211

грузки; fx, fx – компоненты вектора массовых сил; ρ – плотность материала.

Согласно выражениям (13.1) можно получить соотношения между компонентами вектора перемещения u, v и тензора деформа-

= ui γ i + u j γ j + uk γ k + viβi + v jβ j + vk βk .

Полученные выражения записываются в матричной форме:

{ε} = [A]{u},

213

Ранее было показано, что закон Гука в случае плоскодеформированного состояния записывается в форме

С учетом предыдущего соотношения получается

{σ} = [D]{ε} = [D][A]{u}.

Подстановка этого выражения в формулу (13.2) приводит к разрешающему соотношению метода конечных элементов

[A]T [D][A]{u}dΩ ={P} + {F}.

Ω

Матрица-столбец {u} содержит числовые значения компонент вектора перемещения вершин (узлов) треугольного конечного элемента и может быть вынесена из-под знака интеграла:

В выражении (13.3) использовано обозначение матрицы жесткости конечного элемента:

[B] = [A]T [D][A]dΩ.

Ω

214

Вид записи системы линейных алгебраических уравнений (13.3), сформированной для произвольного треугольного конечного элемента, моделирующего физические свойства элементарного материального фрагмента твердого деформируемого тела, практически совпадает с выражением (12.7), полученным для произвольного стержневого элемента: в обоих случаях [B] – матрицы жесткости

вующие на фрагмент твердого деформируемого тела (балочного элемента).

13.3. Процедура ансамблирования

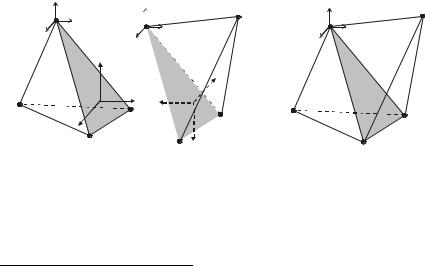
Выполняется процедура ансамблирования конечных элементов в единую композицию, аппроксимирующую всю область, занятую твердым деформируемым телом (рис. 13.4, 13.5).

Рис. 13.4. Процедура ансамблирования: аппроксимация параллелепипеда (а) с помощью набора тетраэдральных конечных элементов (б)

Формирование общей системы линейных алгебраических уравнений, позволяющей определить узловые перемещения конечных элементов, выполняется аналогично алгоритму, рассмотренному в примере реализации метода стержневых элементов. Система линейных алгебраических уравнений каждого конечного элемен-

215

та (13.3) расширяется до полной системы уравнений, содержащей все искомые узловые перемещения и все узловые нагрузки и массовые силы. Сложение всех расширенных матриц приводит к построению полной системы линейных алгебраических уравнений для всего рассматриваемого тела.

13.4. Силовые и кинематические граничные условия

Учет силовых граничных условий рассматривается на примере двух конечных элементов, имеющих общую сторону (см. рис. 13.5, а). При объединении этих конечных элементов (см. рис. 13.5, б) в единую композицию учитывается условие их механического взаимодействия76, поэтому при ансамблировании неизвестные внутренние реакции взаимодействия Fx , Fy , Fz и Fx′, Fy′, Fz′ будут исключены из

разрешающих соотношений и останутся только внешние нагрузки {P} и массовые силы {F} , действующие на рассматриваемое твер-

дое деформируемое тело.

Рис. 13.5. Конечные элементы, имеющие общую сторону (а), и ансамблирование конечных элементов в единую композицию (б)

76 Вновь используется аксиома статики, согласно которой два тела взаимодействуют с силами Fx, Fy и Fz, равными по величине и направленными в противоположные стороны (см. рис. 13.5, а).

216

Кинематические граничные условия (в перемещениях) задаются для тех вершин (узлов) конечных элементов, перемещения которых известны (например, величина осадки или сдвига) или определяются условиями симметрии, неподвижного закрепления и проч.

13.5. Реализация алгоритма метода конечных элементов

Определяется решение сформированной системы алгебраических уравнений для определения поля перемещения частиц деформируемого твердого тела.

Для решения полной системы линейных алгебраических уравнений и определения узловых компонент вектора перемещения используются прямые (Гаусса, квадратного корня) или итерационные методы (Якоби, Зейделя, простых итераций и др.).

Найденные узловые перемещения {u} вершин конечных эле-

ментов позволяют найти распределение компонент тензора деформации с помощью соотношения {ε} = [ A]{u} и далее – компоненты

тензора напряжения с использованием закона Гука {σ} = [D]{ε} во

всех конечных элементах, а значит, во всей области, занятой твердым деформируемым телом.

13.6. Анализ результатов численного решения задачи

Полученное численное решение необходимо подвергнуть критическому анализу с точки зрения достоверности полученных данных, соответствия результатов расчетов поведению реального материального объекта. Лучший способ проверки адекватности результатов вычислительного моделирования – это сопоставление результатов вычислительного моделирования с данными натурного эксперимента. Такое сравнение позволяет корректно определить погрешность вычислительной модели.

В случае невозможности проведения натурного эксперимента выполняют ряд вычислительных экспериментов на последовательности сгущающихся сеток конечных элементов. Например, первона-

217

чально выполняется вычислительный эксперимент на сравнительно грубой сетке, содержащей N конечных элементов.

Второй вычислительный эксперимент проводится с использованием конечно-элементной сетки, более точно аппроксимирующей исследуемую область и содержащей 2N конечных элементов. Очевидно, что во втором случае характерный размер конечного элемента уменьшится вдвое.

Третий вычислительный эксперимент проводится с использованием сетки, содержащей 4N конечных элементов с характерным размером, в четыре раза меньшим, чем первоначальный, и т.д.

При выполнении такой последовательности экспериментов изучаются изменения каких-то характеристик исследуемого объекта: потенциальной энергии, компонент тензоров деформации, напряжения, вектора перемещения в рассматриваемой области. Если при уменьшении характерного размера конечных элементов (увеличение числа конечных элементов) наблюдаемые параметры устанавливаются (стабилизируются), делается вывод о правильности получаемого решения.

Дополнительно может проводиться исследование устойчивости полученного решения по отношению к возмущению каких-то параметров. Например, возмущаемым параметром может быть выбран диаметр отверстия в рассматриваемом теле, наблюдаемым результатом – уровень концентрации напряжения вблизи этого отверстия. Если малое возмущение диаметра (его уменьшение или увеличение) приводит к малому изменению напряжения в зоне концентрации, решение считается устойчивым.

Дальнейшее подробное рассмотрение полученных результатов – распределение компонент вектора перемещения u и v, компонент εxx, εyy, εxy тензора деформации и σxx, σyy, σxy тензора напряжения, интенсивности деформации εi и интенсивности напряжения σi – позволяет выполнить полный анализ напряженно-деформированного состояния: выявить места концентрации деформаций и напряжений; определить области деталей узлов и конструкций, опасные с точки зрения различных теорий прочности; выявить нерационально спроекти-

218

рованные элементы конструкций, несущие чрезмерную или недостаточную нагрузку; оценить запас прочности детали, узла или агрегата при превышении допустимого значения нагрузки и проч.

13.7.Тестирование метода конечных элементов

Вкачестве тестовой задачи, как правило, используется известное точное или приближенное решение упрощенной задачи.

Рис. 13.6. Геометрическая схема осадки длинной полосы (а)

исхема кинематических граничных условий (б)

Вкачестве тестовой задачи для оценки точности алгоритма метода конечных элементов, реализованного при использовании допущения о плоско-деформированном состоянии, рассматривается задача об осадке длинной стальной полосы с квадратным поперечным сечением

размером 2×2 м2, зажатой между двумя гладкими горизонтальными плитами (рис. 13.6, а). Каждая из плит осаживается на величину . Необходимо определить, на какую величину сместятся боковые стороны этой полосы в результате деформирования. Для упрощения принимается, что массовые силы отсутствуют, то есть {F} = {0} .

Поскольку форма поперечного сечения является симметричной, можно рассматривать лишь четверть исследуемой области (рис. 13.6, б). Кинематические граничные условия указаны на этом же рисунке. Поскольку плиты, деформирующие полосу, гладкие,

219