
книги / Несущая способность конструкций в условиях теплосмен
..pdf
11.3.3. Интерполяционный полином Лагранжа
Интерполяционный полином Лагранжа строится в виде
m
Lm (x) = f (xk )ϕk (x),
k =0
то есть в каждой произвольной точке x значение полинома Лагранжа Ln (x ) определяется как линейная комбинация табличных значений
f (xk ), k = 0, m . Требование (8.1) приводит к выражению
m |
|
|
|
|
|
Lm (xi ) = f |
(xk )ϕk |
(xi ) = f (xi ), i = |
|
, |
|
0,m |
|||||
k =0 |
|
|
|
|
|
которое оказывается справедливым при выполнении условия |
|||||
ϕ |
k |
(x ) = |
0, i ≠ k, |
||
|
i |
|
|||
|
|
|
1, i = k. |
||
Это означает, что на отрезке интерполяции [a, b] каждая из |
|||||
функций ϕk (x), k = 0, m, должна иметь m корней. Каждую из функций ϕk (x ) можно записать в виде полинома
ϕk (x) = λ k (x − x0 )(x − x1 ) (x − xk −1 )(x − xk +1 ) (x − xm ),
где λk – нормировочный коэффициент, определяемый из условия
ϕk (xk ) = 1,
λ k = 1 (xk − x0 )(xk − x1 ) (xk − xk −1 )(xk − xk +1 ) (xk − xm ).
(xk − x0 )(xk − x1 ) (xk − xk −1 )(xk − xk +1 ) (xk − xm ).
С учетом полученного коэффициента λk функция ϕk (x ) записывается в форме
ϕk (x) = |
|
(x − x0 )(x − x1 ) (x − xk −1 )(x − xk +1 ) (x − xm ) |
. |
|
|
(xk − x0 )(xk − x1 ) (xk − xk −1 )(xk − xk +1 ) (xk − xm ) |
|||
|
|
|
||
В итоге полином Лагранжа можно записать в общем виде |
|
|||
Lm (x) |
= (x − x0 ) (x − xk −1 )(x − xk +1 ) (x − xm ) |
fk . |
|
|
|
|
m |
|
|
k = 0 (xk − x0 ) (xk − xk −1 )(xk − xk +1 ) (xk − xm )
151

|
|
Пример. Построить интерполяционный полином Лагранжа |
|||||||||||||||||
для функции sin х на отрезке [0, π/2]. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Значения заданной функции для указанного отрезка приведе- |
|||||||||||||||||
ны в табл. 11.7. Для каждой заданной точки xk формируются функ- |
|||||||||||||||||||
ции ϕk (x ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ϕ |
|
(x) |
= |
(x − x1 )(x − x2 )(x − x3 ) |
|
= − |
(x − π 6)(x − π 3)(x − π 2) |
; |
|||||||||||
0 |
(x0 |
|
− x1 )(x0 − x2 )(x0 − x3 ) |
|
|
|
|
π3 |
36 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ϕ |
(x) |
= |
(x − x0 )(x − x2 )(x − x3 ) |
|
= x (x − π 3)(x − π 2) |
; |
|
|
|||||||||
|
|
|
|
1 |
|
|
|
(x1 − x0 )(x1 − x2 )(x1 − x3 ) |
|
|
|
|
π 3 108 |
|
|
|
|||
|
|
ϕ |
|
(x) = |
|
(x − x0 )(x − x1 )(x − x3 ) |
= − |
x |
(x − π 6)(x − π 2) |
; |
|
||||||||
|
|
2 |
(x2 − x0 )(x2 − x1 )(x2 |
− x3 ) |
|
π3 |
108 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ϕ |
|
(x) |
= |
(x − x0 )(x − x1 )(x − x2 ) |
|
= |
x (x − π 6)(x − π 3) |
. |
|
|
|||||||
|
|
3 |
(x3 − x0 )(x3 − x1 )(x3 − x2 ) |
|
|
π3 |
36 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Окончательно полином Лагранжа принимает вид |
|
|
|
||||||||||||||
L |
|
(x) = − (x − π 6)(x − π 3)(x − π 2) 0,0 + x (x − π 3)(x − π 2) |
0,5 − |
||||||||||||||||
m |
|
|
|
|
|
|
π3 36 |
|
|
|
|
|
|
π 3 |
108 |
|
|
|
|
|
|
− x (x − π 6)(x − π 2) 0,866 025 + x(x − π 6)(x − π 3)1,0 = |
|
||||||||||||||||
|
|
|
|
|
|
|
|
π3 108 |
|
|
|
|
|
|
π3 36 |
|
|
|
|
|
|
|
|
|
|
|
= 1,74158x (x − π 3)(x − π 2) − 3,016 51x × |
|
|
|
|||||||||
|
|
|
|
|
× (x − π 6)(x − π 2) + 1,161 06x (x − π 6)(x − π 3) = |
|
|
|
|||||||||||
|
|
|
|
|
|
|
= 1,020 43x − 0,065 470 3x2 − 0,113872x3. |
|
|
|
|||||||||
|
|
Для аргумента x = π 4 построенный полином принимает зна- |
|||||||||||||||||
чение, равное 0,705 889. Точное значение этой функции в точке |
|||||||||||||||||||
x = π 4 |
|
равно |
0,707107. Относительная погрешность аппроксима- |
||||||||||||||||
ции функции |
|
sin х с помощью интерполяционного полинома Ла- |
|||||||||||||||||
гранжа составляет 0,172 %. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
152 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

11.3.4. Погрешность полинома Ньютона (Лагранжа)
Погрешность представления заданной функции f (x ) полиномом Pm (x) или полиномом Lm (x ) оценивается разностью
|
|
r (x) = f (x) − Pm (x), |
x [a,b]. |
|
|
||||||||||||||||||
Очевидно, |
|
что в |
узлах |
|
интерполяции xk , k = |
|
, погреш- |
||||||||||||||||
0, m |
|||||||||||||||||||||||
ность r (xk ) = 0 |
в силу требования (4.1). Для оценки погрешности |
||||||||||||||||||||||
в прочих точках отрезка |
[a,b] |
|
выбирается и фиксируется произ- |
||||||||||||||||||||
вольная точка x [a, b] , |
причем |
x ≠ xk , |
k = |
|
|
|
. Можно показать, |
||||||||||||||||
0, m |
|||||||||||||||||||||||
что погрешность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) − Pm (x) |
|
≤ M m+1 |
|
ω(x) |
|
(m + 1)! |
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
Здесь обозначено |
|
M |
m+1 |
= max |
|
f (m+1) (x) |
|
, f (m+1) |
(x) – произ- |
||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
водная порядка m + 1 |
функции f(x); функция ω(x) |
записывается |
|||||||||||||||||||||
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω(x) = (x − x0 )(x − x1 ) (x − xm ) .
Вчастном случае, когда функция f (x ) сама является поли-
номом степени m, Mm+1 = 0 и |
f (x) ≡ Pm (x) , то есть функция f (x ) |
|
совпадает с полиномом Ньютона. |
||
11.3.5. Сходимость процесса интерполяции полиномами |
||
Множество точек a ≤ x0 < x1 < < xm ≤ b называется сеткой |
||
на отрезке |
[a,b] и обозначается Ωm . Рассматривается последова- |
|
тельность |
Ω0 ,Ω1,Ω2 , сеток, определенных на этом отрезке, |
|
и строится |
соответствующая |
последовательность полиномов |
P0 (x), P1 (x), P2 (x), , аппроксимирующих с помощью этих сеток заданную функцию f (x ) .
153
Интерполяционный процесс сходится в точке |
x* [a,b] , если |
|||||||||
существует |
предел |
lim Pm (x* ) = f (x* ) |
(определение поточечной |
|||||||
|
|
m→∞ |
|
|
|
|
|
|
|
|
сходимости). |
|
|
|
|
|
|
|
|
|
|
Интерполяционный процесс сходится равномерно на отрезке |
||||||||||
[a,b] , если |
|
|
|
|
|
|
|
|
|
|
|
|
f − P |
= max f (x) |
− P (x) |
→0. |
|
|
|||
|
|
m |
x [a,b] |
m |
|
m→∞ |
|
|
|
|
Теорема Фабера65. Какова бы ни была последовательность се- |
||||||||||
ток Ωm , найдется непрерывная на [a,b] функция |
f |
(x ) такая, что |
||||||||
последовательность интерполяционных полиномов |
Pm (x) |
не схо- |
||||||||
дится к f (x ) равномерно на этом отрезке. |
|
|
|
|
||||||
1,4 |
|
|
|
|
|
|
|
|
|
|
1,2 |
P8 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|x| |
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
0,4 |
|
P2 |
|
|
|
|
P4 |
|
P16 |
|
0,2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
–11 |
–0,8 |
–0,6 |
–0,4 |
–0,2 |
|
|
|
|
|
|
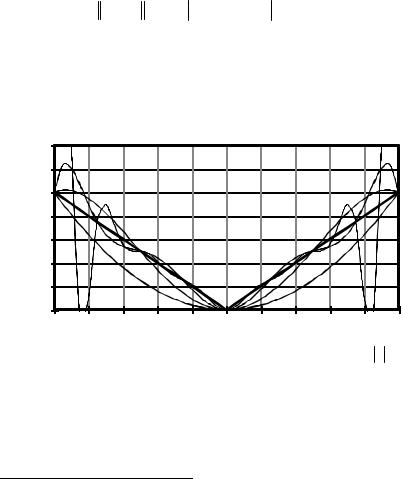
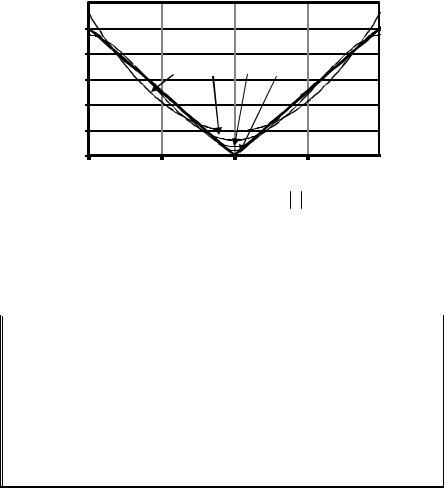
Рис. 11.9. Интерполирующие полиномы Pm для функции x
|
|
|
|
|
на равномерных сетках |
На |
|
рис. 11.9 |
приведен пример аппроксимации функции |
||
f (x) = |
|
x |
|
на отрезке |
[−1, 1] с использованием последовательности |
|
|
||||
равномерных сеток с равноотстоящими узлами. На рис. 11.10 пред-
65 Фабер Георг (05.04.1877–07.03.1966) – немецкий математик, профессор Высшей технической школы в Мюнхене.
154
ставлена погрешность аппроксимации функции f (x) = x полино-
мами Pm на равномерных сетках в зависимости от числа отрезков сеточной области.
Теорема Марцинкевича66. Если функция f (x ) непрерывна на отрезке [a,b] , то найдется такая последовательность сеток, для
которой интерполяционный процесс сходится равномерно на этом отрезке.
На рис. 11.11 приведен пример аппроксимации той же непрерывной функции f (x) = x полиномами на последовательности не-
равномерных (чебышевских67) сеток. На рис. 11.12 представлена погрешность аппроксимации этой же функции полиномами Pm на чебышевской сетке в зависимости от числа сегментов сеточной области.
δ |
|
|
|
|
|
1,E+11 |
|
|
|
|
|
1,E+07 |
|
|
|
|
|
1,E+03 |
|
|
|
|
|
Е– |
|
|
|
|
|
1,E-01 |
|
|
|
|
|
2 |
4 |
8 |
16 |
32 |
64 |
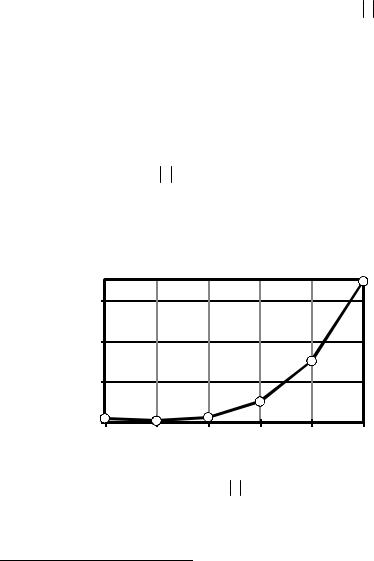
Рис. 11.10. Зависимость погрешности δ от степени m |
|||||
полинома Pm функции |
f (x) = x |
на равномерных сетках |
|||
66Марцинкевич Юзеф (30.03.1910–1940) – польский математик, профессор университета в Вильно.
67Чебышев Пафнутий Львович (04.05.1821–26.11.1894) – русский ученыйматематик, доцент, профессор Петербургского университета, академик Петербургской академии наук.
155
1,4 |
|
|
|
|
|
1,2 |
|
|
|
|
|
1,0 |
|
|
|
|
|
0,8 |
|
|
|
|
|
0,6 |
|
P8 |
P4 |
P2 |
|
0,4 |
|
|
|||
|
P16 |
|
|
|
|
|
|
|
|
|
|
0,2 |
|
| |
x| |
|
|
|
|
|
|
||
0,0 |
|
|
|
|
|
–1,0 |
–0,5 |
0,0 |
0,5 |
|
1,0 |
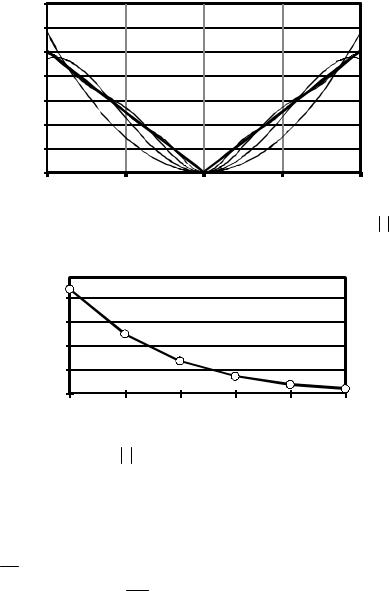
Рис. 11.11. Интерполяционные полиномы Pm для функции |
f (x) = x |
||||
|
на неравномерных (чебышевских) сетках |
|
|
||
δ |
|
|
|
|
|
0,2 |
|
|
|
|
|
0,15 |
|
|
|
|
|
0,1 |
|
|
|
|
|
0,05 |
|
|
|
|
|
0 |
|
|
|
|
|
2 |
4 |
8 |
16 |
32 |
64 |
Рис. 11.12. Зависимость погрешности δ от степени m полинома Pm |
|||||
функции |
f (x) = x |
на неравномерных (чебышевских) сетках |
|||
11.3.6.Метод наименьших квадратов
Впрактических исследования часто возникает ситуация, когда
необходимо аппроксимировать табличные значения fi = f (xi ), i = 0,n , с помощью приближения ϕ(x), содержащего определяемые коэффициенты ak , k = 0, m , в количестве, меньшем, чем число узловых точек, – m < n.
156
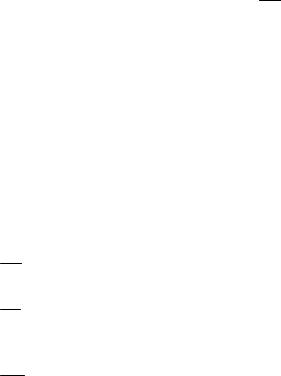
По этой причине, в отличие от рассмотренных ранее способов аппроксимации функции полиномами Ньютона и Лагранжа, не используется условие равенства значений функции f(x) и ее приближения ϕ(x) в узлах xi разностной сетки.
В методе наименьших квадратов близость аппроксимирующего многочлена заданной функции оценивается в среднем, то есть в целом для всего отрезка, на котором строится аппроксимация.
Пусть известен набор значений fi = f (xi ), i = 0, m , функции
для некоторых значений ее аргумента. Отыскиваемое приближение ϕ (x ) зависит от известного числа m +1 параметров a0 , a1, , am .
Степень отклонения заданных значений функции f(xi) от приближенных значений ϕ(xi) определяется выражением
δ = |
n |
f |
i |
− ϕ(x |
i |
) 2 |
= |
n |
f 2 |
− 2 |
n |
f |
ϕ(x |
) + |
n |
ϕ2 (x |
). |
|
|
|
|
|
i |
|
i |
i |
|
|
i |
|
|||||
|
i=0 |
|
|
|
|
|
|
i=0 |
|
|
i=0 |
|
|
|
i=0 |
|
|
Для определения наименьшего отклонения δ используются необходимые условия минимума функции нескольких переменных:
∂δ
∂a0∂δ
∂a1
∂δ∂am
n
=−2 fi
i=0 n
=−2 fi
i=0
n
=−2 fi
i=0
|
∂ϕ(xi ) |
n |
|
|
∂ϕ(xi ) |
|
||||||
|
|
|
|
|
+ 2ϕ ϕ(xi |
) |
|
|
|
|
= 0; |
|
|
|
∂a0 |
∂a0 |
|
||||||||
|
|
i=0 |
|
|
|
|
||||||
∂ϕ(xi ) |
n |
∂ϕ(xi |
) |
|
|
|
||||||
|
|
|
|
|
+ 2 ϕ(xi ) |
|
|
|
|
|
= 0; |
|
|
|
∂a1 |
|
|
∂a1 |
|
|
|||||
|
|
i=0 |
|
|
|
|
|
|
||||
|
|
∂ϕ(xi ) |
n |
|
∂ϕ(xi ) |
|
|
|||||
|
|
|
|
|
+ 2 ϕ(xi ) |
|
|
|
|
= 0. |
||
|
|
∂am |
|
∂am |
|
|
||||||
|
|
i=0 |
|
|
|
|
|
|
||||
Иными словами, речь идет о решении системы алгебраических уравнений, нелинейных в общем случае:
157

|
|
( fi − ϕ(xi )) ∂ϕ(xi ) = 0; |
|
|
|||||
|
|
|
n |
|
|
|
|
|
|
|
|
i=0 |
|
∂a0 |
|
|
|
||
|
|
|
n |
|
∂ϕ(xi ) |
|
|
|
|
|
|
( fi − ϕ(xi |
)) |
= 0; |
|
|
|||
|
|
|
|
|
|||||
|
|
i=0 |
|
|
∂a1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ϕ(xi ) |
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
( fi − ϕ(xi |
)) |
= 0. |
|
|
|||
|
|
|
|
|
|||||
|
|
i=0 |
|
∂am |
|
|
|||
В частном случае, когда приближение ϕ(x) представимо в виде |
|||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
ϕ(x) = ak ϕk (x), |
|
|
||||
|
|
|
k =0 |
|
|
|
|
|
|
оценка отклонения функции от |
ее |
приближения |
записывается |
||||||
в форме |
|
|
|
|
|
|
|
|
|
n |
|
n |
m |
n |
m |
m |
|
||
δ = fi |
2 |
− 2 fi ak ϕk (xi ) + |
ak ϕk (xi ) ajϕ j (xi ) . |
||||||
i=0 |
|
i=0 |
k =0 |
i=0 |
k =0 |
j=0 |
|
||
Условие минимальности отклонения приближения от функции записывается аналогично представленному выше:
∂δ
∂a0
∂δ∂a1
∂δ
∂am
= −2 fi ϕ0 |
(xi ) + 2 ϕ0 |
(xi ) ak ϕk (xi ) = 0; |
||
n |
n |
|
m |
|
i=0 |
i=0 |
|
k =0 |
|
= −2 fi ϕ1 |
(xi ) + 2 ϕ1 |
(xi ) ak ϕk (xi ) = 0; |
||
n |
n |
|
m |
|
i=0 |
i=0 |
|
k =0 |
|
= −2 fi ϕm (xi ) + 2 ϕm (xi ) ak ϕk (xi ) |
= 0. |
|||
n |
n |
m |
|
|
i=0 |
i=0 |
k =0 |
|
|
В итоге получена система линейных алгебраических уравнений относительно коэффициентов разложения ak , k = 0, m :
158
|
n |
n |
|
n |
|
n |
|
|
a0 ϕ0 |
(xi )ϕ0 (xi ) + a1 ϕ1 |
(xi )ϕ0 |
(xi ) + + am ϕm (xi )ϕ0 |
(xi ) = fiϕ0 |
(xi ); |
|||
|
i=0 |
i=0 |
|
i=0 |
|
i=0 |
|
|
|
n |
n |
(xi )ϕ1 |
n |
|
n |
(xi ); |
|
a0 ϕ0 |
(xi )ϕ1 (xi ) + a1 ϕ1 |
(xi ) + + am ϕm (xi )ϕ1 |
(xi ) = fiϕ1 |
|||||
|
i=0 |
i=0 |
|
i=0 |
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
n |
|
n |
|
|
a0 ϕ0 |
(xi )ϕm (xi ) + a1 ϕ1 (xi )ϕm (xi ) + + am ϕm (xi )ϕm (xi ) = fiϕm (xi ). |
|||||||
|
i=0 |
i=0 |
|
i=0 |
|
i=0 |
|
|
Pm |
|
|
|
|
|
1 |
|
|
|
|
|
0,8 |
P2 |
P3 |
P4 |
P5 |
|
0,6 |
|
||||
|
|
|
|
|
|
0,4 |
|
|
|
|
|
0,2 |
|
|
|
|
|
0 |
|
|
| x| |
|
|
|
|
|
|
x |
|
–1,0 |
–0,5 |
0,0 |
|
0,5 |
Рис. 11.13. Приближение функции f (x) = x полиномами Pm, построенными методом наименьших квадратов
На |
|
рис. 11.13 показан |
пример |
приближения |
функции |
|||
f (x) = |
|
x |
|
полиномами Pm, построенными на отрезке [–1, 1] с ис- |
||||
|
|
|||||||
пользованием метода наименьших квадратов. |
|
|
||||||
|
|
|||||||
Пример. Аппроксимировать с помощью линейной зависимо- |
|
|||||||
сти ϕ (x ) = a0 + a1 x функцию |
f (x) = x2 , |
заданную с |
помощью |
|||||
табл. 11.9, методом наименьших квадратов.
Для рассматриваемой задачи определяется величина отклонения заданных значений fi от значений, определяемых функцией
ϕ (xi ) = a0 + a1 xi :
δ = |
4 |
|
− (a + a x |
|
) 2 |
f |
i |
i |
|||
|
|
0 1 |
|
||
|
i=0 |
|
|
|
|
4 |
|
4 |
4 |
= fi |
2 |
− 2 fi (a0 + a1x i ) + (a0 + a1x i )2 . |
|
i=0 |
|
i=0 |
i=0 |
159

|
|
|
Таблица 11.9 |
|
Табличные значения фукции |
f (x) = x2 |
|
№ п/п |
xi |
|
f(xi) |
1 |
0 |
|
0 |
2 |
1/4 |
|
1/16 |
3 |
1/2 |
|
1/4 |
4 |
3/4 |
|
9/16 |
5 |
1 |
|
1 |
С помощью необходимых условий минимума функции двух переменных
∂δ
∂a0∂δ
∂a1
44
=−2 fi + 2 (a0 + a1xi ) = 0;
i=0 i=0
nn
=−2 fi xi + 2 (a0 + a1xi ) xi = 0
i=0 i=0
получается система линейных алгебраических уравнений относительно коэффициентов разложения ak , k = 0, m , для определения наименьшего отклонения δ:
(a0 + a1xi ) = fi , |
||||
|
4 |
|
|
4 |
i=0 |
|
|
i=0 |
|
|
n |
|
|
n |
(a0 + a1xi ) xi |
|
= fi xi ; |
||
i=0 |
|
|
i=0 |
|
|
4 |
|
4 |
|
4a0 + a1 xi = fi , |
||||
|
i=0 |
i=0 |
||
|
n |
n |
|
n |
|
|
2 |
= fi xi . |
|
a0 xi + a1 |
xi |
|
||
|
i=0 |
i=0 |
|
i=0 |
Использование данных табл. 11.9 приводит к системе линейных алгебраических уравнений
160
