книги / Принципы и практика решения задач по общей физике. Оптика. Квантовая физика

В силу уравнения непрерывности должно выполняться равенство

R + D =1,

так как сумма вероятностей отражения частицы от барьера и его прохождения должна быть равна единице (частица не может исчезнуть в никуда!).

4.2.1. Прямоугольный потенциальный барьер. На пути дви-

жения частицы с энергией E находится бесконечно протяженный прямоугольный потенциальный барьер высотой U0 (рис. 4.6). Иссле-

частица отразится от барьера и полетит обратно. Для того чтобы это понять, обратимся к стационарному уравнению Шредингера. В области x < 0, где U = 0, оно имеет вид

211

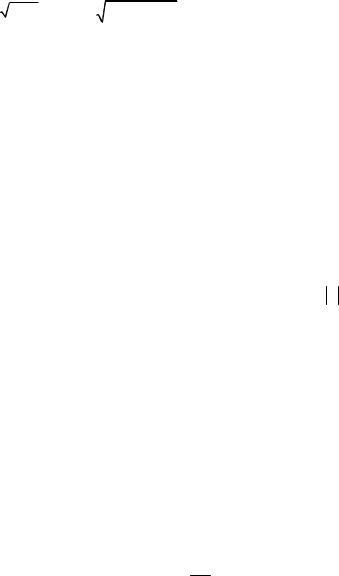
где k1 = 2mE / ; k2 = 2m(E −U0 ) / ; постоянные a, b – амплитуды этих волн. Характер принятых нами решений уже предполагает возможность движения частицы, как вдоль оси x ( exp(ikx)), так

и против нее exp(−ikx), т.е. предполагает возможность отражения

частицы от барьера! Вероятность отражения (и соответственно прохождения) определяется амплитудами соответствующих волн. Для их определения нам необходимо учесть условия непрерывности и гладкости решений в точке разрыва потенциальной энергии. Но этих условий в точке x = 0 только два, а неизвестных амплитуд четыре. Поэтому нам потребуются некоторые физические предположения о характере движения частицы. Так как в области x > 0 неоткуда взяться волне, бегущей против оси x (частица двигается на барьер слева направо), то следует положить b2 = 0. Кроме того, сама волно-

∞

вая функция должна подчиняться условию нормировки ∫ ψ 2dx =1.

−∞

Но это условие для неограниченного движения оказывается невозможным, так как такой интеграл расходится. Поэтому в данной ситуации имеет смысл не квадрат модуля волновой функции, а отношение квадратов модулей волновых функций, взятых в разных точках пространства. Это отношение дает относительную вероятность обнаружения частицы в разных точках пространства. Таким образом, нам необходимо рассматривать либо отношение амплитуды волн к амплитуде падающей волны, либо принять амплитуду падающей волны за единицу. Выберем второй вариант. Тогда выражения (1) принимают вид

ψ1 (x < 0) = exp(ik1x) +b1 exp(−ik1x), ψ2 (x > 0) = a2 exp(ik2 x).

Из условий непрерывности ψ и ddxψ в точке x = 0 следует, что коэффициенты b1 и a2 определяются из системы уравнений

212

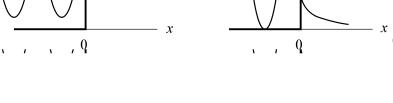
1+b1 = a2 , k1 −b1k1 = a2k2.

Откуда находим

Значения этих постоянных определяют амплитуду отраженной от барьера волны (b1 ) и амплитуду прошедшей волны (a2 ). Непосред-

ственный же физический смысл имеет квадрат модуля волновой функции – он определяет плотность вероятности обнаружения частицы в соответствующей точке пространства P(x). Найдем ее:

Откуда с учетом формулы Эйлера exp(ix) = cos x +isin x получаем

P(x < 0) = (1+b1 )2 −4b1 sin2 k1x.

Аналогично

P(x ≥ 0) = ψ2ψ2 = a22 = (1+b1 )2 ,

где значения b1 и a2 даются выражением (2). Соответствующие графики приведены на рис. 4.7, а.

Рис. 4.7

213

Вероятность отражения частицы от барьера – коэффициент отражения R – в соответствии с введением в данный раздел можно определить как отношение плотности потока вероятности отраженной

от барьера волны j′ kψψ k1b12 к плотности потока вероятности падающей волны j k1:

R = b2 = k1 −k2 2 .

1 k1 +k2

Соответственно коэффициент прохождения

Видно, что значения R и D не зависят о направления движения частицы (параметры k1 и k2 входят симметрично). Кроме того, вероятность отражения обращается в нуль только при k1 = k2 , т.е. при

U0 = 0 (в «классике» R = 0 при любых E >U0 ).

Обратимся теперь к случаю E <U0. Теперь величина k2 стано-

вится чисто мнимой и решения уравнения Шредингера принимают вид

ψ1 (x < 0) = a1 exp(ik1x) +b1 exp(−ik1x),

ψ2 (x > 0) = a2 exp(βx) +b2 exp(−βx),

где β = ik2 = 2m(U0 − E) / . Как и ранее, полагаем a1 =1. Кроме того, так как решение не должно расходиться при больших x, теперь необходимо полагать a2 = 0. Таким образом, для волновых функций имеем

ψ1 (x < 0) = exp(ik1x) +b1 exp(−ik1x),

ψ2 (x > 0) = b2 exp(−βx).

214

215

Это означает, что отражение является полным. Но при этом ψ-функ- ция в области барьера не обращается в нуль в каждой точке. Ее значение

ψ2 (x > 0) = k12+k1iβexp(−βx)

стремится к нулю только экспоненциально. Это означает, что плотность вероятности обнаружения частицы в области барьера

P(x) = ψ2 2 = 4E exp(−2βx)

U0

с увеличением глубины проникновения также убывает экспоненциально. И это убывание происходит тем быстрее, чем больше разность U0 − E. Обычно глубину проникновения определяют как расстоя-

ние l, на котором P(x) убывает в e раз. При этом 2βl =1 и

Таким образом, несмотря на полное отражение, частица все же проникает на небольшое расстояние в область барьера. С точки зрения классической механики это запрещено, так как полная энергия не может быть меньше потенциальной (становится отрицательной кинетическая энергия). В квантовой же механике деление энергии на кинетическую и потенциальную не имеет смысла, так как невозможно знать их точно одновременно. Потенциальная энергия – функция координат, а кинетическая – функция импульса. А координату и импульс нельзя измерить точно одновременно в силу принципа неопределенности. Поэтому заключение об отрицательности кинетической энергии частицы внутри барьера также становится бессмысленным.

4.2.2. Барьер конечной ширины. Пусть теперь потенциальный барьер имеет конечную ширину l (рис. 4.8). Мы не будем ставить задачу полного исследования характера движения частицы, найдем только коэффициент прохождения D.

216

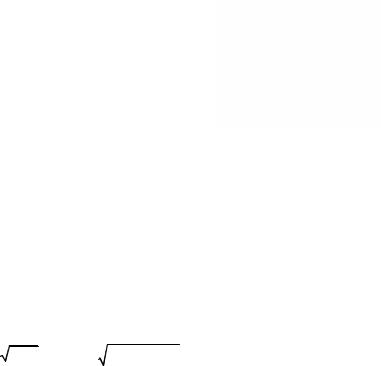
Рассмотрим вначале случай E >U0.

В соответствии с общей идеологией нам требуется решить уравнение Шредингера для трех областей:

условие непрерывности волновых функций и их гладкости в точках x = 0 и x = l

ψ1 (0) = ψ2 (0), ψ1′(0) = ψ′2 (0),

ψ2 (l ) = ψ3 (l ), ψ′2 (l) = ψ′3 (l ).

Сучетом этих условий приходим к неоднородной системе линейных уравнений относительно величин b1, a2 , b2 , a3:

217

Так как мы ставим своей целью нахождение только коэффициента прохождения, определяемого как D = a3 2 , то нам из всей системы уравнений необходимо найти только величину a3. Поэтому разумно воспользоваться методом Крамера (методом определителей). В соответствии с этим методом a3 = ∆3 / ∆, где ∆ – определитель матрицы, составленной из коэффициентов системы уравнений (2) при неизвестных b1, a2 , b2 , a3:

=(k1 +k2 )2 exp(−ik2l ) −(k1 −k2 )2 exp(ik2l) exp(ik1l ),

а∆3 определяется как

218

Тогда после несложных преобразований с учетом формулы Эйлера имеем

Заметим, что если бы частица проходила не над барьером высотой U0 , а над потенциальной ямой глубиной U0 (рис. 4.9), то коэффициент прозрачности можно определять по этой же формуле с заменой U0 → −U0

Из выражения (3) следует, что частица с энергией большей высоты потенциального барьера может пройти над ним беспрепятственно (D =1) при условии sin k2l = 0. Это может быть выполнено,

если k2l = nπ(n =1,2,3...). Данное условие можно интерпретировать как l = nλ/ 2, где λ – дебройлевская длина волны частицы в области над барьером (ямой). При этом значение энергии частицы

Рассмотрим теперь случай, когда полная энергия частицы меньше высоты потенциального барьера. Теперь величина

k2 = 2m(E −U0 ) / становится чисто мнимой и сейчас удобно ввести новый параметр β = ik2. Тогда вместо (1) мы имеем

ψ1 = a1 exp(ik1x) +b1 exp(−ik1x),

ψ2 = a2 exp(βx) +b2 exp(−βx),

219

ψ3 = a3 exp(ik1x) +b3 exp(−ik1x).

Понятно, что нам не следует повторять весь пройденный ранее путь для определения коэффициента прохождения D. Необходимо

Для практически важных случаев величина βl = l 2m(U0 − E) /

много больше единицы. В этом случае sh (βl ) ≈ exp(βl )/ 2 >>1 и тогда, пренебрегая единицей в квадратных скобках, имеем

диться, его максимальное значение равно 4, т.е. составляет величину

220