книги / Принципы и практика решения задач по общей физике. Оптика. Квантовая физика

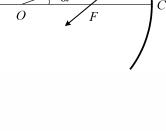
1.2. Отражение и преломление света на сферической поверхности. Линзы

Естественно, отражение и преломление света на любой криволинейной поверхности подчиняется уже известным нам законам. В то же время на практике наиболее часто встречаются случаи отражения и преломления именно на сферической поверхности. Важнейшие из оптических инструментов или их составные части относятся к так называемым центрированным оптическим системам. Они представляют собой оптически однородные преломляющие или отражающие среды, отделенные одна от другой сферическими поверхностями, центры кривизны которых расположены на одной прямой – главная оптическая ось. Обычно, если это не может привести к недоразумениям, прилагательное «главная» будем опускать. Поэтому есть смысл иметь готовые выражения, связывающие положение предмета и его изображения с радиусом кривизны сферической поверхности и свойствами сред.

Начнем с отражения света и будем рассматривать только параксиальные лучи. С практической точки зрения это означает, что размеры зеркала малы по сравнению с его радиусом кривизны R. Рассмотрим какой-либо луч, падающий на вогнутое зеркало параллельно главной оптической оси OC (рис. 1.16, O – центр кривизны сферической поверхности). После отражения в точке B луч пересечет оптическую ось в точке F.

Так как угол падения α мал, то OF = FB ≈ FC. Отсюда сразу следует вывод о том, что при малых углах падения лучей, параллельных оптической оси, все отраженные лучи независимо от угла падения пересекают оптическую ось в одной и той же точке F (фокус зеркала), находящейся на половине радиуса кривизны. Таким образом, фокусное расстояние сферического зеркала

21

Если же на зеркало падает параллельный пучок лучей под небольшим углом к оптической оси, то после отражения он соберется в фокальной плоскости, перпендикулярной оптической оси и проходящей через фокус зеркала.

Пусть теперь источник света находится на оптической оси в некоторой точке S на расстоянии a от зеркала между фокусом и центром кривизны O (рис. 1.17). Отраженный луч пересечет оптическую ось в некоторой точке S′, которую можно считать изображением точки S, так как саму оптическую ось

Следовательно,

γ+θ = 2β.

Иесли полагать все углы малыми, то с учетом того, что угол равен отношению дуги к радиусу, из последнего равенства следует

Из (2) следует, что расстояние от изображения до зеркала не зависит от угла γ, т.е. все лучи, исходящие от предмета, после

22

и после отражения от зеркала он пройдет через фокус. Луч 2 проходит через фокус, поэтому после отражения он пойдет параллельно оптической оси. И, наконец, луч 3 можно послать через центр кривизны зеркала и после отражения он вернется обратно по тому же пути. Точка пересечения S′ всех этих лучей и есть изображение точки S.

Аналогичным образом строятся изображения, если точка S находится за центром кривизны зеркала (рис. 1.19, а) и между зеркалом и фокусом (рис. 1.19, б). В первом случае (см. рис. 1.19, а) изображение (S′) получается на пересечении лучей и является действитель-

ным, во втором (см. рис. 1.19, б) – на пересечении продолжения лучей, т.е. является мнимым.

Рис. 1.19

23

Для всех рассмотренных случаев положения предмета формула зеркала (2) остается справедливой, если ввести правило знаков: если изображение находится с отражающей стороны зеркала (на всех рисунках слева от зеркала), то расстояние b до изображения считается положительным; если же

за зеркалом – то отрицательным (мнимое изображение). Более то-

го, формула (2) работает и для выпуклого зеркала. На рис. 1.20 приведено построение изображения предмета в виде стрелки в выпуклом зеркале. При этом независимо от положения предмета, его изображение является всегда мнимым (расстояние b < 0). Кроме того, необхо-

димо считать, что радиус кривизны R, а значит, и фокусное расстояние f также отрицательны.

Рассмотрим теперь преломление света на сферической поверхности раздела двух прозрачных сред. Пусть источник света S находится в среде с показателем преломления n1 и лучи, исходящие от него, по-

падают в среду с показателем преломления n2 (рис. 1.21). Радиус кривизны преломляющей поверхности CO = R. Исходящий от источника под малым углом γ к оптической оси луч после преломления

Рис. 1.21

24

пересечет оптическую ось в точке S′, являющейся изображением точки S. По закону преломления

n1 sin α = n2 sinβ.

Так как мы рассматриваем только параксиальные лучи, то последнее равенство приобретает вид

Отсюда видно, что при заданной величине a расстояние до изображения b не зависит от угла γ, следовательно, все лучи, исходя-

щие из точки S, после преломления соберутся в точке S′. Уравнение (4) справедливо и для вогнутой преломляющей поверхности, если ввести правила знаков:

1.Для выпуклой преломляющей поверхности радиус кривизны положителен, а для вогнутой – отрицателен.

2.Расстояние до изображения b положительно, если источник

света и изображение находятся по разные стороны от преломляющей поверхности (действительное изображение), и отрицательно,

25

если источник света и изображение находятся по одну сторону от преломляющей поверхности (мнимое изображение).

3. Расстояние до предмета a положительно, если предмет действительный, и отрицательно, если предмет мнимый. Этот случай может иметь место, когда сам предмет является изображением, полученным от какой-либо линзы или зеркала, при этом лучи на преломляющую поверхность идут сходящимся пучком.

Применяя последовательно выражение (4) для двух сферических поверхностей (случай линзы), можно получить формулу тонкой линзы. Однако для лучшего понимания физической природы формирования изображения в тонкой линзе мы получим данную формулу, исходя из принципа таутохронизма. Пусть S точечный источник света, расположенный на главной оптической оси линзы, а S′ – его изображение (рис. 1.22). Согласно принципу таутохронизма, оптические длины всех лучей, вышедших из S и собравшихся в S′, одинаковы. Опишем из S и S′, как из центров, окружности с радиусами SA и S′B соответственно.

Рис. 1.22

На основании равенства оптических длин лучей можем записать

(CED) =( AB),

26

где круглые скобки обозначают оптические длины лучей, заключенных в эти скобки. Если лучи SE и ES′ параксиальные, то можно принять, что длина ломаной CED приближенно равна длине ее проекции MN на главную оптическую ось. В этом приближении предыдущее соотношение можно записать в виде

где R1 и R2 – радиусы кривизны сферических поверхностей линзы.

Аналогично, при выполнении условия параксиальности справедливы выражения

AM = (EL2a)2 , BN = (EL2b)2 ,

где a и b обозначают соответственно длины SA и BS′. Подставляя написанные выражения в формулу (5), получим так называемое уравнение шлифовщика линз:

кусное расстояние f . Поэтому, если источник удалить в бесконечность (a →∞), то величина b совпадет с фокусным расстоянием f и тогда уравнение (6) приобретает вид

27

или

Если же на линзу падает параллельный пучок лучей под небольшим углом к главной оптической оси, то он соберется в фокальной плоскости, перпендикулярной оптической оси и проходящей через фокус линзы.

Уравнение тонкой линзы (7) ничем не отличается от уравнения зеркала (2). Для того чтобы полученными выражениями можно было пользоваться в случае любых тонких линз (собирающих и рассеивающих) и при любом положении предмета и его изображения, примем для определенности следующие правила знаков:

1.Фокусное расстояние положительно для собирающих линз

иотрицательно для рассеивающих.

2. Для выпуклой преломляющей поверхности радиус кривизны положителен, а для вогнутой – отрицателен.

3. Расстояние до изображения b положительно, если источник света и изображение находятся по разные стороны от преломляющей поверхности (действительное изображение), и отрицательно, если источник света и изображение находятся по одну сторону от преломляющей поверхности (мнимое изображение).

4. Расстояние до предмета a положительно, если предмет действительный, и отрицательно, если предмет мнимый. Этот случай может иметь место, когда сам предмет является изображением, полученным от какой-либо линзы или зеркала, при этом лучи на преломляющую поверхность идут сходящимся пучком.

Мы получили формулу тонкой линзы, исходя из предположения о том, что оптические длины всех путей, которыми свет приходит из одной точки в другую, одинаковы. На самом деле распространение света подчиняется волновым законам. Наиболее явно волновые свойства света проявляются в его интерференции и дифракции. И именно благодаря интерференции волн, прошедших одинаковые оптические пути, и возникает усиление волн, приводящее к формированию оптического изображения.

28

щейся на главной оптической оси, достаточно воспользоваться двумя из каких-либо трех лучей (рис. 1.24): луч 1 па-

раллелен главной оптической оси, поэтому после преломления в линзе он пройдет через фокус за линзой, если линза собирающая (см. рис. 1.24), или будет отклоняться от главной оптической оси так, как будто он выходит из фокуса перед линзой, если линза рассеивающая (рис. 1.25); луч 2 проходит через центр линзы, не отклоняясь (здесь обе поверхности практически параллельны). И, наконец, луч 3 в случае собирающей линзы идет через фокус, расположенный по ту же сторону от линзы, что и точка S, поэтому в результате преломления он оказывается параллельным главной оптической оси; в случае,

Рис. 1.24

Рис. 1.25

29

если линза рассеивающая, луч 3 идет в направлении фокуса, расположенного за линзой, и также после преломления становится параллельным главной оптической оси. Если любые два из этих лучей пересекаются в некоторой точке S′, то изображение будет действительным, если же пересекаются их продолжения, то изображение будет мнимым.

Как видно на рис. 1.24 и 1.25, действительное изображение может быть получено только собирающей линзой, если предмет находится за фокусом, при этом изображение перевернутое. Если же предмет расположен между фокусом и линзой или линза рассеивающая, то изображение будет мнимым и прямым.

1.2.1. Параболическое зеркало. Ранее нами было показано,

что при отражении параллельного оптической оси сферического зеркала пучка света он собирается в фокусе, только если пучок узкий. При расширении пучка точка схождения отраженных лучей приближается к вершине зеркала. В связи с этим возникает вопрос: какова должна быть форма отражающей поверхности, чтобы параллельный пучок света любой ширины собирался строго в одной точке?

Нетрудно понять, что смещение точки схождения лучей при отражении от сферического зеркала связано с постоянством радиуса кривизны зеркала. Поэтому необходимо поискать такую поверхность, радиус кривизны которой возрастал бы с удалением от вершины зеркала. Одной из таких поверхностей является параболоид вращения, сечение которого плоскостью, проходящей через его ось, представляет параболу. Проверим наше предположение.

Одно из определений параболы говорит, что данная кривая является геометрическим местом точек M (x, y), равноудаленных

(рис. 1.26, а) от данной точки F (фокуса) и от данной прямой NN′ (директрисы), т.е. MF = KM . Директриса проходит перпендикулярно оси параболы на расстоянии p / 2 от вершины параболы по другую сторону от фокуса. На таком же расстоянии от вершины p / 2 находится и фокус параболы F. Величина p называется фокальным па-

30