
книги / Математическое моделирование кинетики сложных химических реакций. Ч. 1
.pdfВозведем в квадрат равенство (4.34) и, преобразовав, получим
dy1 |
2 |
1 |
(c1 |
+c2 |
2 |
)(c2 |
2 |
). |
(4.35) |
||
|
dx |
|
= |
2 |
−2y1 |
−2c1 + y1 |
|||||
|
|
|
|
|
|
|
|
|
|
||
Для уравнения (4.35) введем следующие обозначения
c1 +c2 = a,c2 −2c 1=b.
С учетом введенных обозначений уравнение (4.35) запишется как
( y′)2 |
= y4 |
− |
a |
+b |
y2 |
+ ab . |
(4.36) |
||
1 |
1 |
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
Если теперь ввести ещё дополнительные обозначения
|
a |
|
= A, |
|
|
− |
2 |
+b |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ab |
= B, |
|
|
||
|
2 |
|
|
||
|
|
|
|
|
|
то равенство (4.36) можно записать кратко |
|
||||
( y1′)2 = y14 + Ay12 + B. |
(4.37) |
||||
Выражение (4.37) есть нелинейное дифференциальное уравнение специального типа, которое сводится специальными математическими построениями к эллиптическим функциям (см. п. Д. 2.6). Техника таких построений приводится в п. 4.4.4.
Остановимся пока на частных случаях полученного уравнения (4.35). Перепишем его так:
dy1 |
2 |
a |
2 |
|
2 |
). |
||
|
dx |
|
= |
2 |
− y1 |
|
(b − y1 |
|
|
|
|
|
|
|
|
||
151

Пусть |
a |
= b, тогда можно записать |
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dy1 |
2 |
2 |
) |
2 |
или |
dy1 |
2 |
), |
(4.38) |
|
|
|
dx |
|
=(b − y1 |
|
dx |
= ±(b − y1 |
||||
|
|
|
|
|
|
|
|
|
|
||
и уравнение распадается на два уравнения (случай кратных корней):
dy1 |
=b − y2 |
, |
(4.39) |
|
dx |
|
1 |
|
|
|
|
|
|
|
dy1 |
= y2 |
−b. |
(4.40) |
|
dx |
1 |
|
|
|
|
|
|
|
|
Решаем сначала уравнение (4.39):
∫ ydy2 −1 b = −∫ dx +c3′
1
(интеграл типа ∫ u2du−a2 = 21a ln uu +−aa +c* ).
Отсюда |
|
1 |
ln |
y1 |
− |
b |
= −x +c′. |
|
|
|
|
|
|
|
|||
2 |
b |
|
y1 |
+ |
b |
3 |
||
|
|
|||||||
Выразим y1:
y1 = |
1 |
+c e−2 |
bx |
|
|
|
3 |
|
, |
(4.41) |
|
1 |
−c e−2 |
bx |
|||
|
|
3 |
|
|
|
где c3 = ec3′ 2 b .
Функция y1 будет существовать при условии, что
1−c e−2 bx ≠ 0, отсюда |
c e−2 bx ≠1. |
3 |
3 |
С учетом введенного обозначения b = c2 −2c1 окончательно получим
y1 |
= |
1+c3e |
−2 c2 |
−2c1x |
. |
(4.42) |
|||
|
|
|
|||||||
|
|
|
|
|
|||||
1−c3e |
−2 |
c2 |
−2c1x |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
152
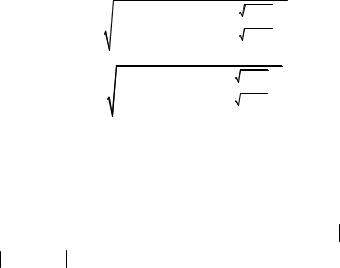
Исследуем теперь предельные случаи выражения (4.42):
|
|
= |
1+c e0 |
= |
1+c |
= c* = const, |
||
lim y |
|
|
3 |
|
3 |
|||
|
1−c3e0 |
1−c3 |
||||||
x→0 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
(4.43) |
lim y |
=1 |
+0 |
=1. |
|
|
|||
x→+∞ |
1 |
1 |
−0 |
|
|
|
|
|
Здесь c* – есть некоторая первоначальная постоянная для концентрации вещества C1. Попутно заметим, что если c2 −2c1 > 0, то функция y1 является функцией действительного переменного x, если c2 −2c1 < 0 – функцией комплексного переменного x.
Найденное по формуле (4.42) значение y1 подставим в (4.32) и (4.33) и получим окончательные выражения для y2 и y3:
y2 = |
c |
− |
2c |
+ |
1 |
|
1 |
+c e−2 c2 |
−2c1x |
|
||||||||||
2 |
1 |
|
|
|
|
|
|
3 |
|
|
|
, |
(4.44) |
|||||||
|
|
|
|
|
|
|
|
−c e−2 c2 |
|
|
||||||||||
|
3 |
|
3 |
|
|
|
3 |
|
1 |
−2c1x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
c c |
|
1 |
|
1 |
+c e−2 c2 |
−2c1x |
|
||||||||||||
y = |
1 |
+ |
2 |
|
− |
|
|
|
|
|
|
|
|
3 |
|
|
. |
(4.45) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
6 6 3 |
|
1 |
−c e−2 c2 |
−2c1x |
|
||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
Аналогично решается второе уравнение (4.40). Его решения имеют такой же вид, как и (4.42), (4.44) и (4.45), но отличаются только знаками.
Из общих решений (4.42). (4.44) и (4.45) выделим какиелибо частные решения системы (4.26). Для этого решим задачу
Коши, например, при таких начальных условиях: y1 x=0 =1;
y2 x=0 =1; y3 x=0 =1.
Подставив их в выражения (4.42). (4.44) и (4.45), получим систему для определения c1, c2 и c3.
153
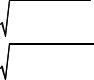
|
= |
1 |
+с3 |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
, |
|
|
|
|
|
|
|
1 |
−с3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
= |
|
|
1 |
c2 |
− |
2 |
c1 |
+ |
1 |
, |
(4.46) |
1 |
|
|
3 |
3 |
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
|
1 c |
+ |
1 c |
− |
1 . |
|
|||
1 |
|
|
|
|||||||||
|
|
|
|
6 |
1 |
|
6 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение системы |
(4.46) |
дает |
значения c1 = 2; |
c2 = 6; |
||||||||
c3 = 0. Найденные значения |
c1, c2 , c3 |
подставим в уравнения |
||||||||||
(4.42), (4.44) и (4.45) и окончательно получим частные решения системы (4.26). Они имеют вид
y1 = y2 = y3 =1.
Таким образом, выбранные начальные условия (4.46) дали самый простой вариант частных решений (они оказались не функциями, а константами).
Задача 4.5. Используя условия и схему решения задачи 4.4, рассчитать концентрации реагирующих веществ для уравнений нелинейной системы типа IV (см. табл. 1.4) и получить частные решения при произвольно выбранных начальных условиях.
Решение. В этом случае нелинейная система (1.23) имеет
вид
dy1 |
= y1 (y22 − y32 ), |
|
||
dx |
|
|
||
|
|
|
|
|
dy |
2 |
= y2 (y32 − y12 ), |
(4.47) |
|
|
|
|||
dx |
|
|
||
dy |
|
= y3 (y12 − y22 ). |
|
|
|
3 |
|
||
dx |
|
|
||
Система вполне разрешима (случай аналогичен задаче 4.4). Решение системы (4.47) опять ищем методом интегрируемых комбинаций.
154
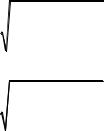
Для составления первой интегрируемой комбинации умножим обе части уравнений системы (4.47) последовательно на y1, y2 и y3 и сложим полученные уравнения. Тогда
y |
dy1 + y |
dy2 + y |
dy3 = 0. |
||
1 |
dx |
2 dx |
3 |
dx |
|
После ее интегрирования имеем |
|
|
|||
|
y2 + y2 + y2 = c . |
(4.47′) |
|||
|
1 |
2 |
3 |
1 |
|
Для составления второй комбинации сначала поделим |
|||||
уравнения системы (4.47) на y1 y2 y3 ≠ 0, |
затем опять после- |
||||
довательно помножим на |
y1, y2 |
и y3 и сложим полученные |
|||
уравнения, получим вторую интегрируемую комбинации вида
1 |
|
y1dy1 |
+ |
|
y2dy2 |
+ |
y3dy3 |
|
= 0. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dx |
|
|
|
dx |
|
dx |
||||||
|
y1 y2 y3 |
|
|
|
|
|
|
|
|
||||||
После интегрирования второй комбинации получим |
|||||||||||||||
|
|
|
|
y1 y2 y3 = c2. |
|
|
(4.47′′) |
||||||||
Объединение (4.47′) и (4.47′′) дает систему |
|||||||||||||||
|
|
|
2 |
|
|
|
2 |
2 |
= c1, |
|
|
||||
|
|
y1 |
+ y2 |
|
+ y3 |
|
(4.48) |
||||||||
|
|
|
|
y |
|
|
|
y = c . |
|
|
|||||
|
|
y |
2 |
|
|
|
|||||||||
|
|
|
1 |
|
|
3 |
2 |
|
|
|
|
||||
Нелинейную систему (4.48) можно решить, например, методом замены переменной. Тогда относительно y22 и y32 получим следующие выражения:
|
2 |
|
(c1 − y12 ) |
|
(c1 − y12 )2 |
|
|
c2 |
|
|||
|
= |
|
|
+ |
|
|
− |
2 |
|
, |
||
y2 |
|
|
|
|
|
|
||||||
|
2 |
|
4 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
y1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(4.48′) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c1 |
− y12 ) |
|
(c1 |
− y12 )2 |
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|||||
y2 |
= |
|
|
− |
|
|
− |
|
2 |
. |
||
|
|
|
|
|
|
|||||||
|
3 |
|
|
2 |
|
|
4 |
|
|
y12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155
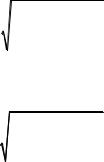
Составив разность квадратов (4.48′), получаем
y2 |
− y2 |
= 2 |
(c1 − y12 )2 |
− |
c2 |
(4.48′′) |
|
|
2 |
. |
|||||
4 |
|
||||||
2 |
3 |
|
|
y2 |
|
||
|
|
|
|
|
1 |
|
|
Затем, подставив в (4.48′′) первое уравнение системы (4.47), получим
dy |
= y 2 |
(c1 |
− y12 )2 |
− |
c2 |
(4.48′′′) |
|
1 |
|
|
2 |
. |
|||
dx |
|
4 |
|
||||
1 |
|
|
y2 |
|
|||
|
|
|
|
|
1 |
|
|
Возведя в квадрат обе части (4.48′′′) и выполнив тождественные преобразования, приходим к уравнению вида
dy1 |
2 |
= y6 |
−2c y4 |
+c2 y2 |
−4c . |
(4.49) |
|
|
dx |
|
1 |
1 1 |
1 1 |
2 |
|
|
|
|
|
|
|
|
|
С учетом замечания к задаче 4.4 для нахождения общего решения (4.49) опять (общий случай) приходится строить систему решений в эллиптических функциях. Построение таких решений (4.49) в эллиптических функциях приведены в п. 4.4.4.
Остановимся пока на некоторых частных случаях найденных решений.
Случай 1. Пусть c2 → 0. Тогда уравнение (4.49) можно записать как
dy1 |
= ±y1 (y12 −c1 ). |
(4.49′) |
dx |
|
|
Уравнение (4.49′) распадается на два простейших дифференциальных уравнения с разделяющимися переменными. Рассмотрим первое из них:
dy1 |
= y1 (y12 −c1 ) . |
(4.49′′) |
dx |
|
|
156

Разделяя переменные в (4.49′′) и интегрируя методом неопределенных коэффициентов, получим
dy1 |
|
dy1 |
* |
|
|
|
= dx, |
∫ |
|
= x +c |
. |
y1 (y12 −c1 ) |
y1 (y1 − c1 )(y1 + c1 ) |
||||
Пусть для определенности c1 > 0. Методом неопределенных коэффициентов находим его неявное решение в виде
y2 |
−c |
= c e |
−2c x |
|
1 |
1 |
1 . |
||
y2 |
||||
3 |
|
|||
|
1 |
|
|
|
Перейдем теперь от неявного вида решения к явному:
y2 |
= |
|
|
|
c1 |
. |
(4.50) |
|
|
|
|
|
|
||||
1 |
|
1 |
−c |
|
e−2c1x |
|
|
|
|
|
|
|
3 |
|
|
|
|
Далее находим y2 |
и y3 |
путем подстановки (4.50) в (4.48′) |
||||||
и с учетом того, что с2 = 0. |
|
|
|
|
|
|||
y2 |
= |
c1 c2 |
, |
y2 |
= 0. |
(4.50′) |
||
c |
−e2c1x |
|||||||
2 |
|
|
3 |
|
|
|||
|
|
3 |
|
|
|
|
|
|
Извлекая квадратные корни из (4.50) и (4.50′), окончательно получим ответ первого случая (при арифметических значениях квадратных корней):
y = |
|
|
|
|
c1 |
|
|
; y |
2 |
= |
|
c1 c2 |
|
; |
y = 0, |
(c |
= 0). |
(4.50′′) |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
1 |
−c e−2c1x |
|
|
|
c |
−e2c1x |
|
3 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Функции |
|
(4.50′′) |
будут |
исследованы |
на |
экстремум |
|||||||||||||||
в п. 4.4.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зададим |
|
теперь начальные |
условия, |
например, |
в |
виде |
|||||||||||||||
y1 (0) = y2 (0) = |
1 |
(задача |
|
Коши). |
Тогда |
получим |
c1 |
= 1 , |
|||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
c2 = 0, c3 = −1.
157
Подставив значения c1, c2 и c3 в (4.50′′), приходим к частным решениям вида
y1 = |
|
|
1 |
|
|
|
|
; |
|
|
y2 = |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
; |
y3 = 0. |
(4.50′′′) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||
|
2 2 1+e− |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
2 2 1+e |
4 |
|
|
|
|
|
|
|
|||||||||||||||
Исследуем сначала предельные случаи для (4.50′′′): |
|
||||||||||||||||||||||||||||||||
lim y = lim y |
|
= 1 ; |
|
|
lim |
y |
= |
|
|
1 |
; |
|
|
lim |
y |
|
= 0. |
|
|||||||||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
x→0 1 |
x→0 |
2 |
4 |
|
|
|
|
x→+∞ 1 |
2 |
|
|
x→+∞ |
|
2 |
|
|
|||||||||||||||||
Если теперь рассмотреть случай c1 < 0, |
|
то получим общие |
|||||||||||||||||||||||||||||||
решения уравнения (4.49′′) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
y1 = |
|
|
c1 |
|
|
|
|
; y2 = |
|
|
|
c1 c2 |
; y3 = 0. |
|
|||||||||||||||||||
1−c |
e2c1x |
|
c −e−2c1x |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При начальных условиях, например y1 ( |
0) = |
1 |
; y2 ( |
0) = 3 , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
частные решения имеют следующий вид: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y = |
|
3 |
|
|
|
|
|
|
; |
y |
|
= |
|
|
36.1 |
|
|
; |
y |
|
= 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
145e−18x −1 |
|
|
|
|
|
|
|
e18x −145 |
3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
при допустимых ограничениях 145e18x −1 ≠ 0 и e18x −145 > 0. |
|||||||||||||||||||||||||||||||||
Случай 2. Пусть |
c1 → 0 (с2 ≠ 0). |
Тогда уравнение |
(4.49) |
||||||||||||||||||||||||||||||
запишется как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dy1 |
2 |
= y6 |
−4c . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Преобразуем его к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dy1 |
|
|
|
= dx |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
−4c |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(здесь опять выбраны арифметические значения корней).
158

Проинтегрируем его:
|
|
∫ |
|
|
|
|
dy1 |
|
= x +с3. |
(4.51) |
||||
|
|
|
|
y6 |
|
|
|
|||||||
|
|
|
|
|
−4c |
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
Если в (4.51) принять |
|
−4с2 =1, то интеграл левой части |
||||||||||||
(4.51) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
dy1 |
|
|
= |
1 |
F(ϕ,k), |
|
(4.51′) |
|||
|
|
y16 +1 |
24 3 |
|
||||||||||
где ϕ(x) = arccos |
(1− |
3)x2 |
+1; |
k = sin 5π = |
2 + 3 |
, а F(ϕ,k) – |
||||||||
( |
|
) |
|
|
|
|||||||||
|
|
|
2 |
|
|
|
12 |
2 |
|
|||||
|
1+ |
3 |
|
|
x |
+1 |
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
функция, зависящая от |
|
ϕ и k |
и являющаяся эллиптическим |
|||||||||||
интегралом 1-го рода (см. формулу (2.60) п. Д. 2.2.6.). Таким образом, случай 2 сразу приводит к построению эллиптических интегралов.
В заключение этого пункта проиллюстрируем на графике поведение кривых y1 и y2 , полученных при начальных усло-
виях y1 (0) = y2 (0) = 14 по формуле (4.50′′′) случая 1. Графики
зависимости концентраций веществ с1 и с2 ( y1 и y2 ) от времени t (x) при с3 = 0 ( y3 = 0) приведены на рис. 4.2.
y
y3 = 0
1,0
0,5
0,36
0,25
y1 y2
|
x |
0 |
Рис. 4.2
159
4.4.1. Исследование некоторых физико-химических параметров реакции сложного типа
Характеристика и общие свойства физико-химических параметров сложной реакции приведены в п. 1.3, там же рассмотрен пример математического описания, для которого выбраны параметры динамической системы с учетом процесса диффузии. В этом пункте приводятся результаты исследований физи- ко-химических параметров на примерах реакций III и V типов табл. 1.4. Для всех типов реакций, приведенных в табл. 1.4, получены аналитические решения системы (1.23) методом интегрируемых комбинаций. Метод подробно рассмотрен на примере реакции второго типа, для которой проведен детальный анализ полученных результатов (см. п. 2.3.2).
Результаты аналитических решений сведены в табл. 4.2.
|
|
|
|
|
Таблица 4.2 |
|
Результаты аналитических решений |
||||
|
|
|
|
||
Типы реакций |
|
Аналитические решения или дифференциальные |
|||
системы |
|
|
уравнения, полученные из системы (1.23′) |
||
(1.23′′) |
|
|
|||
|
|
|
|
|
|
I |
|
y1 = c1 + c2e−x , y2 = c12 +(2c1c2 x + c3 )e−x −c22e−2x , |
|||
|
y3 = c12 + (2c1c2 x −c2 + c3 )e−x −c22e−2x |
||||
|
|
||||
II |
|
y1′2 = |
|
1 |
(c1 + c2 − 2 y12 )(c2 − 2c1 + y12 ) |
|
2 |
||||
|
|
|
|
||
III |
|
y1′2 = |
|
1 |
y1 (4 y13 − 2c1 y12 + c12 y1 − 4c2 ) |
|
4 |
||||
|
|
|
|
||
IV |
|
y1′2 = y12 (y14 − 2c1 y12 + c12 )− 4c2 |
|||
V |
|
y1′2 = y12 (y14 − 2(c1 + 2c22 ) y12 + c12 ) |
|||
160
