книги / Математическое моделирование кинетики сложных химических реакций. Ч. 1

Отсюда следует, что при

схема (3.31) при l = 2 имеет второй порядок аппроксимации. При этом α1 может быть выбрано произвольно. Наиболее широко применяются схемы (3.31) с α1 =1 и α1 =1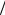2. Заметим также, что путем выбора α1 повысить порядок аппроксимации схемы (3.31) при l = 2 нельзя.

При α1 =1 из (3.38) получим p1 = p2 =1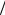2, и схема (3.31)

Геометрическая интерпретация этой формулы представлена на рис. 3.1. Сначала по методу Эйлера находим точку yi+1 = ui + hf (xi ,ui ), затем находим среднее значение угла на-

клона касательной к интегральным кривым на шаге h: tg α = 12 (ui′+ yi′+1 ) и по нему уточняем значение ui+1.

Рис. 3.1

121

Аналогичные выкладки справедливы и для случая α =1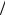2.

Подобные схемы носят название «предиктор – корректор». Выше были рассмотрены схемы со вторым порядком ап-

проксимации. Аналогичные рассуждения могут быть проведены и для схем более высокого порядка (l > 2). При этом при-

ходится налагать на функцию f (x, y) все более высокие тре-

бования гладкости.

Наиболее широкое практическое применение находят схемы четвертого порядка. На компьютерах в виде программ обычно реализуется следующая схема:

Можно проверить, что схема (3.40) имеет четвертый порядок аппроксимации.

В силу теоремы 3.1 для определения порядка сходимости схем Рунге – Кутта достаточно доказать их устойчивость. Это доказательство можно провести в полной аналогии с доказательством устойчивости схемы Эйлера. Действительно, все схемы типа (3.31) имеют вид

122

где функция G(x,y) представляет собой линейную комбинацию функций f(x,y) от промежуточных значений аргумента. Поэтому оценки для функции G(x,y) и ее производных легко выразить через соответствующие оценки функции f(x,y) и ее производных, используемые при доказательстве устойчивости метода Эйлера, откуда и следует сделанное утверждение.

В частности, имеет место следующая теорема.

Теорема 3.2. Пусть функция f(x,y) имеет в D непрерывные частные производные четвертого порядка. Тогда схема Рунге–Кутта (3.40) сходится с четвертым порядком точности, т.е.

uh −[y]h < Ch4.

В заключение отметим, что схемы Рунге–Кутта допускают вычисления с переменным шагом. Начиная с любого индекса i, можно уменьшить или увеличить последующий шаг сетки.

Замечание. В этом подразделе разобраны численные методы решения задачи (3.7) для одного скалярного уравнения первого порядка. Без существенных изменений рассмотренные методы переносятся на случай для нормальной системы уравнений первого порядка [32].

3.3.Численные методы интегрирования дифференциальных уравнений

Рассмотрим далее кратко некоторые из основных методов. Более подробно с ними можно ознакомиться, используя указанную выше литературу.

3.3.1. Метод Эйлера-Коши

Метод представляет собой простейший метод первого порядка численного интегрирования дифференциальных уравнений и реализуется следующей рекуррентной формулой:

123

где h – шаг интегрирования (приращение переменной x). Этот метод обладает большой погрешностью и имеет систематическое накопление ошибок. Погрешность метода R (h2), т.е. пропорциональна h2 (квадрату шага интегрирования).

3.3.2. Метод Эйлера-Коши с итерациями

Метод заключается в вычислении на каждом шаге начального значения по формуле (3.43)

y0 + = y + hf (x , y )

j(i 1) ji j i ji

и уточнении решения с помощью итерационной формулы

Итерации проводятся до тех пор, пока не совпадет заданное число цифр результата на двух последних шагах итераций. Погрешность метода R (h3). Обычно число итераций не должно превышать 3–4, иначе нужно уменьшить шаг h.

3.3.3. Модифицированный метод Эйлера

Метод реализуется следующими рекуррентными формулами:

Данный метод дает погрешность R (h3) и имеет меньшее время вычислений, так как вместо нескольких итераций произ-

водится вычисление только одного значения y* + .

j(i 1/ 2)

124

3.3.4. Метод трапеций

Метод является одной из модификаций метода Эйлера второго порядка и реализуется применением на каждом шаге формулы

где K j1 = hf j (xi , y ji ), K j2 = hf j (xi + h, y ji + K j1 ).

Метод дает погрешность R (h3) и относится к общим методам Рунге-Кутта (см. п. 3.3.5).

3.3.5. Метод Рунге–Кутта четвёртого порядка

Этот метод является наиболее распространенным методом решения систем (3.1) при постоянном шаге (h = const). Достоинства метода − высокая точность (погрешность R (h5)) и по-

При переходе от одной формулы к другой задаются или вычисляются соответствующие значения x и yj и находятся по

подпрограмме значения функции f j (x, y j ).

Решение одного дифференциального уравнения данным методом производится по приведенным формулам (3.47), если

125

в них опустить индекс j, а из алгоритма исключить циклы. Последнее резко упрощает программу и позволяет получить минимально возможное время счета [36].

3.3.6. Метод Рунге–Кутта для дифференциального уравнения второго порядка

Дифференциальное уравнение имеет вид

Метод реализуется с помощью следующих формул [19]:

Перед началом вычислений необходимо задать шаг h и начальные значения x0 , y(x0 ) = y0 и y′(x0 ) = y0′.

3.3.7. Метод Рунге–Кутта с автоматическим изменением шага

Автоматическое изменение шага в ходе решения систем дифференциальных уравнений необходимо, если решение следует получить с заданной точностью. При высокой точности

126

(погрешность ε =10−3 ) и решении в виде кривых с сильно раз-

личающейся крутизной автоматическое изменение шага обеспечивает уменьшение общего числа шагов в несколько раз, резко уменьшает вероятность возникновения числовой неустойчивости, дает более равномерное расположение точек графика кривых (решений) при их выводе на печать.

Метод заключается в том, что после вычисления y j(i+1) с шагом h все вычисления проводятся повторно с шагом h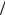2.

в противном случае шаг уменьшается. Если это неравенство слишком сильное, шаг, напротив, увеличивают.

При той же погрешности R (h5) лучшие результаты дает описанный ниже метод.

3.3.8. Метод Рунге–Кутта–Мерсона

Этот метод обеспечивает приближенную оценку погрешности на каждом шаге, которая имеет порядок h5. Метод реализуется следующим алгоритмом:

1. Задается число уравнений N, погрешность ε = E, начальный шаг интегрирования h = H и начальное значение

x0 , y10 , y20 , …, yN 0.

2. С помощью пяти циклов с управляющей переменной j =1, 2, …, N вычисляются коэффициенты:

127

3. Находится (в последнем цикле) значение

Если первое условие не выполняется, шаг h делится на 2 и вычисления повторяются с п.2, после восстановления начальных значений y ji . Если это условие выполняется и выпол-

няется второе условие, значения xi+1 = xi + h и y j(i+1) выводятся

на печать. Если второе условие не выполняется, шаг h увеличивается вдвое и вычисления опять повторяются с п. 2.

Таким образом, y j(n+1) выводится на печать только при

одновременном выполнении условий (3.53) четвёртого пункта. Все описанные выше алгоритмы решения систем ОДУ относятся к одношаговым методам и основаны на вычислениях по рекуррентным формулам, содержащим данные, полученные из решения на одном предшествующем шаге. Эти методы реализуются по явной разностной схеме и обеспечивают автоматическое начало вычислений при заданных начальных условиях и изменение (в том числе автоматическое) шага в ходе вы-

числений.

128

Многошаговые методы решения ОДУ базируются на использовании данных решения на нескольких предыдущих шагах. Это позволяет повысить скорость вычислений. Однако для начала вычислений приходится выполнять несколько первых шагов одношаговыми методами. Аналогично это делается при каждой смене шага интегрирования. Ввиду сложной программной реализации многошаговых, а также неявных методов численного интегрирования они редко используются при решении задач на ПЭВМ. Неявные методы численного интегрирования в основном используются для интегрирования так называемых «жёстких» систем дифференциальных уравнений, описывающих кинетику химических реакций с сильно отличающимися значениями констант скоростей (на порядки). Их достоинством является численная устойчивость решения. Алгоритмы реализации этих методов приведены, например, в ра-

ботах [33, 35, 37, 38].

3.4. Общие выводы по главе 3

Из анализа главы 3 вытекают следующие основные выводы:

–прямая задача химической кинетики сводится к задаче Коши, т.е. к решению системы обыкновенных дифференциальных уравнений 1-го порядка при заданных начальных условиях

вначальной точке;

–основу численных методов решения обыкновенных дифференциальных уравнений составляют теория аппроксимации (в данном случае аппроксимация производных), рекуррентные формулы и итерационные методы;

–универсальным и эффективным численным методом решения обыкновенных дифференциальных уравнений является метод конечных разностей, в котором исходное дифференциальное уравнение (относительно функции непрерывного аргумента) заменятся разностным уравнением (относительно функции дискретного аргумента – сеточной функции). Переход от исходного уравнения к уравнению разностному осуществ-

129

ляется путем аппроксимации производных, входящих в исходное дифференциальное уравнение, соответствующими конеч- но-разностными соотношениями. Решение дифференциального уравнения в итоге сводится к нахождению значений сеточной функции, являющихся приближенными значениями искомой функции в дискретных точках – узлах сетки;

– под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих исходное дифференциальное уравнение (или систему) и начальные условия в начальной точке. Следует отметить, что не всякая разностная схема даёт достаточную точность аппроксимации значений искомой функции в узлах сетки. Важную роль в этом играют устойчивость, аппроксимация и сходимость разностной схемы. Для каждой решаемой задачи существует семейство разностных схем, зависящих от параметра h – шага сетки (расстояние между соседними дискретными точками аргумента). Основным в теории разностных схем является вопрос о сходимости семейства приближенных решений к точному решению исходной дифференциальной задачи при стремлении параметра h к нулю. В случае сходимости при уменьшении шага сетки h < 1 погрешность решения задачи ε(x) в некоторой точке x уменьша-

ется в зависимости от порядка аппроксимации k применяемой разностной схемы: ε(x) = O(hk );

– важнейшим вопросом при применении метода конечных разностей является также устойчивость разностной схемы. Под устойчивостью схемы понимается непрерывная зависимость ее решения от входных данных (коэффициентов уравнений, правых частей, начальных условий), т.е. малому изменению входных данных соответствует малое изменение решения. В противном случае разностная схема является неустойчивой. Если разностная схема устойчива и аппроксимирует исходную дифференциальную задачу, то она сходится, т.е. из устойчивости и аппроксимации разностной схемы следует её сходимость.

130