книги / Математическое моделирование кинетики сложных химических реакций. Ч. 1

где ρi – заданные весовые коэффициенты. В некоторых случа-

ях применяются и другие нормы, например энергетические.

Определение. Будем говорить, что семейство сеточных функций {uh} сходится к точному решению y(x) исходной задачи, если

где через [y]h обозначены значения функции y(x) на сетке ωh.

где C и k – некоторые постоянные, не зависящие от h, то будем говорить, что имеет место сходимость порядка k в соответствующей норме.

3.2.2. Разностная схема Эйлера

Рассмотрим простейшую дифференциальную задачу (3.7) или (3.9). Заменив выражение для производной в точке xn приближенным отношением

поставим в соответствие (3.9) следующую разностную задачу:

В данном случае значения сеточной функции вычисляются по рекуррентной формуле очень просто. Имеем последовательно

111

u0 = y0 ,

u1 = u0 + hf (x0 ,u0 ),

uk = uk−1 + hf (xn−1,un−1 ),

Разностные схемы такого типа называются явными схемами.

Разностная схема (3.15) называется разностной схемой Эйлера с постоянным шагом для задачи (3.9).

Из соответствующих теорем [34] следует, что для непрерывной в области D функции f (x, y), удовлетворяющей усло-

вию Липшица по переменной y, в данном простейшем случае выполняется условие (3.13) в норме (3.11), что позволяет утверждать сходимость сеточных функций, построенных по схеме Эйлера, к решению исходной задачи (3.9). При этом можно также доказать [34], что порядок сходимости при h → 0 последовательности сеточных функций, построенных по разностной схеме Эйлера, составляет k = 1 (сходимость первого порядка).

Сеточная функция uh и решение дифференциального уравнения y удовлетворяют уравнениям разной природы. По-

этому в общем случае не всегда удается повторить выкладки, приводящие для простейшей схемы Эйлера к оценке порядка ее сходимости. В частности, для сеточной функции uh , яв-

ляющейся решением достаточно сложной разностной схемы, трудно предложить такой алгоритм интерполяции, чтобы полученная кривая являлась интегральной кривой дифференциального уравнения, в определенном смысле близкого к исходному, и можно было бы воспользоваться методом дифференциальных неравенств для оценки разности между решением исходного и полученного дифференциальных уравнений. Следует также отметить, что в более сложных случаях разностных схем необходимо убедиться в существовании решения соот-

112

ветствующей разностной задачи, прежде чем выяснять вопрос её сходимости. В общем случае для оценки сходимости приходится использовать другие пути, вводя понятия аппроксимации и устойчивости разностной схемы [34].

3.2.3. Порядок аппроксимации разностной схемы

Для рассмотрения понятия порядка аппроксимации разностной схемы введем норму ϕh – правой части разностной схемы (3.10). Как отмечалось выше, ϕh представляет собой правую часть уравнения – сеточную функцию fh в совокупности с дополнительными условиями для искомой сеточной функции uh.

Пронумеруем их в определенном порядке. Соответствую-

стной схеме (3.10), то, найдя решение разностной схемы uh , получим значение точного решения в узлах сетки [y]h = uh.

Такое положение встречается крайне редко. Как правило, при подстановке значений [y]h в разностную схему (3.10)

тождества не получается, а (3.10) удовлетворяется с некоторой невязкой:

113

Величина невязки δϕh разностной схемы на решении исходной

задачи и является характеристикой аппроксимации разностной схемы исходной задачи.

Функция дискретного аргумента, [y]h , очевидно, является

решением разностной схемы (3.10) с видоизмененной, или, как говорят, возмущенной правой частью ϕh +δϕh.

Теперь перейдем к определению понятия порядка аппроксимации разностной схемы на решении дифференциальной задачи.

Определение. Будем говорить, что разностная схема имеет k-й порядок аппроксимации на решении исходной задачи, если существует такое h0 , что при h ≤ h0

где C и k – некоторые постоянные, не зависящие от h.

Определим порядок аппроксимации схемы Эйлера (3.15), предполагая, что функция f(x, y) в уравнении (3.7) имеет первые непрерывные частные производные по обоим аргументам в прямоугольнике D. В этом случае точное решение y(x) исходной задачи, очевидно, имеет вторую непрерывную производную. Это позволяет записать разложение

В силу (3.19) при подстановке точного решения y(x) задачи (3.7) в левую часть уравнения (3.15) получим

y′(xi ) + h2 y′′(xi +0h) − f (xi , y(xi )) = h2 y′′(xi +θh), (3.20)

(первое и третье слагаемые в левой части (3.20) взаимно уничтожаются, поскольку y(x) является точным решением уравнения (3.7)). Тем самым невязка в уравнении имеет первый поря-

114

док. Решение разностной задачи (3.15) удовлетворяет тому же начальному условию, что и решение задачи (3.9), откуда следует, что схема Эйлера аппроксимирует задачу (3.9) с первым порядком.

Первый порядок аппроксимации схемы Эйлера связан с тем, что в этом методе первая производная y′(xi ) аппроксими-

руется разностным отношением ( yi+1 − yi )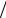h. Выбирая другие

приближенные формулы для первой производной, можно повысить порядок аппроксимации. Например, заменив первую производную симметричным разностным отношением в соседних точках

y′(xi ) ≈ ( yi+1 − yi−1 )(2h),

можно доказать, проводя рассуждения, аналогичные предыдущим, что соответствующее разностное уравнение в этом случае аппроксимирует исходное уравнение (3.7) со вторым порядком.

Естественно предположить, что для того чтобы решение uh разностной схемы было близко к решению исходной задачи, невязка δϕh должна быть достаточно малой. Возникает вопрос, является ли малость невязки δϕh достаточной для того, чтобы обеспечить близость uh к решению исходной задачи,

т.е. обеспечивается ли сходимость разностной схемы, если имеет место аппроксимация? Оказывается, одной аппроксимации, вообще говоря, недостаточно чтобы разностная схема давала приближенное решение дифференциальной задачи. Помимо аппроксимации разностная схема должна удовлетворять некоторым дополнительным свойствам. Таким необходимым свойством является устойчивость разностной схемы.

115

3.2.4. Устойчивость разностной схемы

Рассмотрим разностную схему (3.10) и соответствующую возмущенную задачу

где δϕh называется возмущением входных данных. Рассмот-

рим далее случай, когда возмущенная задача (3.21) однозначно разрешима при достаточно малом возмущении, т.е. существуют такие δ0 и h0 , что при δϕh 1 < δ0 и h < h0 задача (3.21)

где δfh – норма возмущения правой части уравнения, а δuh 0 – норма возмущения дополнительных условий.

Определение. Схема (3.10) называется устойчивой по начальным условиям и правой части уравнения (или просто устойчивой), если существует такая постоянная h0 , что при

h < h0 для нормы погрешности решения выполняется неравенство

где постоянная C не зависит от h.

Данное определение означает непрерывную зависимость решения разностной схемы (3.10) от входных данных задачи – начальных условий и правой части уравнения: малое изменение входных данных приводит к малому изменению решения.

116

Следует отметить, что в случае линейного оператора Lh

введенное определение устойчивости разностной схемы (3.10) эквивалентно требованию, чтобы схема (3.21) была однозначно разрешима при достаточно малом возмущении δϕh и при

h < h0 выполнялось условие

где C – некоторая не зависящая от h постоянная [32].

Можно доказать устойчивость схемы Эйлера (3.15) в случае общей задачи (3.7) при условии, что функция f(x, y) непрерывна в области D и удовлетворяет условию Липшица по переменной y.

3.2.5. Теорема о сходимости

Введенные выше понятия порядка аппроксимации и устойчивости разностной схемы позволяют доказать следующую теорему, играющую фундаментальную роль при исследовании сходимости разностных схем [34].

Теорема 3.1. Если разностная схема (3.10) устойчива и аппроксимирует задачу (3.8) с порядком k, то решения uh при h → 0 сходятся к решению y(x) дифференциальной задачи, причем порядок сходимости также равен k, т.е. имеет место оценка

где постоянная C не зависит от h.

Доказательство. Обозначим разность значений сеточных функций uh и [y]h через zh:

117

Однако значение x* неизвестно. В схеме Эйлера положено x* = xi , что и дает всего лишь первый порядок точности.

Основная идея метода Рунге – Кутта заключается во введении в разностную схему ряда дополнительных параметров, уточ-

няющих приближенное определение значения x*.

Далее рассмотрим начальную задачу (3.7) (или (3.9)):

ваны ниже.

Сопоставим с задачей (3.7) следующую разностную схему:

Kl = f (xi +αl−1h, ui +αl−1hKl−1 ),

а p1,…, pl , α1,…,αl−1 – параметры, выбором которых можно обеспечить требуемый порядок аппроксимации схемы (3.31) на решении задачи (3.30).

Вчастном случае при l = 1, p = 1 схема (3.31) переходит

всхему Эйлера (3.15), имеющую первый порядок аппроксимации. Покажем, что при l = 2 можно так выбрать параметры

p1, p2 и α1, что схема (3.31) будет иметь второй порядок ап-

119

проксимации. Пусть функция f (x, y) имеет в D непрерывные

частные производные до второго порядка по обоим аргументам, что достаточно для существования непрерывной третьей производной от решения. Тогда решение задачи (3.30) может быть представлено по формуле Тейлора

+ hy′′(xi )(1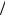2 −α1 p2 ) +O(h2 ).

120