
2939
.pdf
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
m |
|
|
|
|
|
|
|
|
|
(n |
1)a |
0 |
a |
|
x |
i |
|
|
a |
2 |
x |
2 ... |
a |
m |
x m |
|
y |
i |
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
i |
|
i |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
i 0 |
|
|
|
i |
0 |
i |
0 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
n |
|
|
m |
|
|
|
|
|
||
|
a |
0 |
x |
i |
|
a |
|
|
x 2 |
|
a |
2 |
|
x3 |
... a |
m |
|
|
x m 1 |
|
x |
i |
y |
i |
(2.32) |
|||
|
|
|
|
|
1 |
|
|
i |
|
|
|
i |
|
|
|
i |
|
|
|
|||||||||
|
|
|
i 0 |
|
|
|
|
i |
|
0 |
|
|
|
|
i |
0 |
|
|
i 0 |
|
i |
0 |
|
|
|
|
|
|
|
|
|
.......... .......... .......... .......... .......... .......... .......... .......... .... |
|
|
|
|
|
||||||||||||||||||||
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
||
a |
0 |
|
x m |
|
|
a |
|
x m 1 |
|
a |
2 |
|
x m 2 ... |
a |
m |
x 2m |
|
|
|
x m y |
. |
|||||||
|
|
i |
|
|
|
1 |
|
|
i |
|
|
|
|
i |
|
|
|
i |
|
|
|
|
i i |
|
||||
|
i |
|
0 |
|
|
|
i |
0 |
|
|
|
|
|
|
i |
0 |
|
|
|
i |
0 |
|
i 0 |
|
|
|
|
|
Решая эту систему линейных уравнений, получаем коэффици-
енты a0 , a1,..., am .
3. Интегральное приближение функции по способу наименьших квадратов. Рассмотрим теперь случай, когда заданную
на промежутке a;b непрерывную функцию надо аппроксимировать обобщенным многочленом:
|
|
|
|
P(x) |
a0 X 0 (x) |
a1 X1(x) |
... |
an X n (x) |
так, |
||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
чтобы величина интеграла |
|
Y |
[P(x) |
f (x)]2 dx |
(2.33) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
была бы наименьшей. |
|
|
|
|
|
|
|||||||||
|
|
|
Для того чтобы получить минимум интеграла Y , как и в пре- |
||||||||||||
дыдущем |
случае, |
составим |
|
частные |
производные: |
||||||||||
|
Y |
, |
|
Y |
, |
..., |
|
Y |
и |
приравниваем к нулю. |
|
||||
|
|
|
|
|
|
|
|||||||||
|
a0 |
|
a1 |
|
|
an |
|
|
|
|
|
|
|||
Таким образом, получим систему уравнений:
51

1 |
|
|
Y |
|
b |
|
|
|
b |
|
||||
|
|
|
a0 X 0 |
(x) |
a1 X1 (x) ... |
an X n (x) X 0 (x)dx |
f (x) X 0 (x)dx |
0 |
||||||
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
a0 |
|||||||||||
|
|
|
a |
|
|
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
Y |
|
b |
|
|
|
b |
|
|||||
|
|
a0 X 0 |
(x) |
a1 X1 (x) ... |
an X n (x) X1 (x)dx |
f (x) X1 (x)dx |
0 |
|||||||
|
|
|
|
|
|
|
|
|
||||||
2 |
|
a1 |
|
|||||||||||
|
|
a |
|
|
|
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
.......... .......... .......... .......... .......... .......... .......... .......... .......... .......... ......... |
|
|||||||
1 |
|
|
|
Y |
|
b |
|
|
|
b |
|
|||
|
|
|
|
a0 X 0 |
(x) |
a1 X1 (x) ... |
an X n (x) X n (x)dx |
f (x) X n (x)dx |
0. |
|||||
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
am |
|
|||||||||
|
|
|
|
a |
|
|
|
a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Из которой |
находятся величины a0 , a1,..., an , минимизи- |
|||||
рующие интеграл |
(2.33). |
|
|
|
||||||||||
3. МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Способы решения систем линейных уравнений в основном разделяются на две группы: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (таковы, например, правило Крамера, метод Гаусса, метод главных элементов и др.), и 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов (к числу их относятся метод итерации, метод Зейделя, метод релаксации и др.).
3.1. МЕТОД ГАУССА
Наиболее распространенным приемом решения систем линейных уравнений является алгоритм последовательного исключения неизвестных, который называется методом Гаусса.
Пусть дана система линейных уравнений
a11x1 |
a12 x2 |
... a1n xn |
b1 |
|
a21x1 |
a22 x2 |
... a2n xn |
b2 |
(3.1) |
.......... .......... .......... .......... .. |
|
|||
|
|
|||
an1x1 |
an2 x2 |
... ann xn |
bn |
|
52

Рассмотрим общую схему метода Гаусса для систем, имеющих единственное решение.
Предположим, что a11 0 . В противном случае можно поменять местами первое уравнение с уравнением, в котором коэффициент при неизвестном x1 отличен от нуля. Уравнение, с помощью
которого преобразуют остальные уравнения, называют разрешающим уравнением, а коэффициент этого уравнения при неизвестном, исключаемом из остальных уравнений, - разрешающим элементом.
Разделим первое уравнение системы (3.1) на a11 . Оно примет вид
x |
a(1) x |
2 |
a(3) x |
3 |
... a(n) x |
n |
b(1) |
, |
(3.2) |
1 |
12 |
13 |
1n |
1 |
|
|
где |
a |
(1) |
a |
ij |
/ a |
, b(1) |
b / a . |
|
|
ij |
|
11 |
i |
i 11 |
Умножим разрешающее уравнение (3.1) на a21 и вычтем по-
лученное уравнение из второго уравнения системы (3.1). Аналогично преобразуем остальные уравнения. В результате этих операций система запишется так:
|
|
x |
a(1) x |
2 |
a(1) x |
|
... a(1) x |
n |
b(1) |
|
||||||
|
|
1 |
12 |
|
13 3 |
|
1n |
|
1 |
|
|
|||||
|
|
|
a(1) x |
2 |
|
a(1) x |
|
... |
a(1) x |
n |
|
b(1) |
|
|||
|
|
|
22 |
|
23 3 |
|
|
2n |
|
2 |
, |
(3.3) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
.......... .......... .......... .......... ........ |
|
|
|||||||||||
|
|
|
a(1) x |
2 |
a(1) x |
... |
a(1) x |
n |
b |
(1) |
|
|||||
|
|
|
n2 |
|
|
n3 |
3 |
|
nn |
|
|
n |
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2(1j) |
a2 j |
a1(1j) a21, |
|
|
a3(1j) |
|
a3 j |
a1(1j) a31 |
|
|
||||||
anj(1) |
anj |
a1(1j) |
an1, |
|
|
|
b2(1j) |
|
b j |
b1(1) |
a j1 |
|
( j |
2,3,...., n). |
||
Теперь, оставив без изменения первое уравнение системы (3.3) , можно сделать второе уравнение разрешающим и применить описанную процедуру к системе из n 1 уравнений, исключив неиз-
53

вестное x2 из третьего и последующих уравнений. Получим систему вида:
|
x |
|
a(1) x |
2 |
a(1) x |
3 |
... |
a(1) x |
n |
b(1) |
|
|||||||||
|
1 |
|
12 |
|
13 |
|
|
|
|
1n |
|
1 |
|
|||||||
|
|
|
|
|
x2 |
a23(2) x3 |
... a2(2n) xn |
b2(2) |
|
|||||||||||
|
|
|
|
|
|
|
a33(2) x3 |
... a3(2n) xn |
b3(2) , |
|
||||||||||
|
|
|
|
|
|
|
.......... .......... .......... ....... |
|
|
|||||||||||
|
|
|
|
|
|
|
a |
(2) x |
3 |
... |
a |
(2) x |
n |
b(2) |
|
|||||
|
|
|
|
|
|
|
|
n3 |
|
|
|
nn |
|
n |
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2(1j) |
a2(1j) / a22(1) , |
b2(2) |
|
b2(1) / a22(1) , |
|
a3(2j) |
a3(1j) |
|
a2(2j) a32(1) ,....., |
|
||||||||||
anj(2) |
anj(1) anj(2) |
an(12) , b(j1) |
b j |
|
b2(2) |
a (j12) |
|
( j 3,4,...., n). |
|
|||||||||||
|
Продолжая аналогичные вычисления, приведем систему (3.3) |
|||||||||||||||||||
к эквивалентной системе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
a |
(1) x |
2 |
a |
(1) x |
3 |
|
... |
a |
(1) x |
n |
|
b(1) |
|
|||||
|
1 |
12 |
|
13 |
|
|
|
1n |
|
|
1 |
|
|
|||||||
|
|
|
x2 |
a23(2) x3 ... |
a2(2n) xn |
|
b2(2) |
|
||||||||||||
|
|
|
|
|
|
|
x3 ... |
a3(3n) xn |
|
|
b3(3) |
, |
(3.4) |
|||||||
|
|
|
|
|
|
.......... .......... .......... ....... |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
b(n) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
в котором матрица из коэффициентов имеет треугольный вид. Проведенную последовательность преобразований данной
системы называют прямым ходом в методе Гаусса. Обратным ходом называется последовательное исключение неизвестных, начиная с (n 1) - го уравнения и заканчивая первым.
54

|
|
5x1 |
x2 |
2x3 |
8 |
Пример. Решить систему |
x1 |
4x2 |
x3 |
4 |
|
|
|
x1 |
x2 |
4x3 |
4 |
методом |
Гаусса. |
|
|
|
|
Решение. Разделим первое (разрешающее) уравнение на 5 и |
|||||
вычтем |
преобразованное первое уравнение из второго и третьего |
||||
уравнений исходной системы. В результате получим систему, в которой неизвестное x1 исключено из второго и третьего уравнений
|
|
x |
|
|
1 |
|
x |
|
|
|
2 |
x |
|
8 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
5 |
|
|
2 |
5 |
|
|
3 |
5 |
|
|
|
|
|
|
|
||||||||
|
|
|
21 |
x2 |
7 |
x3 |
|
28 |
||||||||||||||||||
|
|
|
5 |
|
5 |
|
5 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
6 |
|
|
x2 |
|
18 |
x3 |
|
12 |
. |
|||||||||||||
|
|
|
5 |
|
|
5 |
5 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Теперь второе уравнение будет разрешающим с разрешающим |
||||||||||||||||||||||||||
элементом |
21 |
. Разделим второе уравнение на |
|
21 |
|
и вычтем преоб- |
||||||||||||||||||||
5 |
|
5 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
разованное второе уравнение, умноженное на |
|
6 |
|
|
|
из третьего урав- |
||||||||||||||||||||
5 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
нения, исключая тем самым неизвестное x2 в последнем уравнении. Получим систему
|
x |
|
1 |
x |
|
|
|
|
2 |
x |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
5 |
|
2 |
|
|
5 |
|
3 |
|
5 |
|
||
|
|
x2 |
|
1 |
x3 |
|
4 |
|
|
|||||
|
|
3 |
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x3 |
1. |
|
|
|||
|
Далее, подставляя значение x3 |
во второе уравнение, находим |
||||||||||||
x2 |
1. Полученные значения |
x2 |
|
и |
x3 |
подставляем в первое |
||||||||
уравнение и находим x1 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55

Для уменьшения погрешности вычислений существуют различные модификации метода Гаусса. Одна из модификаций метода Гаусса с выбором максимального элемента по столбцу состоит в следующем.
В начале первого шага прямого хода среди коэффициентов ai1 (i 1,2,..., n) при неизвестном x1 находят наибольший по мо-
дулю. Предположим, что это a j1 . После этого в исходной системе
(3.1) можно произвести перестановку: первое уравнение можно поставить на место j - го, а j -е на место первого. Далее вычисления в
описанной ранее последовательности.
В начале второго шага прямого хода максимальный по модулю элемент выбирают среди коэффициентов ai2 (i 1,2,..., n) при неизвестном x2 , снова возможна соответствующая перестановка и исключение неизвестного x2 , начиная с третьего уравнения
т.д., вплоть до последнего шага прямого хода в методе Гаусса. Следует заметить, что процедура прямого хода в методе Гаус-
са может привести не к треугольной матрице (3.4), а к двум другим случаям:
1)число преобразованных уравнений системы меньше числа неизвестных (это происходит, если в процессе преобразований получаются тождества 0=0) – тогда система имеет бесконечное множество решений;
2)все коэффициенты при неизвестных в каком либо уравнении равны нулю, в то время как свободный член уравнения отличен от нуля – тогда система не имеет решения.
3.2.МЕТОД ИТЕРАЦИИ
При большом числе неизвестных линейной системы реализация метода Гаусса, дающего точное решение, приводит к сложным вычислениям. В таких случаях для нахождения корней системы иногда удобнее пользоваться приближенными методами. Рассмотрим один из этих методов – метод итераций.
Пусть дана система линейных уравнений (3.1). Введя в рассмотрение матрицы
56

|
|
|
a11 |
a12 ... |
a1n |
|
|
x |
|
|
|
|
|
b |
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
a21 |
a22 ... a2n |
|
|
x |
2 |
|
|
|
|
b |
|
|||
|
|
A |
|
|
|
|
|
, |
X |
|
, |
|
|
B |
2 |
. |
|
|
|
|
|
|
|
|
... |
|
|
... |
|||||||
|
|
.......... .......... .. |
|
|
|
|
|
|
|
||||||||
|
|
|
an1 |
an2 ... ann |
|
|
xn |
|
|
|
|
bn |
|
||||
систему (3.1) |
можно записать в виде матричного уравнения |
|
|||||||||||||||
|
|
|
|
|
|
|
A X |
b , |
|
|
|
|
|
|
|
(3.5) |
|
|
Предполагая, |
|
|
|
что |
|
диагональные |
коэффициенты |
|||||||||
aii |
0 |
(i |
1,2,...n) , |
|
разрешим первое уравнение системы (3.1) |
||||||||||||
относительно |
x1 , |
второе – относительно x2 и т.д. Тогда получим |
|||||||||||||||
эквивалентную систему |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x1 |
12 x2 |
|
13 x3 |
|
... |
1n xn |
|
|
1 |
|
|
|
|||
|
|
x2 |
21x1 |
|
23 x3 |
|
... |
2n xn |
|
2 |
|
|
(3.6) |
||||
|
|
.......... .......... .......... .......... .. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
xn |
n1x1 |
|
n2 x2 |
|
... |
n,n 1xn |
1 |
|
n , |
|
|||||
|
|
|
|
|
b |
|
|
|
|
|
|
aij |
|
|
|
|
|
где |
|
|
i |
|
i |
, |
|
|
|
ij |
|
|
|
|
при i |
j |
|
|
|
|
aii |
|
|
|
|
aii |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
ij |
0 |
при |
i |
j |
(i, j 1,2,..., n). |
|
|
|
|
|
||||||
Введя матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
11 |
12 ... |
1n |
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
22 ... |
2n |
, |
|
|
|
|
2 |
, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
.......... .......... .. |
|
|
|
|
... |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n1 |
n2 ... |
nn |
|
|
|
|
|
n |
|
|
||
систему |
(3.6) можем записать в матричной форме |
|
|
|
|||||||||||||
57

X |
X . |
(3.7) |
Для решения системы (3.6) применим метод последовательных приближений. За начальное приближение принимаем, напри-
мер, столбец свободных членов x(0)  .
.
Далее, последовательно строим матрицы-столбцы
x(1)  x(0)
x(0) 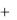 , x(2)
, x(2) 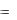 x(1)
x(1)  ,…. , x(k)
,…. , x(k)  x(k 1)
x(k 1)  , …
, …
Если последовательность приближений x(0) , x(1) ,..., x(k) , ...
имеет предел
|
1 |
|
|
lim X (k ) |
|
2 |
, |
|
|||
|
... |
|
|
n
то этот предел является решением системы (3.6) и, следовательно, решением равносильной системы (3.1)
Метод последовательных приближений хорошо сходится, если элементы матрицы  малы по абсолютной величине, для этого модули диагональных коэффициентов системы (3.1) должны быть велики по сравнению с остальными элементами этой матрицы. Для того чтобы процесс итераций сходился к единственному решению этой системы, независимо от выбора начального приближения, необходимо выполнение для приведенной системы (3.6) по меньшей мере одного из условий (достаточное условие сходимости метода итераций)
малы по абсолютной величине, для этого модули диагональных коэффициентов системы (3.1) должны быть велики по сравнению с остальными элементами этой матрицы. Для того чтобы процесс итераций сходился к единственному решению этой системы, независимо от выбора начального приближения, необходимо выполнение для приведенной системы (3.6) по меньшей мере одного из условий (достаточное условие сходимости метода итераций)
n
ij |
1, |
i 1, 2, ..., n |
(3.8) |
|
|
|
|
|
|
|
|
j 1
или
n
ij |
1, |
j 1, 2, ..., n . |
(3.9) |
|
|
|
i 1
58

|
4x1 0.24x2 |
0.08x3 |
8 |
|
Пример. Решить систему |
0.09x1 |
3x2 |
0.15x3 |
9 ме- |
|
0.04x1 |
0.08x2 4x3 |
20 |
|
тодом итерации. |
|
|
|
|
Решение. Приведем эту систему к виду (3.6) |
|
|
||
|
x1 |
2 |
0.06x2 |
|
0.02x3 |
|
|
|
|
|||
|
x2 |
3 |
0.03x1 |
|
0.05x3 |
|
|
|
|
|||
|
x3 |
5 |
0.01x1 |
|
0.02x2 . |
|
|
|
|
|||
Выберем начальное приближение |
x |
(0) |
2, x(0) 3, x |
(0) |
5. |
|||||||
|
|
|
|
|
|
|
1 |
2 |
3 |
|
||
Далее, находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
(1) |
2 |
0.06 |
3 |
0.02 |
5 |
1.92 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2(1) |
3 |
0.03 |
2 |
0.05 |
5 |
3.19 |
|
|
|
||
|
x3(1) |
5 |
0.01 2 |
0.02 |
3 |
5.04. |
|
|
|
|||
Найдем вторые приближения корней |
|
|
|
|
|
|
||||||
|
x |
(2) |
2 |
0.06 |
3.19 |
0.02 |
5.04 |
1.9094 |
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2(2) |
3 |
0.03 1.92 |
0.05 |
5.04 |
3.1944 |
|
|
||||
|
x3(2) |
5 |
0.01 1.92 |
0.02 |
3.19 |
5.0446. |
|
|||||
После новой подстановки будем иметь третьи приближения |
||||||||||||
корней |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
(3) |
1.9092 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2(3) |
3.1949 |
|
и т. д. |
|
|
|
|
|
|||
|
x3(3) |
5.0448 |
|
|
|
|
|
|
|
|
||
С |
точностью |
|
|
0.001 |
|
можно |
принять |
|||||
x1 1.909, |
x2 |
3.1949, x3 |
5.0448. |
|
|
|
|
|
||||
Сходящийся метод итераций обладает важным свойством самоисправляемости, то есть отдельная ошибка в вычислениях не
59

отразится на окончательном результате, так как каждое промежуточное значение неизвестных можно принять за новое начальное приближение. Если процесс итераций сходится, то окончательный результат не зависит от выбора начального приближения.
Условия (3.8), (3.9) сходимости метода итераций накладывают жесткие ограничения на коэффициенты системы (3.6). Однако, если определитель матрицы А не равен нулю, то систему (3.1) с помощью элементарных преобразований всегда можно заменить эквивалентной системой (3.6), для которой условия сходимости будут выполняться. Практически поступают следующим образом. Из заданной системы выделяют уравнения с коэффициентами, модули которых больше суммы модулей остальных коэффициентов уравнения. Каждое выделенное уравне-
ние выписывают в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным. Из оставшихся неиспользованных и выделенных уравнений системы с помощью операций сложения уравнений и умножения уравнений на число получают новые уравнения системы такие, чтобы один из коэффициентов по абсолютной величине оказался больше суммы абсолютных величин остальных коэффициентов. При этом нужно позаботиться, чтобы каждое уравнение исходной системы участвовало в формировании новой системы.
Пример. |
Рассмотрим систему |
|
|
|||
|
2x1 |
3x2 |
4x3 |
x4 |
3 |
(1) |
|
x1 |
2x2 |
5x3 |
x4 |
2 |
(2) |
|
5x1 |
3x2 |
x3 |
4x4 |
1 |
(3) |
|
10 x1 |
2x2 |
x3 |
2x4 |
4. |
(4) |
Решение. |
В уравнении (2) коэффициент при x3 по модулю |
|||||
больше суммы модулей остальных коэффициентов, поэтому можно принять это уравнение за третье уравнение новой системы. Аналогично, уравнение (4) можно взять в качестве первого уравнения новой системы. Для получения уравнения (2) с максимальным по
модулю коэффициентом при x2 достаточно составить разность уравнений (1) и (3). Получим уравнение x1 5x2 x3 1 . Под-
бором убеждаемся, |
что за уравнение (4) можно взять |
линейную |
комбинацию 2 (1) |
(2) 2(3) (4) , т.е. 3x1 9x4 |
10 0 . В |
60
