4. Изгиб

4.1. Статически определимые системы

4.1.1. Построение эпюр поперечных сил и изгибающих моментов для балок

4.1. Для заданной двухопорной балки (рис. 4.1) построить эпюры . Определить наибольшие по абсолютной величине значения . Принять a = 1 м, q = 10 кН/м, P = 1,5qa, m = 2,25qa², a₁ = 3a, a₂ = 1,5a.

Примечание: решение задачи приведено в [2].

4.2. Для заданной консольной балки (рис. 4.2) построить эпюры . Определить наибольшие по абсолютной величине значения . Принять a = 1 м, q = 10 кН/м, P = qa, m = qa², a₁ = 2a, a₂ = a.

Примечание: решение задачи приведено в [2].

Рис. 4.1

Рис. 4.2

4.3. Для балки на двух опорах (рис. 4.3) построить эпюры . Определить наибольшие по абсолютной величине значения .

Решение

1. Определение реакции опор:

;

;

; .

Проверка

2. Разбивают балку на участки, на каждом из них выбирают произвольное сечение, для которого нужно составить аналитические выражения (рис. 4.3,а).

3. Составляют аналитические выражения и вычисляют характерные ординаты эпюр .

Рис.4.3

Ι участок: ; ;

.

Так как меняет знак, то имеет экстремум.

; ;

; ;

; .

ΙΙ участок: ; ;

;

; .

ΙΙΙ участок: ; ;

; ; .

4. По характерным ординатам строят эпюры (см. рис. 4.3,б) и (см. рис. 4.3,в), учитывая, что начало первого и второго участков слева, а третьего – справа.

5. Пользуясь следствиями из дифференциальных зависимостей, проверяют правильность построенных эпюр.

6. По эпюре (см. рис. 4.3,б) определяют , а по эпюре (см. рис. 4.3,в) определяют .

4.4. Построить эпюры для балок, схемы нагружения которых указаны на рис. 4.4, 4.5, рис. 4.6,а-г. Определить наибольшие по абсолютной величине значения .

1 )

2) ,

1)

2)

Рис. 4.4 (начало)

Рис. 4.4 (окончание)

Рис. 4.5 (начало)

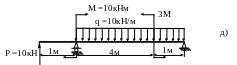
Рис. 4.5 (продолжение)

Рис. 4.5(окончание)

4.5. Определить оптимальную длину консолей “a” балок, схемы нагружения которых представлены на рис. 4.6, д,е, и построить эпюры .

Указание: оптимальной длиной консоли балки называется такая ее длина, при которой максимальный изгибающий момент имеет наименьшее значение. Оптимальная длина консоли определяется из условия равенства абсолютных значений изгибающего момента в сечении над опорой и максимального изгибающего момента внутри пролета между опорами.

4.6. Груз P при помощи вспомогательных балочек, соединенных шарниром S передается на балку ADB в точках A, C, B (см. рис. 4.6, ж). Построить эпюры для вспомогательных балочек и основной балки.

Рис. 4.6 (начало)

Рис. 4.6(окончание)

4.7. Построить эпюры изгибающих моментов, не определяя реакции опор, для балок, схемы нагружения которых указаны на рис. 4.6, з и рис. 4.7,а,б,в.

4.8. Построить эпюры поперечных сил и определить нагрузки, действующие на балки, для которых представлены схемы закрепления и эпюры изгибающих моментов (см. рис. 4.7, г, д, е).

4.9. По эпюрам , указанным (см. рис. 4.7, ж, з) изобразить схемы закрепления и нагружения балок, определить величины нагрузок и построить эпюры . Внешние сосредоточенные моменты к балкам не приложены.

Рис. 4.7 (начало)

Рис. 4.7(окончание)

4.1.2. Расчеты балок на прочность .

4.10. Для балки (см. рис. 4.1) из условия прочности подобрать диаметр d сплошного круглого сечения, размеры b и h прямоугольного сечения с отношением и сечение в виде двух одинаковых, не связанных между собой швеллеров, поставленных вплотную друг к другу ( ][ ). Установить, какое сечение рациональнее, сравнив коэффициенты экономичности . Материал балки – сталь Ст. 3, предел текучести , а коэффициент запаса прочности .

Примечание: решение задачи приведено в [2].

4.11. Для консольной балки (см. рис. 4.2.) из условия прочности подобрать сечение в виде прокатного двутавра и сечение в виде двух одинаковых, не связанных между собой двутавров, поставленных вплотную друг к другу ( ). Установить, какое сечение рациональнее, сравнив коэффициенты экономичности . Материал балки – сталь Ст. 3, предел текучести , а коэффициент запаса прочности .

Примечание: решение задачи приведено в [2].

4.12. Для балки, схема нагружения которой указана (см. рис. 4.3), провести расчет на прочность по нормальным напряжениям для двух видов поперечного сечения:

1. прямоугольника ;

2. двутавра №14. Принять , , .

Решение

Условие прочности для балки постоянного по длине поперечного сечения имеет вид:

.

Расчет проверочный. Из решения задачи 4.3 имеем .

1) Прямоугольное сечение: , .

Условие прочности выполнено.

Для двутавра №14: W_х=81,7 см³.

.

Условие прочности выполнено.

4.13. Балка постоянного поперечного сечения нагружена, как показано (см. рис. 4.3). Определить допускаемое значение интенсивности нагрузки , если , , поперечное сечение состоит из двух швеллеров №20 ( [ ] ).

Решение

Условие прочности для балки постоянного поперечного сечения имеет вид:

,

где - изгибающий момент в опасном сечении.

Вид расчета – расчет допускаемой нагрузки:

.

Для заданного сечения .

Из решения задачи 4.3 имеем ;

; ; .

4.14. Определить величину наибольших касательных напряжений, возникающих в балке, нагруженной, как указано (см. рис. 4.3), если поперечное сечение прямоугольное . Принять , .

Решение

Касательные напряжения определяются по формуле Журавского:

.

Наибольшие касательные напряжения возникают в сечении с в точках нейтральной линии сечения. Из решения задачи 4.3. следует . Для прямоугольного сечения , , для точек нейтральной линии .

Подставив в формулу Журавского, получим:

.

4.15. Определить наибольшие значения нагрузок, которые можно приложить безопасно к балкам, схемы нагружения которых указаны (см. рис. 4.4, в, г, рис. 4.5, е, рис. 4.6, ж). Допускаемое значение напряжения, размеры и форма поперечных сечений указаны на рисунках. Принять .

4.16. Для балок, схематически изображенных (см. рис. 4.4, е, рис. 4.5, б, г), подобрать сечения по наибольшему изгибающему моменту. Формы сечений и допускаемые значения напряжений указаны на рисунках.

4.17. Проверить прочность балок, схемы нагружения которых указаны (см. рис. 4.5, а , в). Формы, размеры сечений и допускаемые значения напряжений указаны на рисунке.

4.18. При непосредственном нагружении балки АВ (рис.4.8) силой Р посредине пролета наибольшие нормальные напряжения превышают допустимые на 30 %. Для устранения перенапряжения поставлена вспомогательная балка СД. Определить необходимую длину “а” этой балки.

4.19. Консоль (рис. 4.9) проектируется как балка равного сопротивления изгибу. Поперечное сечение консоли – прямоугольник высотой h. Установить закон изменения ширины b = b(z) сечения. Максимальное нормальное напряжение в каждом сечении консоли должно равняться [σ]. Решить задачу при нагружении консоли только сосредоточенной силой Р на конце балки постоянной ширины b. Определить .

4.20. Нормальные напряжения, возникающие под действием силы Р в точке С балки треугольного сечения , изображенной на рис. 4.10, равны . Определить величину наибольших по абсолютному значению нормальных напряжений в опасном сечении балки.

4.21. Двое рабочих должны нести стальной брус длиной 2 м с квадратным поперечным сечением см². Если они возьмут его за концы, то чему будет равно наибольшее нормальное напряжение? Если каждый рабочий возьмет брус на одинаковом расстоянии “a” от конца, то в каких местах они должны его взять, чтобы нормальное напряжение не превышало 140 МПа.

Рис.4.11

4. 22. Определить шаг l шпонок в составной консоли (рис. 4.11). Размеры шпонки: мм. Допускаемые напряжения на смятие шпонки , на скалывание шпонки и бруса . Указание: при длине шага l сила сдвига равна ql, где q – сила сдвига на единицу длины.

4.23^*. Определить из условия прочности размер “а” поперечного сечения балки, изображенный на рис. 4.12, если , , , . Выяснить, как рациональнее расположить балку, полкой вверх или вниз?

Р ис. 4.12

Рекомендации

Вследствие того, что материал по разному сопротивляется растяжению и сжатию, наиболее напряженным в данном случае (полкой вверх) оказывается среднее сечение между опорами, хотя в сечении над опорой В изгибающий момент больше.

Ответ: ; рациональное расположение балки – полкой вверх.

4.24^*. Консольная балка АВ нагружена парой сил, приложенных к ее свободному концу (рис. 4.13). Определить оптимальную из условия прочности ширину полки b, если предел текучести материала балки при сжатии в 1,5 раза больше предела текучести при растяжении.

Рис. 4.13

Рекомендации

Условием оптимальности является равенство отношений абсолютных значений наибольшего растягивающего и сжимающего напряжений и пределов текучести при растяжении и сжатии.

Ответ: b = 2,45 a.

4.1.3. Определение перемещений при изгибе балок

4.25. Для балки (рис. 4.14) постоянной жесткости определить прогиб сечения , угол поворота сечения .

Принять , , , поперечное сечение двутавр № 20, для которого .

Решение

Обозначим , .

Определим прогиб с помощью интеграла Мора.

1. Рассмотрим грузовое состояние “Р” – балку, нагруженную заданной нагрузкой (см. рис. 4.14, а). Так как балка шарнирно оперта, определим реакции ; .

Рис. 4.14

2. Рассмотрим фиктивное состояние ( i = “1”) , то есть балку, разгруженную от заданной нагрузки и нагруженную только единичной силой в сечении, прогиб которого определяется (см. рис. 4.14, б).

Определим реакции фиктивного состояния.

; ,

; .

Проверка: .

3.Состояния вычерчиваются одно под другим и одновременно оба разбиваются по участкам грузового и фиктивного состояний; k = 1, 2, 3. Выражения представлены в табл. 4.1.

Таблица 4.1

5. Определяем перемещение по формуле

			0

.

Ответ имеет положительный знак. Это означает, что прогиб направлен вниз (как единичная сила).

Для определения можно использовать способ Верещагина, так как балка имеет только прямолинейные участки постоянной жесткости.

1. Рассмотрим грузовое состояние “P” (рис. 4,15, а).

2. Рассмотрим фиктивное состояние ( “i” = 2), то есть балку, разгруженную от заданной нагрузки и нагруженную только единичным моментом в сечении, угол поворота которого нужно определить (см. рис. 4.15, б).

3. Вычерчиваем указанные состояния одно под другим и строим эпюры изгибающих моментов грузового состояния (см. рис. 4,15, в) и фиктивного (см. рис. 4.15, г).

4. Разбиваем обе эпюры (одновременно по грузовому и фиктивному состояниям) на участки.

5. На каждом из участков эпюры грузового состояния проводим расслоение площади на простейшие.

6. Определяется величина простейшей площади с учетом знака, где k – номер участка, p – указывает, что эпюра грузовая, j – номер площади, и абсцисса центра тяжести простейшей площади (указана звездочкой *).

7. Под центром тяжести площади грузового состояния определяется ордината эпюры фиктивного состояния, где k – номер участка, 2 – указывает номер фиктивного состояния, j – номер площади эпюры грузового состояния.

8. Искомый угол поворота определяем по формуле

= 0,0006 рад > 0.

Ответ имеет положительный знак. Это означает, что поворот сечения происходит против часовой стрелки, т.е. так же, как направлен единичный момент.

Рис. 4.15

Указанный способ расслоения наиболее универсален, так как может быть использован при определении перемещений в балках различной жесткости по участкам. Если жесткость постоянна по длине балки, то можно использовать способ расслоения, изложенный в [2].

4.26. Определить угол поворота на левой опоре, прогибы свободных концов и посередине пролета балок, схемы нагружения которых указаны ранее (см. рис. 4.5, д и рис. 4.7, а, б, в).

4. 27. Определить угол поворота в сечении балки, где приложена сосредоточенная сила Р (см. рис. 4.5, а).

Принять .

4. 28. Определить прогиб посередине пролета балки (см. рис. 4.6,а).

4.29. Определить прогиб и угол поворота на конце консоли (см. рис. 4.4, ж, з). Принять .

4.30. Балка пролетом l = 1м, свободно лежащая на двух шарнирных опорах, изогнута по дуге окружности. Сечение балки прямоугольное со сторонами b = 6см, h = 4см. Прогиб, измеренный посередине пролета, оказался равным 6,25 мм.

Определить величину модуля упругости материала и радиус кривизны оси балки, если .

4.31. Написать выражения для прогиба и угла поворота на конце консоли (рис. 4.16) с учетом того, что заделка поворачивается на малый угол .

4.32. Элемент машины представляет собой балку пролетом 2а, опирающуюся одним концом на шарнирно-подвижную опору, а другим – на вертикальные направляющие, вдоль которых свободно (без трения) скользит ползун, жестко связанный с балкой (см. рис. 4.6, г). Определить величину прогибов т. т. А и С и угол поворота на опоре В в двух случаях:

а) если к балке приложена сосредоточенная сила P в середине пролета;

б) если та же сила будет приложена к ползуну.

4.33. Деревянный брус квадратного сечения см оперт левым концом на подвижную опору А, правый конец В бруса подвешен на стальном стержне сечением F = 2,5 см² (рис. 4.16,а).

Определить прогиб в середине пролета и в сечении В. , .

4.34^*. При каком соотношении моментов инерции и сечений участков АВ и ВС стальной балки (рис. 4.17) прогиб сечения В окажется максимальным?

Рис. 4.16,а Рис. 4.17

4.35. Стальная двутавровая балка № 16 длиной 2 м защемлена одним концом и нагружена равномерно распределенной нагрузкой интенсивности q. Какова может быть наибольшая величина q, если наибольший прогиб не превосходит 2 см²?

4.36. Балка, лежащая на двух опорах, составлена из двух швеллеров № 5 (рис. 4.18). К концам балки жестко прикреплены стойки высотой h = 1м. Определить сближение концов m и n стоек, вызванное равномерно распределенной по балке нагрузкой интенсивностью . Принять , .

4.37^*. Биметаллический элемент (две жестко соединенные металлические пластинки с различными коэффициентами температурного расширения и ) нагревается на некоторую величину Δt. При нагреве биметаллическая пластина изгибается. Установить, как меняется кривизна пластины в зависимости от ее геометрических размеров и температуры нагрева (рис. 4.19).

Рис. 4.19

Рекомендации.

Согласно гипотезе плоских сечений деформация слоя пластины, находящегося на расстоянии y от границы слоев, определяется в виде

,

где - деформация границы слоев; и - радиусы границы слоев пластины до и после ее нагрева (рис. 4.20). Если до нагрева пластина была плоской, то .

С другой стороны , деформации слоев пластины выражаются в виде

; .

Продольная сила и изгибающий момент в каждый момент времени равны нулю.

h₁

h₂

ρ

Рис. 4.20

4.38^*. Найти прогиб в точке А бруса (рис.4.21).

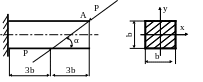
Рис. 4.21

Рекомендации.

При решении такого рода задач важным является умение преобразовать заданную схему в ряд простейших согласно принципу независимости действия сил. В рассматриваемом случае приведенную схему можно представить в виде, представленном на рис. 4.22.

З десь ; ,

где .

Горизонтальная составляющая силы Р вызовет деформацию сжатия только на правой части балки и не будет сказываться на величине искомого прогиба.

Используя способ Мора или Верещагина, определяют искомый прогиб.

Ответ: .

4 .39^*. По заданной форме изогнутой оси балки (рис. 4.23) определить характер и величину нагрузки. На всех участках балки ее ось деформируется по дуге окружности радиуса . Жесткость балки - постоянная.

Рекомендации.

В решении задачи следует использовать известное приближенное уравнение кривизны изогнутой оси балки

и учитывать при этом свойство окружности – постоянство ее кривизны.

Ответ: в точках по оси балки, где прогиб равен нулю, должны быть приложены сосредоточенные моменты, обеспечивающие постоянство изгибающего момента на всех участках балки, вследствие которого согласно уравнению кривизны и .

4.40^*. В какой из балок, изображенных на рис. 4.24 при одинаковом перемещении свободного конца максимальное нормальное напряжение больше?

Р ис. 4.24

Рекомендации.

Чтобы в обоих случаях балки получили одинаковое перемещение свободного конца, необходимо выполнить условие .

Ответ: максимальное нормальное напряжение больше в балке, изображенной на рис. 4.24, б.

4.41^*. Из эксперимента получена форма упругой линии сильно изогнутого гибкого стержня и определена величина силы Р (рис.4.25). Как наиболее просто найти реакции опор?

Рекомендации.

Равнодействующая силы Р и реакции правой опоры проходит через точку перегиба упругой линии стержня (рис.4.26). Из этого условия определяется реакция R.

Остальные реакции определяются из уравнений равновесия: А=Р,В=R,M=Ra.

4.42^*. Консольная балка прямоугольного поперечного сечения (рис.4.27) неравномерно нагрета по высоте (закон изменения температуры задан). Определить вертикальное перемещение δ_Α свободного конца балки. Коэффициент линейного расширения материала балки α, модуль упругости Е.

Рекомендации

Для определения вертикального перемещения свободного конца балки удобно воспользоваться интегралом Мора в виде , где М_Х1 – изгибающий момент от единичной силы; dθ – взаимный угол поворота близлежащих сечений от заданного воздействия.

Ответ:

4.43^*. Ломаная балка, защемленная одним концом, нагружена на другом силой Р.

Подобрать угол наклона линии действия силы α так, чтобы перемещение точки А происходило только по направлению силы Р (рис. 4.28).

Рекомендации

При поставленном условии перемещение точки А в направлении, перпендикулярном к линии действия силы равно

нулю. Из этого условия и определяется угол , где n – любое целое число.

4.1.4. Расчет плоских рам и кривых брусьев малой кривизны

4.44. Для рамы (рис.4.29) построить эпюры внутренних силовых факторов. Вычислить все характерные ординаты этих эпюр. Принять а=1м, q=10кН/м, Р=qa, m=qa², a₁=0,5a, a₂=a, a₃=0,5a. Из условия прочности подобрать размеры коробчатого сечения h,b,t, приняв h/b=2, t=0,2b. Материал рамы сталь Ст3, предел текучести σ_тр=σ_тс=225МПа, а коэффициент запаса прочности n=1,5.

Примечание: решение задачи приведено в [2].

4.45. Для кривого бруса (рис.4.30) построить эпюры внутренних силовых факторов. Вычислить все характерные ординаты этих эпюр. Принять R=1м, P=10kH, m=PR, φ=30⁰.

Из условия прочности подобрать размеры трубчатого сечения D и d. Принять α=d/D=0,6, материал сталь Ст 3, предел текучести σ_тр= σ_тс=225МПа, а коэффициент запаса прочности n=1,5.

Примечание: решение задачи приведено в [2].

4.46. Для рам (рис.4.31,а,б) одинакового сечения на всех участках подобрать размеры сечения из расчета на прочность. Формы сечений и допускаемые напряжения указаны на чертеже.

4.47. Для рамы (рис.4.31,в) определить угол поворота и полное перемещение сечения А. Жесткость всех участков постоянна и указана на рисунке.

4.48. Определить с помощью теоремы Кастилиано прогиб сечения А рамы (рис.4.31,г). Жесткость всех участков постоянна и указана на рисунке.

4.49. Для рамы одинакового сечения на всех участках

(рис. 4.32,а) выполнить проверочный расчет на прочность. Размеры, форма сечения и допускаемое напряжение указаны на рисунке.

4.50. Для кривого бруса (см. рис. 4.32, б) из условия прочности подобрать круглое сечение, приняв [σ] = 160 МПа. Определить горизонтальное и вертикальное перемещения и угол поворота свободного конца. Е = 2·10⁵ МПа.

4.51. Для кривого бруса (см.рис.4.32,в) определить полное перемещение точки приложения силы и угол поворота на правой опоре.

4.52. Для рамы (см.рис.4.32,г) определить интенсивность распределенной нагрузки q из условия прочности. Вид сечения и допускаемое напряжение указаны на рисунке. Определить сближение свободных концов. Е = 2·10⁵ МПа, а=1м.

4.53. Для кривого бруса (см.рис.4.32,д) определить допускаемую величину Р. Размеры, форма сечения и допускаемое напряжение указаны на рисунке.

Рис. 4.31

в)

4.2.Статически неопределимые системы

4.2.1. Статически неопределимые балки

4.54. Для балки постоянной жесткости (рис.4.33) необходимо:

1. Раскрыть статическую неопределимость.

2. Построить эпюры Q_y,M_x.

3. Подобрать из расчета на прочность сечение в форме двутавра.

Принять а=1м, q=10кН/м , [σ]=160МПа.

Решение

1. Раскрытие статической неопределимости. Используем метод сил.

1. Система два раза статически неопределима (4 реакции, 2 уравнения равновесия);

2. Выбирая в качестве «лишних» неизвестных реакции любых двух связей (внутренних или внешних), статически неопределимой балке можно поставить в соответствие различные основные системы (рис.4.34). Выбираем основную систему для решения - (рис.4.34,а), а для проверки - (см. рис.4.34,б).

3. Соответствующая эквивалентная система приведена на рис.4.35.

4. Записываем канонические уравнения метода сил:

.

5. Для определения , , , , воспользуемся способом Верещагина.

Определяем , . (рис.4.36)

- ;

.

Определяем (рис. 4.37).

.

Определяем (рис. 4.38).

= .

Определяем (рис. 4.39).

“X =1”

6) Определяем :

.

7) Для проверки используем условия равенства нулю прогибов на двух крайних правых опорах. Эти условия можно записать в виде интегралов Мора:

; ,

где - изгибающий момент для эквивалентной системы (рис. 4.40, а); , - изгибающие моменты для основной системы (см. рис. 4.34, б), нагруженной и (см. рис. 440, б, в). Для определения интегралов Мора можно использовать способ Верещагина (см. рис. 4.40).

Следовательно, Х₁, Х₂ определены верно.

Рис. 4.40(начало)

2. Строим эпюры и для эквивалентной системы (см. рис. 4.40,ж), представляющей собой три балочки, для каждой из которых независимо определены реакции опор.

Рис. 4.40(окончание)

.

3. Так как поперечное сечение по длине балки постоянно, условие прочности имеет вид , где изгибающий моментов в опасном сечении, равный (см. рис. 4.40, и).

Расчёт проектный, поэтому из условия прочности определяем необходимый момент сопротивления :

По таблице сортамента выбираем двутавр №12, для которого .

4.55. Для двутавровых стальных балок №40, схемы нагружения которых приведены на рис. 4.41, а-е, определить допускаемые нагрузки. Принять м, м, МПа.

4.56. Для двутавровых стальных балок, схемы нагружения которых приведены (см. рис. 4.41, ж-л, рис. 4.42, а-д), определить номер двутавра, приняв МПа.

4.57. Двутавровые неразрезные балки нагружены, как указано (см.рис. 4.42, е-и.). Подобрать номер двутавра из условия прочности Р=50кН, q=40 кН/м, МПа, Е=2 МПа. Нарисовать приблизительно изогнутые оси балок и отметить точки перегиба.

4.58. Для неразрезных балок постоянного поперечного сечения (см. рис. 4.42, к, л) подобрать из условия прочности сечения в виде двух одинаковых швеллеров. Принять материал Ст.3, МПа. Нарисовать приблизительно изогнутые оси балок и отметить положение точек перегиба.

Рис. 4.41 (окончание)

Рис. 4.42 (начало)

Рис. 4.42 (окончание)

4.59. Дюралевая балка (рис. 4.43) длиной м швеллерного сечения ( подвешена на трех стальных тягах длиной 1 м и поперечным сечением 0,1 . Балка несет груз P=5 кН, приложенный посередине. Определить усилия в тягах и в балке. , МПа.

4.60. Балка постоянной жесткости (рис. 4.44) защемлена одним концом и установлена на упругой опоре, податливость которой К. Определить максимальное напряжение в балке, если заданы P, .

Указание: податливостью упругой опоры называется ее осадка под действием силы, равной 1 Н, размерность податливости – м/Н.

4.61. Две перекрестные балки длиной , (рис. 4.45) нагружены посередине силой P. Найти распределение нагрузки между балками. Моменты инерции сечений . Материал балок одинаковый.

4.62. При каком значении x прочность трехопорной балки постоянного сечения (рис. 4.46,а) будет наибольшей? Материал сопротивляется растяжению и сжатию одинаково.

4.63^*. Доказать, что при любой нагрузке на консольной части балки АВС (см.рис. 4.46,б) изгибающий момент в заделке (сечение А) равен по модулю половине момента в сечении В, если пролет АВ свободен от нагрузок.

4.64. При каком значении силы P реакции опоры А балки (рис. 4.47) будет равна нулю? Дано q, .

4 . 65^*. Две консольные балки АВ и СD (рис. 4.48) нагружены силой Р, в точке В – каток. Жесткости при изгибе обеих балок равны. Найти силу взаимодействия между балками в точке В.

Рекомендации.

Задача решается при условии равенства перемещений точек В и D соответствующих балок, которые рассчитывают способом Мора или Верещагина согласно приведенным на рис. 4.49 расчетным схемам. Здесь Х – искомая сила взаимодействия между балками.

Ответ: .

4.66^*. Определить положение пролетных шарниров В и С (рис. 4.50), при котором прочность балки с заданными размерами будет наибольшей из расчета на прочность по нормальным напряжениям. Дано q, l.

Рекомендации

При решении данной задачи можно представленную балку с шарнирами в точке В и С рассматривать (без учета растягивающих сил), как одну консольную (в силу симметрии), например, АВ и балку ВС на двух шарнирных опорах. Условием равной прочности этих балок будет равенство их наибольших изгибающих моментов.

Ответ: а = l\3.

4.67^*. В балке, жестко заделанной двумя концами, (рис.4.51) правая опора переместилась вниз на величину Δ. Жесткость балки равна ЕJ_х. Определить опорные реакции и построить эпюры поперечных сил и изгибающих моментов (нормальную силу в сечении балки считать отсутствующей).

Рекомендации.

При составлении канонических уравнений вертикальному перемещению правой опоры Δ выбирается знак в соответствии с направлением неизвестной силы Х₁ в опоре В.

Ответ: - (направление вниз);

- (против часовой стрелки).