4.2.2. Затухающие колебания и их характеристики

Реальный колебательный контур всегда обладает активным сопротивлением R . Вследствие этого часть энергии электромагнитных колебаний превращается в тепло, а амплитуда колебаний постепенно уменьшается.

Дифференциальное уравнение затухающих колебаний на основании(4.65) и с учётом, что , , , принимает вид

. (4.73)

После замены

(4.74)

получим стандартное дифференциальное уравнение, описы- вающее затухающие колебания

. (4.75)

Здесь – коэффициент затухания, ω₀ – собственная частота свободных незатухающих колебаний (т.е. при R=0).

Решение дифференциального уравнения (4.75) имеет вид

, (4.76)

г

де , (4.77)

- частота затухающих колебаний в реальном контуре.

График затухающих колебаний представлен на рис.4.17. Амплитуда колебаний в этом случае изменяется по экспо- ненциальному закону

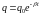, (4.78)

а период колебаний определяется выражением

. (4.79)

С увеличением R, а следовательно, и β, период затухающих колебаний растёт, стремясь к бесконечности при

. (4.80)

Это означает, что при колебательный разряд переходит в апериодический процесс (рис.4.18). Значение R_кр называется критическим сопротивлением.

Важнейшей характеристикой контура является его добротность. При малых значениях логарифмического декремента затухания, добротность контура определяется выражением:

. (4.81)

4.2.3. Вынужденные колебания в контуре. Резонанс

Для осуществления вынужденных электромагнитных колебаний нужно включить последовательно с элементами контура источник переменного напряжения, изменяющегося по гармоническому закону (рис.4.19).

U = U₀ cos ω_в t . (4.82)

Тогда формула (4.65) примет вид

. (4.83)

Произведя преобразования, получим стандартное диффе- ренциальное уравнение вынуж- денных электромагнитных колебаний.

. (4.84)

В случае установившихся колебаний решение дифферен- циального уравнения имеет

q = q₀ cos(ω_в t + ψ), (4.85)

где ψ – сдвиг фаз между зарядом на обкладках конденсатора и переменной ЭДС.

Следовательно, в установившемся режиме, вынужденные колебания происходят с частотой вынуждающего напряжения ω_в и являются гармоническими, амплитуда и фаза которых определяется выражениями

, (4.86)

. (4.87)

Резонансные кривые для заряда (напряжения на конденсаторе) аналогичны резонансным кривым при механических колебаниях (см. рис.4.13), а резонансная частота определяется по формуле (4.50).

Продифференцировав (4.85) по t, найдем силу тока в контуре

I = - q₀ ω_в sin(ω_в t + ψ) = I₀ cos(ω_в t + ψ + π/2),

где I₀ = q₀ ω_в – амплитуда тока.

Запишем это выражение в виде

I = I₀ cos(ω_в t – φ), (4.88)

где φ = -(ψ + π/2) – сдвиг фаз между током и приложенным напряжением.

Тогда в соответствии с (4.86) и (4.87)

, (4.89)

. (4.90)

Из формулы (4.90) следует, что ток отстаёт по фазе от вынуждающего напряжения в том случае, когда , и опережает, когда . При условии сдвиг фаз равен нулю, а амплитуда тока достигает максимального значения.

Разделив выражение (4.85) на емкость, получим напряжение на конденсаторе

, (4.91)

где

. (4.92)

Умножив производную функции (4.88) на L, получим напряжение на индуктивности:

(4.93)

где . (4.94)

Сопоставление формул (4.88), (4.91) и (4.93) показывает, что напряжение на емкости отстает по фазе от силы тока на π/2 , а напряжение на индуктивности опережает ток на π/2 .

Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы (рис. 4.20).

Резонансная частота для заряда и напряжения на конденса- торе равна

. (4.95)

Р

2

езонансные кривые для U_с изображены на рис.4.21 . При ω→0 резонансные кривые сходятся в одной точке с ординатой U_Cm = U₀ – напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения U_0. Максимум при резонансе получается тем выше и острее, чем меньше β = R/2L.

Резонансные кривые для силы тока изображены на рис. 4.22. Амплитуда силы тока имеет максимальное значение при .

R₁ < R₂ < R₃

R₁

R₂

R₃

Рис. 4.21

Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура

. (4.96)

При ω→0, I = 0, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

Резонансные свойства контура характеризует доброт- ность Q, которая показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение, т.е.

(4.97)

При малых затуханиях ω _рез ≈ ω₀ и

(4.98)

Таким образом, добротность обратно пропорциональна активному сопротивлению контура.

Добротность контура определяет остроту резонансных кривых. На рис. 4.23 изображена одна из резонансных кривых для силы тока в контуре. Частоты ω₁ и ω₂ соответствуют току .

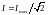Рис.4.23

Относительная ширина резонансной кривой равна величине обратной добротности контура, т. е.

(4.99)

Рис. 4.23

5

Явление резонанса используют для выделения из сложного напряжения, равного сумме нескольких синусо- идальных напряжений, нужной составляющей. Настроив контур (посредством изменения R и C) на требуемую частоту _i , можно получить на конденсаторе напряжение в Q раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляю- щими, будет слабым. Таким образом, осуществляется, например, настройка радиоприёмника на нужную длину волны.