2.3. Особенности моделирования механического контакта при восстановлении методом гальвано контактной обработки

В связи стем, что как указывалось ранее, процесс восстановления деталей методом ГКО осуществляется при наличии механического воздействия на покрытие в процессе его осаждения, большой интерес представляет модель, позволяющая заранее оценивать степень и скорость деформации покрытия, что позволит заранее определить силовые режимные параметры воздействия на объект и исключить появление брака из-за некачественного покрытия, получаемого в процессе восстановления.

Плотность металла в процессе пластической деформации меняется весьма незначительно [3]. Поэтому обычно принимают следующее условие: объем пластически деформированного элементарного объема остается постоянным, т.е. объем тела до пластической деформации равен его объему после деформации.

Пластическая деформация осаждаемого кристалла всегда сопровождается его упругой деформацией [14]. Следовательно, размеры тела в конечный момент его нагружения отличаются от его размеров при снятии нагрузки.

В качестве деформируемого объема рассмотрим параллелипипед, подвергаемый деформации сжатия с ребрами расположенными параллельно пространственной системе координат с исходными размерами до деформации X_и Y_и Z_и. После деформации размеры рассматриваемого параллелепипеда станут X_д Y_д Z_д. (рис. 2.1)

Исходя из условия постоянства объема при деформировании [40] можно записать

(2.4)

откуда

(2.5)

Прологарифмировав все части уравнения (2.5) с помощью натуральных логарифмов, получим

(2.6)

или

(2.7)

где

(2.8)

Величины _х, _y, _z показывают действительную степень деформации элементарного объема материала.

Индексы при значении  показывают по направлению какой координатной оси рассматривается деформация.

В нашем конкретном случае элементарный объем материала подвергается сжатию, т.е. ребро Z уменьшается, а ребра X и Y увеличиваются (рис 2.2). Следовательно, принимая во внимание формулы (2.8) можно утверждать, что деформация _z будет отрицательной, а деформации _x и _y положительными.

Для представления логарифмической степени деформации надо взять интеграл бесконечно малого приращения рассматриваемого размера тела или его элемента, отнесенного к его величине в каждый данный момент деформации

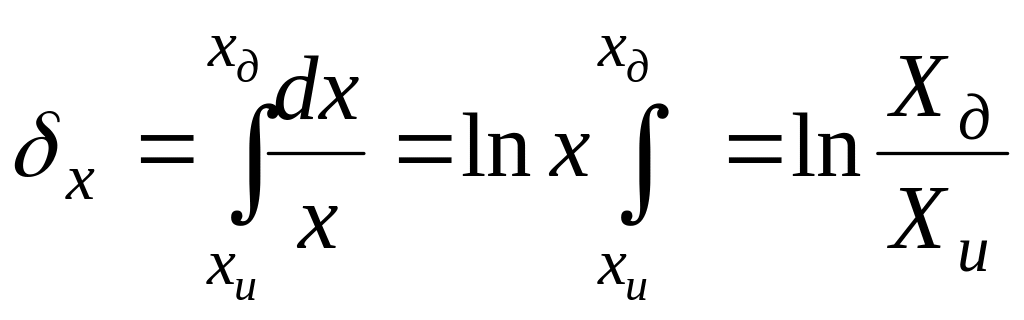(2.9)

На основании уравнения (2.6) можно сделать следующие выводы:

1. При пластической деформации алгебраическая сумма логарифмических степеней деформации по трем взаимно перпендикулярным направлениям равна нулю.

2. Одна из степеней деформации имеет знак, противоположный знаку двух других, а по абсолютной величине равна их сумме, т.е. максимальна по абсолютной величине.

Рис.2.2. Схема деформации растущих кристаллов

С другой стороны большой интерес представляет выражение степени деформации как отношение приращения размера к начальному размеру:

(2.10)

В связи с тем, что восстанавливаемая деталь имеет различные пространственные погрешности формы поверхности, не представляется возможным обеспечить равномерное давление инструмента на восстанавливаемую поверхность, а в случае восстановления по методу ГКО с применением инструмента НС-1 это и нужно. Учитывая вышеизложенное, можно с уверенностью утверждать, что деформации в различных точках тела могут быть различны, т.е. деформация может быть неравномерной. Формулы (2.8) и (2.10) дают лишь усредненные степени деформации данного тела или его части.

Определение значений деформаций в окрестностях конкретной точки будет рассмотрено позже.

Величины  и  связаны между собой:

Для удобства дальнейшей работы разложим ln(1+_x) в ряд

Как видно из полученного выражения, этот ряд при _х  1 сходящийся. Отбросив все члены, кроме первого, получим _х  _х.

В связи с тем, что усилия инструмента при его воздействии на осаждаемое покрытие крайне незначительно, можно считать, что в данном случае имеет место малая деформация (степень деформации менее 0,01). По [15] для малых деформаций

 = (2.11)

и соответственно

(2.12)

Умножив все члены уравнения (2.7) на объем V деформируемого тела, получим

(2.13)

а для малых деформаций

(2.14)

Таким образом, сумма произведений объема на логарифмические степени деформаций (сминаемый объем) по взаимно перпендикулярным направлениям равна нулю.

Рассмотрим математически образование деформируемого объема материала. Пусть в некоторый момент времени рассматриваемый элементарный объем материала в виде параллелепипеда имеет размер Z по оси z, который в следующий момент при воздействии на него инструмента деформируется на некоторую величину, получая отрицательное приращение dz (рис. 2.3).

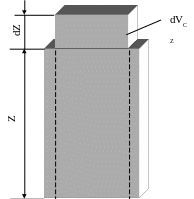
Рис.2.3 Схема деформации элементарного объема

Элементарный сминаемый объем определяется выражением:

(2.15)

где F_z – площадь нормальных сечений осаждаемого покрытия в каждый конкретный момент процесса деформации. Тогда

(2.16)

если F_z = V/z

то

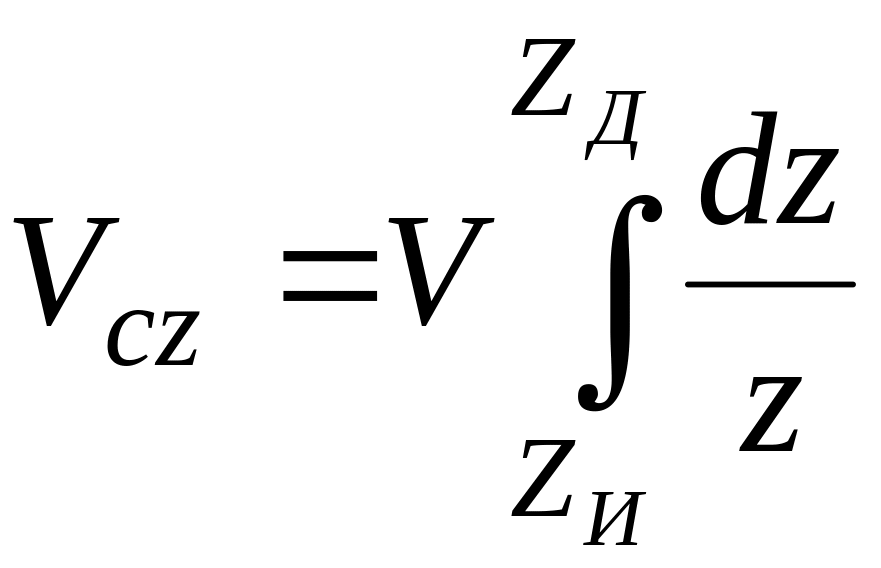(2.17)

Интегрируя, получим

(2.18)

В общем виде это выражение запишется так

V_c = V (2.19)

Для малых деформаций  = , следовательно

V_c = V (2.20)

Физический смысл сминаемого объема поясняет рис. 2.4.

Подобная схема деформации для определения степени и скорости деформации была выбрана не случайно. Она была представлена в работах [83, 84] и экспериментально проверена в работах [19; 77]. Однако в вышеперечисленных работах ставилась задача проверить влияние усилия прижима на остаточные напряжения, возникающие в осаждаемом покрытии. Исследования влияния усилия деформации покрытия, получаемого в процессе восстановления изношенных поверхностей детали, на степень и скорость деформации вышеназванного покрытия не рассматривались. Однако в [15] отмечается, что превышение скорости и степени деформации различных металлов может приводить к возникновению в них различных дефектов, таких как трещины, сколы и т.д.

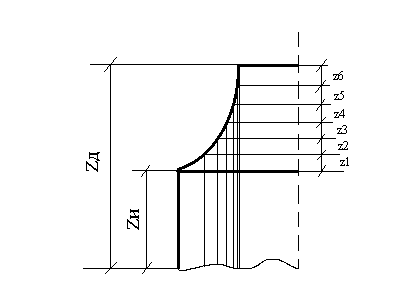
Рис.2.4. Схема послойной деформации растущих слоев осадка

Из написанного ранее выражения (2.5) следует

(2.21)

так как

Y_иZ_и = F_их и Y_дZ_д = F_дх

где F_их и F_дх – площади соответственно нормальных к оси х сечений тела до и после деформации.

Учитывая вышеизложенное представляется возможным выразить степени деформации и сминаемые объемы не только через линейные размеры, но и через площади сечений, нормальных к оси координат, в направлении которой рассматривается степень деформации и сминаемый объем:

(2.22)

(2.23)

Аналогично можно получить выражения для вычисления степеней деформации по направлениям осей координат y и z.

В общем виде можно записать

(2.24)