А.П. Бырдин, в.И Кузнецова, в.С. Прач, а.А Сидоренко о распространении плоских термоупругих волн в наследственно-упругой среде
В работе изучается влияние совместного действия полей деформации и температуры на распространение плоских волн малой амплитуды в наследственно-упругой среде с нелинейным определяющим соотношением. Установлено влияние нелинейной наследственности на эволюцию термоупругих волн
Как
известно [1], поле температур не оказывает
влияние на волны искажения, но существенно
влияет на эволюцию волн расширения,
которые и рассматриваются в настоящей
работе. Предполагаем, что направление
распространения волны совпадает с
направлением оси
.
Тогда первая компонента вектора
перемещений будет зависеть только от
этой координаты
.
Для изучения взаимодействия температурного поля, нелинейности по деформации и дисперсии, вызванной диссипативными процессами в изотропной среде, рассмотрим вязкоупругий материал, уравнение состояния которого в одномерном случае имеет вид
,
(1)
где
,
- напряжение и деформация;
- изотермические модули Юнга и объемного
расширения;
- коэффициент Пуассона;
- параметр, характеризующий нелинейность;
- средний коэффициент линейного теплового
расширения
,
,
,
-
параметр, определяемый моделью нелинейного
члена в (1);
-
истинный коэффициент линейного теплового
расширения;
- начальная температура среды. Операторы
,
входящие в определяющее соотношение
(1), определены правилом
,
,
,
(2)
где
- дельта-функция Дирака,
-
времена релаксации линейной и нелинейной
составляющих напряжения,
- дефект модуля упругости. Функции
и
,
входящие в ядра наследственности (2),
моделируются на основе экспериментов
в опытах на релаксацию и должны монотонно
убывать с ростом аргументов в соответствии
с принципом затухающей памяти [2].
Рассмотрим распространение плоских упругих волн малой, но конечной аплитуды в нелинейной наследственно-упругой среде с учетом термомеханического сопряжения. Введем безразмерные величины
,
,
,
,
(3)
где - массовая плотность материала. В дальнейшем безразмерные переменные будем записывать в прежних обозначениях, отбрасывая штрихи над буквами.
Уравнение движения в деформациях и уравнение энергии в безразмерных переменных имеет вид
,
(4)
(5)
где
волновой оператор
,
оператор диффузии
и оператор
определены выражениями
,
,
,
,
,
-
массовая теплоемкость при постоянных
деформациях,
- коэффициент теплопроводности, ядро
интегрального оператора
в (4) имеет вид
.
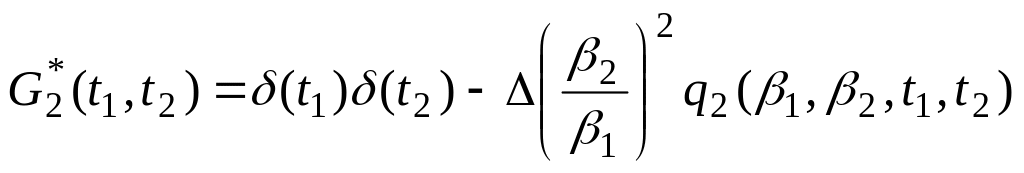Уравнение теплопроводности (5), учитывающее диссипативный разогрев среды, записано в предположениях принятых в работе [3].
Сосредоточим далее внимание на изучении волн деформации, исключив из уравнения движения температурный член на основании (5). Отметим, что при обработке опытных данных обычно используются функции наследственности либо соответствующие модели стандартного линейного тела, либо слабосингулярные ядра Колтунова или Работнова [2], которые являются экспоненциально убывающими. Будем предполагать, что изменение производных деформации происходит значительно медленнее изменений ядра интегрального оператора, так что можно разложить деформации в ряд по малому запаздыванию с удержанием двух первых членов разложения
,
,
,
(6)
где
точкой над буквой обозначена производная
по
,
штрихом – производная по
.
В результате проведения описанной выше процедуры получим приближенное уравнение движения в виде
(7)
где
,
,
.
Точное решение нелинейного интегро-дифференциального уравнения (7) невозможно получить в замкнутом виде. При естественном предположении малости нелинейных членов его решение можно построить в виде ряда полилинейных функционалов (4). Качественное поведение решения этого уравнения можно получить, воспользовавшись асимптотическими методами.
В
дальнейшем будем предполагать, что
дефект модуля упругости и коэффициент
нелинейности в уравнении (7) являются
малыми величинами. Известно также [5],
что температура саморазогрева
вязко-упругой среды из-за внутренней
диссипации энергии изменяется во времени
весьма медленно. В соответствии с этим
коэффициент связности предполагается
в дальнейшем величиной второго порядка
малости по параметру
.
Для
получения приближенного решения
уравнения (7) воспользуемся методом
медленно изменяющегося профиля [6].
Поскольку невозмущенное уравнение,
соответствующее уравнению (7), имеет
решение в виде волны, распространяющейся
со скоростью
,
то ограничившись волной, распространяющейся
вдоль положительного направления оси
,
предполагаем профиль волны медленно
изменяющимся в пространстве
.
(8)
Переходя
к сопровождающей волну системе координат
(
,
и ограничившись при построении уравнения первым приближением по малому параметру, получим следующее нелинейное дифференциальное уравнение
.
(9)
Уравнение
(9), описывающее в принятом приближении
поведение квазипростой волны, является
уравнением Бюргерса [7]. Простейшей
заменой независимых переменных
,
уравнение приводится к стандартному
виду. Как известно [8], уравнение Бюргерса
при помощи подстановки Коула-Хопфа,
имеющей в данном случае вид
(10)
переходит относительно новой функции в линейное уравнение диффузии, замкнутое решение которого известно. Уравнение (9) отражает как эффекты нелинейного распространения волн, так и эффекты влияния диссипации на деформацию профиля волны, вызванной нелинейностью, производимые членом в правой части уравнения.
Используя
соотношение Коула-Хопфа (10), из решения
уравнения диффузии с условием при
вида
,
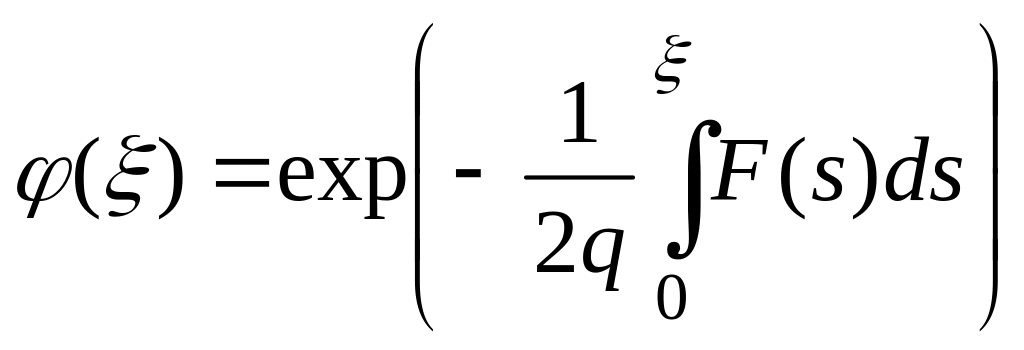где
- заданная функция,
,
,
можно получить решение уравнения (9) в следующей форме
,
(11)
где
,
,
.
Приближенное решение (11) уравнения (7), описывающее распространение волн в физически нелинейной и диссипативной среде, включает заданную форму волны в фиксированной плоскости. Для уравнения (9), как известно [8], можно получить и другие типы решений, например, решение Тейлора, описывающее стационарную волну, крутизна фронта которой зависит от величины отношения параметров при диссипативном и нелинейном членах уравнения.
Отметим в заключении: отличные от принятых в этой работе предположения относительно величин параметров и типов задач, поставленных для системы уравнений (4), (5), приводят к приближенным уравнениям для деформаций, сводящимся к уравнению Кортевега - де Вриза, либо к уравнению Кортевега - де Вриза – Бюргерса]. В первом случае на эволюцию нелинейных волн преобладающее влияние оказывает эффект дисперсии, во втором – учитывается совместное влияние диссипации и дисперсии.
Литература
1. Новацкий В. Динамические задачи термоупругости. – М.: Мир, 1970. – 256 с.
2. Работнов Ю.Н. Элементы наследственной механики твердых тел. – М.: Наука, – 1977. – 384 с.
3. Карнаухов В.Г. О распространении вязко-упругих волн конечной амплитуды // Прикл. Механика, 1972, т. 9, №4. – с. 36 – 44.
4. Бырдин А.П., Розовский М.Н. О волнах деформации в нелинейной наследственно-упругой среде // Изв. АН СССР. Механика твердого тела, 1984, №4. – с. 100-104.
5. Карнаухов В.Г., Киричок И.Ф. К термомеханической теории трехслойных ортотропных оболочек с вязко-упругим заполнителем // Прикл. Механика, 1983, т.19, №7. – с. 31 – 37.
6. Ланда П.С. Автоколебания в распределенных системах. – М.: Наука, 1983. – 320 с.
7. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. – М.: Наука, 1986. – 736 с.
8. Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М.: Мир, 1988. – 694 с.
Воронежский государственный технический университет
Донецкий политехнический институт (г. Донецк, Украина)
УДК 624.073