
- •Математические методы исследования операций и теории иГр
- •Введение
- •Глава 1. Задачи линейного программирования
- •1. Постановка задачи линейного программирования (злп)
- •2. Графический метод решения злп
- •3. Симплекс – метод решения злп
- •Метод искусственного базиса
- •Двойственные злп
- •Двойственный симплекс-метод
- •Алгоритм двойственного симплекс-метода.
- •Метод ветвей и границ решения задачи цлп
- •Алгоритм метода ветвей и границ
- •Оптимальность по Парето
- •Множество Парето
- •Постановка задачи
- •Метод идеальной точки
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 2. Теория игр
- •1. Основные понятия теории игр
- •Принцип доминирования
- •2. Задачи теории игр и линейное программирование
- •3. Игры с природой
- •Применение матричных игр в прикладных задачах
- •Переговоры о заключении контракта между профсоюзом и администрацией
- •Локальный конфликт
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 3. Имитационное моделирование
- •Основные понятия
- •Типы имитационных моделей.
- •Принципы построения дискретных имитационных моделей
- •Метод Монте-Карло (метод статистических испытаний)
- •Применение имитационных моделей в системах массового обслуживания
- •Вопросы для повторения.
- •Глава 4. Сетевое планирование
- •1. Сетевой график
- •Оптимизация пути на сети
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Заключение
- •Библиографический список
- •Оглавление
- •3 94026 Воронеж, Московский просп., 14
Двойственный симплекс-метод
Можно применять при решении задач ЗЛП, свободные члены системы уравнений, которой могут быть любыми числами.
Рассмотрим задачу:
![]() (1)
(1)
![]() (2)
(2)
![]()
 (3)
(3)
 ,
,
 ,
… ,
,
… ,
 ,
,
 ,
… ,
,
… ,
 ,
,

и среди чисел
среди чисел
![]() имеются
отрицательные.
имеются
отрицательные.
О
пределение.
Решение
![]() системы линейных уравнений ( 2 ),
определяемых базисом
системы линейных уравнений ( 2 ),
определяемых базисом
![]() называется
псевдопланом задачи ( 1 ) – ( 3 ),
если
называется
псевдопланом задачи ( 1 ) – ( 3 ),
если
![]()
Т
еорема
1. Если в псевдоплане
,
определяемом базисом
есть хотя бы одно отрицательное число
![]() <0,
такое, что все
<0,
такое, что все
![]() то
задача (1) – ( 3 ) вообще не имеет планов.
то
задача (1) – ( 3 ) вообще не имеет планов.
Теорема 2. Если в псевдоплане
,определяемом
базисом
имеются
отрицательные числа
<
0, такие, что для любого из них существуют
числа
![]() <
0, то можно перейти к новому псевдоплану,
при котором значение целевой функции
задачи (1) – (3) не уменьшится.
<
0, то можно перейти к новому псевдоплану,
при котором значение целевой функции
задачи (1) – (3) не уменьшится.
Алгоритм двойственного симплекс-метода.
Находят псевдоплан задачи.
Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.
Выбирают разрешающую строку с помощью определения наибольшего по модулю отрицательного числа столбца вектора
 и разрешающий столбец с помощью
нахождения наименьшего по модулю
отношения элементов
и разрешающий столбец с помощью
нахождения наименьшего по модулю
отношения элементов
 -ой
строки к соответствующим отрицательным
элементам разрешающей строки.
-ой
строки к соответствующим отрицательным
элементам разрешающей строки.Находят новый псевдоплан и повторяют все действия, начиная с п. 2.
Пример 1. Найти максимальное значение функции
![]()
при условиях
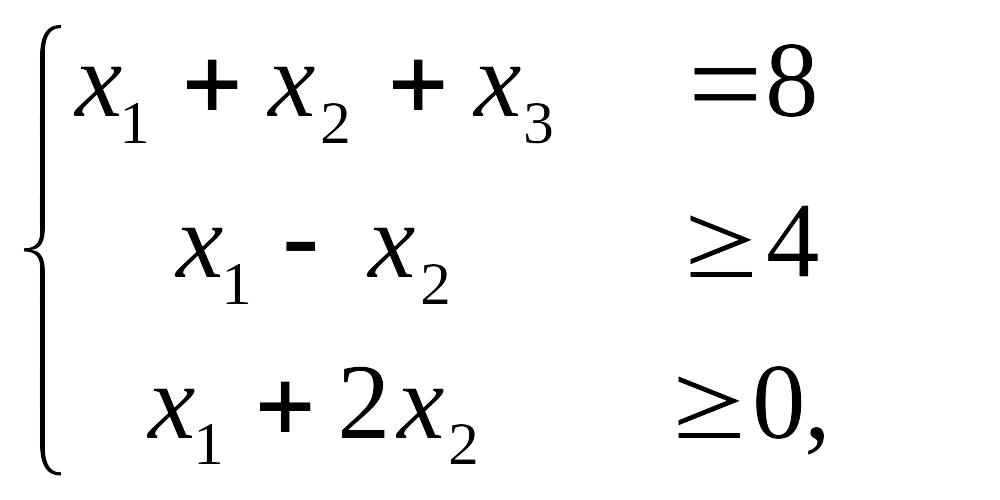
![]()
Решение. Запишем исходную ЗЛП в форме основной задачи: найти max функции
п![]() ри
условиях
ри
условиях

![]()
Умножив второе и третье уравнения системы ограничений на (-1), переходим к следующей задаче:
(1)
при условиях
![]()
 (2)
(2)
(3)
Результаты вычислений оформим в виде последовательности симплекс – таблиц.
|
Базис |
|
|
1 |
1 |
2 |
0 |
0 |
|
|
|
|
|
||||
1 |
|
2 |
8 |
1 |
1 |
1 |
0 |
0 |
2 |
|
0 |
-4 |
-1 |
1 |
0 |
1 |
0 |
3 |
|
0 |
-6 |
-1 |
-2 |
0 |
0 |
1 |
4 |
|
|
16 |
1 |
1 |
0 |
0 |
0 |
1 |
|
2 |
5 |
½ |
0 |
1 |
0 |
½ |
2 |
|
0 |
-7 |
-3/2 |
0 |
0 |
1 |
½ |
3 |
|
1 |
3 |
½ |
1 |
0 |
0 |
-1/2 |
4 |
|
|
13 |
½ |
0 |
0 |
0 |
½ |
1 |
|
2 |
8/3 |
0 |
0 |
1 |
1/3 |
2/3 |
2 |
|
1 |
14/3 |
1 |
0 |
0 |
-2/3 |
-1/3 |
3 |
|
1 |
2/3 |
0 |
1 |
0 |
1/3 |
-1/3 |
4 |
|
|
32/3 |
0 |
0 |
0 |
1/3 |
2/3 |
Выбрав в качестве базиса векторы
![]() составим
симплексную таблицу для исходной задачи
(1) – (3). Вычисляем:
составим
симплексную таблицу для исходной задачи
(1) – (3). Вычисляем:
![]()
Так как в столбце вектора
имеются отрицательные числа (-4) и (-6), а
в 4-ой строке отрицательных чисел нет,
то в соответствии с алгоритмом
двойственного симплекс-метода переходим
к новой симплекс-таблице ( в данном
случае это можно сделать, т. к. в строках
векторов
и
имеются отрицательные числа. Если бы
они отсутствовали в одной из строк, то
задача была бы неразрешима). Вектор,
исключаемый из базиса, определяется
наибольшим по модулю отрицательным
числом, стоящим в столбце вектора
В данном случае это число (-6). Следовательно,
из базиса исключаем вектор
.
Чтобы определить, какой вектор необходимо
ввести в базис, находим
 ,где
,где
![]() .
Имеем:
.
Имеем:
![]() . Значит в базис вводим вектор
.
Переходим к новой симплекс таблице. Т.
к. в столбце вектора
последней симплекс-таблицы стоит число
(-7), то рассмотрим элементы 2-ой строки.
Среди этих чисел есть одно отрицательное
(-3/2). Если бы такое число отсутствовало,
то исходная задача была бы неразрешима.
В данном случае переходим к новой
симплекс-таблице. Как из неё видно,
найден оптимальный план исходной задачи
. Значит в базис вводим вектор
.
Переходим к новой симплекс таблице. Т.
к. в столбце вектора
последней симплекс-таблицы стоит число
(-7), то рассмотрим элементы 2-ой строки.
Среди этих чисел есть одно отрицательное
(-3/2). Если бы такое число отсутствовало,
то исходная задача была бы неразрешима.
В данном случае переходим к новой
симплекс-таблице. Как из неё видно,
найден оптимальный план исходной задачи
![]() при
этом плане максимальное значение целевой
функции равно
при
этом плане максимальное значение целевой
функции равно
![]() .
.
Пример 2. Найти максимальное значение функции
![]()
при условиях

Решение. Умножая первое и третье уравнения системы ограничений на (-1), в результате приходим к задаче определения максимального значения функции
при условиях

Процесс вычислений оформляем в виде симплекс-таблиц.
|
Базис |
|
|
2 |
3 |
0 |
5 |
9 |
|
|
|
|
|
||||
1 |
|
0 |
-12 |
2 |
-1 |
1 |
0 |
0 |
2 |
|
5 |
10 |
1 |
2 |
0 |
1 |
0 |
3 |
|
0 |
-18 |
-3 |
2 |
0 |
0 |
1 |
4 |
|
|
50 |
3 |
7 |
0 |
0 |
0 |
1 |
|
0 |
-24 |
0 |
1/3 |
1 |
0 |
2/3 |
2 |
|
5 |
4 |
0 |
8/3 |
0 |
1 |
1/3 |
3 |
|
2 |
6 |
1 |
-2/3 |
0 |
0 |
-1/3 |
4 |
|
|
32 |
0 |
9 |
0 |
0 |
1 |
![]() .
.
Так как в столбце вектора имеется одно отрицательное число (-24), а в строке вектора нет отрицательных чисел, то исходная задача не имеет решения.
Целочисленное (дискретное) линейное программирование (ЦЛП).
Некоторые ЗЛП требуют целочисленного решения. К ним относятся задачи по производству и распределению неделимой продукции (выпуск стаканов, телевизоров, автомобилей и т.д.).
В общем виде математическая модель задачи ЦЛП имеет вид:
![]() (1)
(1)
при ограничениях:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Метод Гомори.
Используя симплекс-метод, находят решение задачи (1) - (3) без учёта требования целочисленности переменных. Если среди компонентов оптимального плана нет дробных чисел, то найденный план является оптимальным планом задачи ЦЛП
(1) - (4).
Если в оптимальном плане задачи (1) - (3) переменная xj принимает дробное значение, то к системе уравнений (2) добавляют неравенство
![]() (5)
(5)
и находят решение задачи (1) - (5).
В неравенстве (5)
![]() и
и
![]() – преобразованные исходные величины
aij и
bi,
значения которых взяты из последней
симплекс-таблицы, а
– преобразованные исходные величины
aij и
bi,
значения которых взяты из последней
симплекс-таблицы, а
![]() и
и
![]() - дробные части чисел (под дробной частью
некоторого числа а понимается наименьшее
число b
- дробные части чисел (под дробной частью
некоторого числа а понимается наименьшее
число b![]() 0
: a - b
0
: a - b![]() Z).
Z).
Если в оптимальном плане задачи (1) - (3) дробные значения принимают несколько переменных, то дополнительное равенство (5) определяется наибольшей дробной частью.
Используя двойственный симплекс-метод, находят решение задачи, получающееся из задачи (1) - (3) в результате присоединения дополнительного ограничения.
В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (1) - (4) или установления её неразрешимости.
Пример. Методом Гомори найти максимальное значение функции
![]() (6)
(6)
при ограничениях
![]() (7)
(7)
![]() (8)
(8)
![]() . (9)
. (9)
Дать геометрическую интерпретацию решения задачи.
Решение.
Для определения оптимального плана задачи (6) - (9) сначала находим симплекс-методом оптимальный план задачи (6) -(8).
i |
базис |
Сб |
Р0 |
3 |
2 |
0 |
0 |
0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
||||
1 |
Р3 |
0 |
13 |
1 |
1 |
1 |
0 |
0 |
2 |
Р4 |
0 |
6 |
1 |
-1 |
0 |
1 |
0 |
3 |
Р5 |
0 |
9 |
-3 |
1 |
0 |
0 |
1 |
4 |
|
|
|
-3 |
-2 |
0 |
0 |
0 |
1 |
Р3 |
0 |
7 |
0 |
2 |
1 |
-1 |
0 |
2 |
Р1 |
3 |
6 |
1 |
-1 |
0 |
1 |
0 |
3 |
Р5 |
0 |
27 |
0 |
-2 |
0 |
3 |
1 |
4 |
|
|
18 |
0 |
-5 |
0 |
3 |
0 |
1 |
Р2 |
2 |
7/2 |
0 |
1 |
1/2 |
-1/2 |
0 |
2 |
Р1 |
3 |
19/2 |
1 |
0 |
1/2 |
1/2 |
0 |
3 |
Р5 |
0 |
34 |
0 |
0 |
1 |
2 |
1 |
4 |
|
|
71/2 |
0 |
0 |
5/2 |
1/2 |
0 |
Найденный оптимальный план Х = (19/2;7/2; 0;
0; 34) задачи (6)-(8) не является оптимальным
планом задачи (6) - (9), т.к. x1,
x2
![]() .
При этом дробные части этих чисел равны
между собой. Поэтому для одной из этих
переменных составляется дополнительное
ограничение. Составим, например, такое
ограничение для переменной x2.
.
При этом дробные части этих чисел равны
между собой. Поэтому для одной из этих
переменных составляется дополнительное
ограничение. Составим, например, такое
ограничение для переменной x2.
![]()
Таким образом, к системе ограничений задачи (6) - (8) добавляем неравенство
![]() или
или
![]() т.е.
т.е.
![]()
В конечном виде:
![]() .
.
С учётом последнего уравнения решаем полученную ЗЛП двойственным симплекс-методом.
i |
базис |
Сб |
Р0 |
3 |
2 |
0 |
0 |
0 |
0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
||||
1 |
Р2 |
2 |
7/2 |
0 |
1 |
1/2 |
-1/2 |
0 |
0 |
2 |
Р1 |
3 |
19/2 |
1 |
0 |
1/2 |
1/2 |
0 |
0 |
3 |
Р5 |
0 |
34 |
-0 |
0 |
1 |
2 |
1 |
0 |
4 |
Р6 |
0 |
-1 |
0 |
0 |
-1 |
-1 |
0 |
1 |
5 |
|
|
71/2 |
0 |
0 |
5/2 |
1/2 |
0 |
0 |
1 |
Р2 |
2 |
4 |
0 |
1 |
1 |
0 |
0 |
-1/2 |
2 |
Р1 |
3 |
9 |
1 |
0 |
0 |
0 |
0 |
1/2 |
3 |
Р5 |
0 |
32 |
0 |
0 |
-1 |
0 |
1 |
2 |
4 |
Р4 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
-1 |
5 |
|
|
35 |
0 |
0 |
2 |
0 |
0 |
1/2 |
θo=min![]() .
.
X* = (9;4;0;1;32) - оптимальный план исходной задачи ЦЛП.
Fmax=35.
Дадим геометрическую интерпретацию решения задачи. Для этого запишем исходную задачу в виде общей ЗЛП:
![]()
![]()

Областью допустимых решений задачи (6) - (8) является многоугольник ОАВСД. Из рисунка видно, что максимальное значение целевая функция принимает в точке С(19/2; 7/2), т.е. что X=(19/2; 7/2; 0; 0; 34) является оптимальным планом.
Так как X = (19/2; 7/2; 0; 0; 34) не
является оптимальным планом задачи (6)
- (9), то вводится дополнительное ограничение
![]() .
Выразим переменные x3
и x4 из первых двух
уравнений системы (7).
.
Выразим переменные x3
и x4 из первых двух
уравнений системы (7).
![]()
Подставим полученные значения в неравенство (10).

Этому неравенству соответствует полуплоскость, ограниченная прямой x1 = 9, отсекающей от многоугольника ОАВСД треугольник EFC.
Как видно из рисунка, ОДР полученной задачи является многоугольник ОАВЕFД. В точке Е(9;4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки Е - целые числа и неизвестные х3, х4, х5 принимают целочисленные значения при подстановке в уравнения системы (7) значений x1 = 9 и х2 = 4, то X* = = (9; 4; 0; 1; 32) является оптимальным планом задачи (6) - (9).
