6. Ряды Фурье

Другим важным классом функциональных рядов являются ряды Фурье. Пусть произвольное фиксированное положительное число. Каждой функции , интегрируемой на отрезке , можно поставить в соответствие тригонометрический ряд вида

, (26)

коэффициенты которого вычисляются по формулам

, , , (27)

Такой тригонометрический ряд называется рядом Фурье функции , а коэффициенты коэффициентами Фурье этой функции.

Ответ на вопрос о сходимости ряда Фурье даёт следующая теорема.

Теорема. Пусть функция кусочно-дифференцируема на отрезке . Тогда ряд Фурье функции в каждой точке сходится и его сумма равна

В частности, в точках непрерывности функции её ряд Фурье сходится к значению функции в этой точке. В точках и ряд также сходится и имеет своей суммой число

Таким образом, во всех точках , в которых функция непрерывна, справедливо равенство

Отметим ещё, что сумма ряда Фурье кусочно-дифференцируемой на отрезке функции является периодической функцией, определенной на всей вещественной оси.

Для четных и нечетных функций коэффициенты ряда Фурье имеют специальный вид.

Для четных функций коэффициенты а коэффициенты могут быть вычислены по формулам

, (28)

Для нечетных функций , а коэффициенты могут быть найдены по формулам

, . (29)

Пример 17. Разложить в ряд Фурье функцию на отрезке .

Так как функция нечетная, то воспользуемся формулами (29) при . Получаем:

, ,

.

Подставив найденные коэффициенты Фурье в формулу (26), получим ряд Фурье для функции :

.

Функция непрерывна и кусочно-дифференцируема на отрезке , и в силу приведенной теоремы при справедливо равенство

.

В точках сумма ряда равна 0, т.е. величине

, и не совпадает со значениями разлагаемой функции:

7. Применение рядов Фурье

Ряды Фурье являются эффективным средством для решения уравнений математической физики. В частности, при решении волнового уравнения

, (30)

описывающего малые поперечные колебания упругой струны длины , закрепленной на концах. Здесь координата точки струны , переменная времени , искомая функция удовлетворяет граничным условиям

, , (31)

и начальным условиям

, , . (32)

Граничные условия обеспечивают закрепление струны на концах, функция задает начальное положение струны в момент времени , а функция - начальную скорость (по вертикали) в каждой точке . Используя ряды Фурье, можно получить решение в виде ряда

, (33)

где коэффициенты , находятся по формулам

, , (34)

Наконец, решение уравнения теплопроводности

(35)

для стержня длины при начальном распределении температуры в стержне

, , (36)

и условии теплоизолированности концов

, , (37)

задается формулой

, (38)

где коэффициенты находятся по формулам

, . (39)

Пример 18. Струна длины в начальный момент времени оттянута в точке на расстояние вверх. Найти решение уравнения колебаний закрепленной струны, для которой , если она начинает колебаться из состояния покоя.

Решение. В начальный момент времени струна имеет форму треугольника с вершиной в точке (рис. 1).

Уравнение стороны ОА, поскольку угловой коэффициент равен 1, будет . Составим уравнение стороны АВ:

, .

Таким образом,

Так как струна начинает колебаться из состояния покоя, то

.

Подставив , , в формулу (33), получим:

.

По формулам (34) найдем коэффициенты и . Коэффициент , так как подынтегральная функция тождественно равна 0, и коэффициент

(интегрируем по частям по формуле )

.

Подставив найденные значения , в формулу для , получим:

.

Это выражение можно записать в более простом виде, если заметить, что

На тригонометрическом круге всем углам вида (при всех возможных ) соответствуют четыре точки (рис. 2);

отметим, что аналогично

Следовательно, ответ можно записать в виде

.

Пример 19. Пусть в начальный момент времени распределение температуры в стержне длины 2 задается по закону треугольника (см. рис. 1), и концы стержня теплоизолированы. Найти распределение температуры стержня, если коэффициент температуропроводности .

Решение. Так же, как и при решении примера 18, найдем, что

Подставив , в формулу (38), получим:

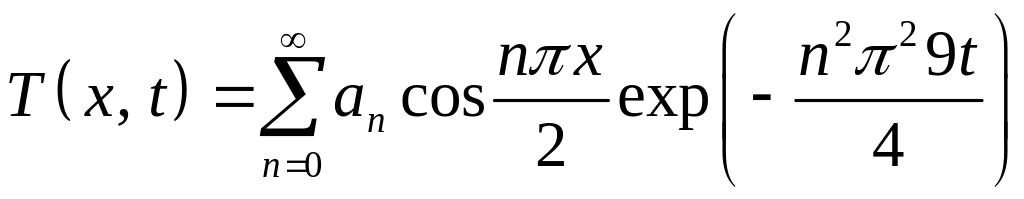, (40)

где коэффициенты вычисляются по формуле (39) при :

(интегрируем по частям по формуле )

Заметим теперь, что

.

Осталось найти коэффициент по формуле (39) при , .

.

Подставив найденные значения в формулу (40) для , (сначала , а затем ), получим распределение температуры в каждой точке стержня в любой момент времени :

.