
Учебное пособие 2032
.pdf
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
L |
L |
|
|
|
1 |
f c |
i |
|
x |
. |
|
|
|
|
|
||||||
|
|
|
n |
i |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Длина дуги AB по определению равна |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|
|||||
|
L |
lim |
L |
|
|
lim |
|
1 |
|
f |
c |
x |
i |
|
||||||||||
|
|
n |
|
i |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Li 0 i 1 |
|
|
|
|
0 i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
max |
max |
Li |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Поскольку |
по |
условию |
|
|
f |
x |
|
непрерывна, |
то |
||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегральная |
сумма |
1 |
|
f |
|
ci |
2 |
|
|
xi |
|
составлена |
|
для |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непрерывной функции, а значит, имеет предел при |
|
xi |
0 |
|||||||||||||||||||||
( xi |
0 при |
Li |
0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dx . |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
L |
1 |
|
f |
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть уравнение кривой АВ задано в параметрической |
|||||||||||||||||||||||
форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x t , |
|
|
t |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y |
y t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
x x y |
и y |
y t |
являются непрерывными функциями |
||||||||||||||||||||
вместе со своими производными, |
x |
|
|
|
a , |
x |
|
|
b , |
то длина |
||||||||||||||
дуги находится с помощью замены переменной в интеграле
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
t |
|
|
||
|
|
|
x 2 dx . Тогда dx |
|
|
|
|
|
|
|
||||||||||
1 |
|
f |
|
x |
t dt, f x |
, а |
||||||||||||||
|
|
|
||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
t |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
y t |
2 |
|
|
|
|
|
|
||
|
|
|
f x 2 dx |
|
|
|
|
|
|
x t 2 y t 2 dt. |
||||||||||
L |
1 |
1 |
|
|
x t dt |
|
|
|||||||||||||
|
x |
t |
|
|
||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 9.5. Вычислить длину линии, заданной |
||||||||||||||||||
параметрически: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
cos3 t, 0 |
t |
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y |
sin3 t, |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
171

Решение: Найдем производные x (t)  3cos2 t
3cos2 t  sint и
sint и
|
y (t) |
3sin2 t |
cost . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
L |
|
|
|
|
|
9cos4 t sin2 t 9sin4 t cos2 tdt |
9cos2 t sin2 t cos2 t |
sin2 t |
|
|
|
|
|
||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 cost sintdt |
3 |
|
2 sin 2tdt |
|
|
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|||||||||||||
3 |
|
|
|
cos2t |
|
2 |
|
cos |
cos0 |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
2 0 |
|
4 |
|
|
|
|
|
0 |
|
4 |
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
Пусть кривая задана в полярных координатах |
|||||||||||||||||||||||||||
непрерывной функцией |
|
|
|
|
|
|
, |
|
|
|
|
. |
В |
уравнениях |
|||||||||||||||||||
связи |
|
|
декартовых и полярных |
|
|
|
координат |
x |
cos |
и |
|||||||||||||||||||||||
y |
|
|
|
|
sin формально можно принять параметром |
полярный |
|||||||||||||||||||||||||||
угол |
|
|
, тогда кривую оказывается возможным задать |
||||||||||||||||||||||||||||||
параметрически |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
cos |
, |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
sin . |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Вычисляя |
|
|
производные x |
|
|
|
|
|
|
cos |
|
|
sin |
, |
|||||||||||||
y |
|
|
|
|
|
|
sin |
|
|
|
cos |
|
|
, имеем |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
t |
2 |
y t 2 |
|
|
|
cos |
|
|
|
sin |
2 |
|
sin |
|
cos |
2 |
|
|
|||||||||||




 2
2 

 2 .
2 .
Используя полученный результат, находим формулу для вычисления длины дуги, заданной в полярных координатах:
L |
2 |
2 d . |
|
Пример 9.6. Вычислить длину кардиоиды |
1 sin . |
||
Решение: Кардиоида имеет вид, представленный на рис.
38.
172
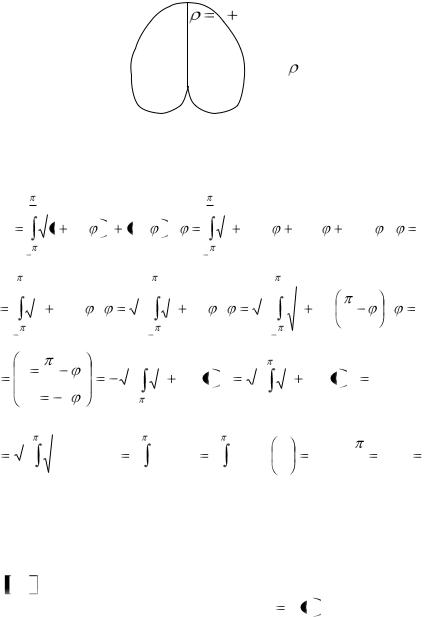
1 sin
O
Рис.38.
Кардиоида имеет две симметричные части. Вычислим длину правой половины кривой:
L |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 sin |
|
|
cos |
|
|
|
|
|
1 |
2sin |
|
|
|
|
|
sin2 |
|
cos2 |
|
d |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
2sin |
|
d |
|
|
2 |
|
1 |
|
sin |
|
|
d |
|
|
|
2 |
|
1 |
cos |
|
|
|
|
|
d |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
|
|
, |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
cos t dt |
|
2 |
|
|
1 |
|
cos t dt |
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dt |
|
|
|
d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
t |
|
|
|
||||||
|
2 |
|
|
|
|
|
2 cos |
|
dt |
2 |
|
cos |
dt |
|
4 cos |
|
d |
|
4sin |
|
4, L 8. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
|
2 |
0 |
||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
9.5. Вычисление объема тела
Пусть требуется найти объем тела, ограниченного замкнутой поверхностью, которое проектируется на отрезок a, b оси Ox , причем известна зависимость площади
поперечного |
сечения |
тела |
S S x |
плоскостью, |
|
|
173 |
|
|

перпендикулярной оси Ox . Предполагается, что S |
S x |
является непрерывной функцией x на отрезке a, b . |
|
Используем метод дифференциала. Через произвольную |
|
точку x проведем плоскость , перпендикулярную оси |
Ox . |
Площадь поперечного сечения равна S x . Через точку x |
dx |
проведѐм другую плоскость, параллельную первой. Тогда из объѐма тела будет выделен «элементарный слой» dV , соответствующий приращению объема. Объем «элементарного слоя» приближенно может быть посчитан как объем цилиндра с основанием S x и высотой dx : dV S(x)dx.
Искомую величину объема находим интегрированием dV в пределах от a до b
|
b |
|
|
|
|
|
V |
S(x)dx . |
|
|
|
|
|
|
a |
|
|
|
|
|
Пример.9.7. Найти объем эллипсоида |
x2 |
|
y 2 |
z 2 1. |
||
4 |
9 |
|||||
|
|
|
||||
Решение: Рассекая эллипсоид плоскостью, параллельной координатной плоскости Oyz и пересекающей ось Ox в точке
x , получим в сечении эллипс
|
|
|
|
|
y 2 |
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
1. |
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
1 |
|
x2 |
|
|
|
|
1 |
|
x2 |
|
|
|
|
|||||||||
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Площадь эллипса равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
S x |
3 1 |
|
|
x 2 |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя зависимость S x , вычислим объем |
||||||||||||||||||||||||
|
2 |
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V |
3 1 |
|
dx 3 x |
|
|
|
8 . |
|||||||||||||||||
|
4 |
12 |
|
|
|
2 |
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление |
|
объема |
|
|
тела |
|
|
вращения |
(рис.39), |
|||||||||||||||
образованного вращением |
вокруг |
|
оси |
|
|
|
|
Ox |
|
криволинейной |
||||||||||||||
|
|
|
|
|
|
|
174 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

трапеции, представляет собой частный случай предыдущей задачи. Пусть криволинейная трапеция, ограниченная сверху непрерывной кривой y  f x , прямыми линиями x a , x b и ось Ox . Любое сечение данного тела плоскостью,
f x , прямыми линиями x a , x b и ось Ox . Любое сечение данного тела плоскостью,
перпендикулярной оси |
Ox , есть круг радиуса R y f (x) . |
|
Поэтому площадь поперечного сечения равна |
|
|
S(x) y 2 |
f (x) 2 и dV |
f (x) 2 dx . |
Объем тела вращения равен |
|
|
b
V  f (x) 2 dx .
f (x) 2 dx .
|
a |
y |
y f x |
O |
a |
x |
b |
x |
Рис.39.
Пример.9.8. Найти объем тела, образованного
вращением |
вокруг оси |
Ox |
фигуры, |
ограниченной линиями |
||||
y x3 , x |
1, y 0 . |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
Объѐм тела вращения равен |
|
|
|
|||||
|
|
1 |
|
|
|
1 |
|
|
|
V |
x6 dx |
|
|
x7 |
|
. |
|
|
7 |
0 |
7 |
|||||
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
175

9.6. Вычисление площади поверхности вращения
|
Пусть кривая |
AB |
является |
графиком функции |
||
y |
f (x) |
0 , заданной на отрезке a, b |
и непрерывной вместе |
|||
с |
ее производной |
y x . |
Найдѐм |
площадь |
поверхности |
|
вращения, |
образованной вращением кривой AB |
вокруг оси |
||||
Ox .
Для вывода формулы площади поверхности вращения используем метод дифференциала. Через произвольную
внутреннюю точку x |
a,b |
проведем перпендикулярную оси |
||||||
Ox плоскость . |
|
|
|
|
|
|||
Плоскость |
пересекает |
поверхность по |
окружности |
|||||
радиуса |
y f |
x |
. Величина |
S |
части поверхности вращения, |
|||
расположенная |
|
левее |
плоскости |
, является функцией x . |
||||
Пусть |
через |
точку |
x dx |
проведена другая |
плоскость, |
|||
параллельная плоскости . Тогда две параллельные плоскости выделят бесконечно узкую полосу поверхности (рис.40), площадь которой dS можно вычислить по формуле площади боковой поверхности усечѐнного конуса, образующая которой
равна dl , а радиусы оснований равны y и y |
dy : |
|||
dS |
y y |
dy |
dl 2 ydl |
dydl . |
y |
y |
f |
x |
|
|
|
|
|
|
O a |
x |
b |
Рис.40.
176

Пренебрегая слагаемым dydl как величиной более высокого порядка малости по сравнению с dl , получаем
dS 2 ydl .
|
|
b |
|
|
Поскольку dl |
1 y x 2 dx , то S 2 y 1 y x 2 dx. . |
|||
|
|
a |
||
Пример.9.9. Найти площадь поверхности шара радиуса
a .
Решение:
Будем считать, что поверхность получена в результате
вращения полуокружности y |
|
|
|
a2 x2 |
|
вокруг оси Ox . |
|||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|||||
S 2 |
|
a2 |
x2 |
1 |
|
|
|
|
|
dx 2 a dx 2 a x |
|
4 a2 . |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
a |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 a |
2 |
x |
2 |
|
|||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если поверхность вращения вокруг оси Ox образована |
|||||||||||||||||||||
кривой, |
|
заданной параметрическими |
уравнениями |
x x t , |
|||||||||||||||||
y y t |
, t1 |
t |
t2 , то площадь поверхности вращения равна |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 2 |
y t |
|
|
|
x t 2 |
|
y t 2 dt. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример.9.10. Найти площадь поверхности, образованной вращением циклоиды вокруг оси Ox .
Решение:
Первая арка циклоиды описывается уравнениями x t sin t,
y 1 cost,
где 0 t 2 . Тогда площадь поверхности вращения равна
2
S 2
0
|
2 |
|
2 |
1 cost |
t sin t |
1 cost |
dt |
177

|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
cost |
|
|
1 |
|
|
cost |
2 |
|
sin t |
|
2 |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
dt = |
|||||||
2 |
|
2 sin |
|
1 |
|
2 cost |
|
|
|
cos |
t |
sin |
t dt |
|
4 |
|
|
sin |
|
2 |
2 cost |
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
t |
|
|
|
|
|
|
2 |
|
t |
|
|
|
|
|
|
2 |
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
t |
|
|
||||||||||
4 |
2 |
|
sin |
|
|
|
|
2 sin |
|
dt |
|
8 |
|
sin |
|
|
sin |
|
dt |
8 |
sin |
|
dt |
|||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|||||
8 |
1 |
|
cos |
2 |
|
|
sin |
|
|
dt |
|
8 |
|
1 |
|
cos |
2 |
|
|
|
d |
|
|
|
2 cos |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
cos |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
64 |
|
|
||||||||||
|
16 cos |
|
|
|
|
|
2 |
|
|
|
|
|
16 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
. |
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
3 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.7. Работа переменной силы |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Работа по перемещению материальной точки |
|
|
|
M вдоль |
||||||||||||||||||||||||||||||||||||||||||||||||||||
оси |
|
Ox |
|
из |
|
|
|
точки |
|
|
|
x |
|
|
|
a |
до |
|
точки |
|
|
|
x |
|
|
|
b |
|
|
под |
действием |
|||||||||||||||||||||||||||
переменной силы F |
|
|
|
F x , направленной по оси Ox , равна |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
b
A  F x dx.
F x dx.
a
Пример.9.11. Найти работу по выкачиванию бассейна с водой, если последний представляет собой куб с ребром a .
Решение:
Используем метод дифференциалов. Введем систему координат как указано на рис. 41.
178

O
a y
x dx
a  x
x
Рис.41.
|
Работа A по выкачиванию слоя жидкости толщиной x |
|||||||||||||||||
0 |
x a |
является функцией x . Найдем дифференциал dA |
||||||||||||||||
как главную часть приращения при изменении x |
на величину |
|||||||||||||||||
x |
dx . Для выкачивания «элементарного слоя» толщиной dx |
|||||||||||||||||
с глубины x требуется затратить |
|
работу |
|
dA |
x dp . |
Здесь |
||||||||||||
dp вес «элементарного слоя», |
равный |
|
g dv , |
где |
g |
|||||||||||||
ускорение |
свободного |
падения, |
|
|
удельный |
вес |
воды, |
|||||||||||
dv |
a2 dx |
|
объем |
«элементарного слоя». |
|
Поскольку |
||||||||||||
dA |
xg a2 dx , |
то, |
интегрируя дифференциал в пределах от 0 |
|||||||||||||||
до a , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
x 2 |
|
|
a |
|
|
|
a 2 |
|
|
ga4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
A |
ga2 |
xdx ga2 |
|
ga |
2 |
|
|
. |
||||||||
|
|
2 |
|
|
0 |
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы для самопроверки
1.Опишите метод интегральных сумм и метод дифференциала.
2.Напишите формулу для вычисления площади плоской фигуры в декартовых координатах.
179

3.Получите формулу площади плоской фигуры, ограниченной линией, заданной параметрическим образом.
4.Площади фигур какого типа вычисляются в полярных координатах?
5.Используя метод интегральных сумм, выведите формулу длины дуги в декартовых координатах.
6.Как выводится формула длины дуги в полярных координатах на основе формулы длины дуги параметрически задаваемой кривой?
7.Как находится объем тела по известной зависимости площади поперечного сечения?
8.Выведите формулу объема тела вращения.
9.Используя метод дифференциалов, получите формулу площади поверхности вращения.
10.Как вычисляется работа по перемещению тела переменной силой?
Задачи для самостоятельного решения
Найти площадь фигуры, ограниченной линиями:
1. |
y2 |
9x, |
y |
3x |
(Ответ: |
|
1 |
). |
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
y |
x2 , |
y |
2 |
x2 (Ответ: |
8 |
). |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3. |
xy |
4, |
x |
4, |
y |
4, x |
0, |
y |
0 (Ответ: 4 ln 4e ). |
||||||||||||
4. |
y |
1 |
x2 , |
y |
2 |
x2 , |
x |
|
|
0, x |
1 |
(Ответ: |
5 |
). |
|||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
5. |
x |
t |
sin t, |
0 |
t |
2 |
|
, осью Ox (Ответ: 3 ). |
|||||||||||||
y |
1 |
cost, |
|
||||||||||||||||||
6. |
x |
cos3 t, |
0 |
t 2 |
|
(Ответ: |
3 |
|
|
). |
|
|
|
||||||||
|
sin3 t, |
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
||||||
7. |
|
1 |
cos |
|
0 |
|
2 |
|
|
(Ответ: |
|
3 |
). |
|
|
||||||
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
180
