Методическое пособие 813

Рис. 8. Зависимость температурного градиента ∆Tгр от амплитуды колебания температуры воздуха

Выводы. Анализ результатов моделирования позволил сделать следующие выводы:

–изменение температурных полей на глубине до 40 см от поверхности аэродромного покрытия в течение 24-часового цикла происходит по гармоническому закону, аналогично температуре окружающего воздуха;

–в границах искусственного покрытия изменение температуры по глубине носит экспоненциальный характер, ниже границы покрытия изменение температуры носит линейный характер;

–увеличение толщины слоя усиления позволяет обеспечить прохождение границы нулевых колебаний в теле конструкции верхнего слоя аэродромного покрытия;

–определив распределение температуры в толще многослойного аэродромного покрытия, становится возможным получить деформационные поля.

91

Научный вестник Воронежского ГАСУ. Строительство и архитектура

Библиографический список

1.Жесткие покрытия аэродромов и автомобильных дорог / Г. И. Глушков [и др.]. — 2-е изд., перераб. и доп. — М.: Транспорт, 1994. — 349 с.

2.Сиденко, В. М. Тепломассообмен в земляном полотне дороги / В. М. Сиденко, С. А. Гриднев // Известия вузов. Строительство и архитектура. — 1966. — Вып. 12. — С. 131—136.

3.Лыков, А. В. Теория теплопроводности / А. В. Лыков. — М.: Высш. шк., 1967. — 600 с.

4.Лыков, А. В. Тепломассообмен: справочник / А. В. Лыков. — М.: Энергия, 1978. — 479 с.

5.Малышев, А. А. Оценка влияния климатических факторов на изменение состояния нежёстких дорожных одежд по прочности: дис…. канд. техн. наук / А. А. Малышев. — Омск, 1986. — 226 с.

6.Hartl, G. Zur Frage der Langsdruckkrafte in Betonfahrbahndecktn / G. Hartl // Strasse und Autobahn. — 1985. — № 5. — P. 200—204.

References

1.Zhestkie pokrytiya ae'rodromov i avtomobil'nyx dorog / G. I. Glushkov [i dr.]. — 2-e izd., pererab. i dop. — M.: Transport, 1994. — 349 s.

2.Sidenko, V. M. Teplomassoobmen v zemlyanom polotne dorogi / V. M. Sidenko, S. A. Gridnev // Izvestiya vuzov. Stroitel'stvo i arxitektura. — 1966. — Vyp. 12. — S. 131—136.

3.Lykov, A. V. Teoriya teploprovodnosti / A. V. Lykov. — M.: Vyssh. shk., 1967. — 600 s.

4.Lykov, A. V. Teplomassoobmen: spravochnik / A. V. Lykov. — M.: E'nergiya, 1978. — 479 s.

5.Malyshev, A. A. Ocenka vliyaniya klimaticheskix faktorov na izmenenie sostoyaniya nezhyostkix dorozhnyx odezhd po prochnosti: dis…. kand. texn. nauk / A. A. Malyshev. — Omsk, 1986. — 226 s.

6.Hartl, G. Zur Frage der Langsdruckkrafte in Betonfahrbahndecktn / G. Hartl // Strasse und Autobahn. — 1985. — № 5. — P. 200—204.

MODELLING A TEMPERATURE MODE

OF A MULTILAYER AIRFIELD SURFACING

A. N. Popov, A. A. Xatuncev, A. N. Masalykin

Military Educational and Scientific Center of the Air Force

«N. E. Zhukovsky and Y. A. Gagarin Air Force Academy»(Voronezh) Russia, Voronezh, tel.: +7-919-243-32-17, e-mail: popalnik@mail.ru

A.N. Popov, PhD in Engineering, Assoc. Prof., Head of the Dept. of Engineering and Airfield Support Russia, Voronezh, tel.: +7-919-246-70-03, e-mail: anton. hatun@yandex.ru

A.A. Xatuncev, PhD in Engineering,

Head of the Laboratory of SRC (Combat Application and Support of the AF)

Russia, Voronezh, tel.: +7-908-130-31-71, e-mail: masalykin-alex@mail.ru

A. N. Masalykin, Lecturer of the Dept. of General Military Disciplines

Statement of the problem. Absence of a standard technique of designing of strengthening structures, the uniform approach to defining the character of the distribution of temperature fields and estimation of temperature pressure of asphalt concrete strengthening layer complicates process of acceptance of design solutions. In the article the physical and mathematical model of the formation of a temperature field of a multi-layered air field based on which the finite element model was implemented in the software complex COMSOL is considered.

Results. The experimental factorial model for the definition of the law of the fluctuation of a temperature in a plane of contact of layers on the basis of computing active experiments in COMSOL with use of the obtained finite element model is constructed.

Conclusions. The obtained data can be used in the course of calculations to design asphalt concrete layers for strengthening asembled air field pavings from prestressed ferro-concrete plates PAG.

Keywords: airfield pavements, asphalt concrete strengthening layer, temperature effect, finite element method, modeling.

92

СТРОИТЕЛЬНАЯ МЕХАНИКА

УДК 624.04

НАПРЯЖЕННОЕ СОСТОЯНИЕ И ДЕФОРМАЦИИ ПРЯМОУГОЛЬНОГО ПРОСТРАНСТВЕННОГО СТЕРЖНЕВОГО ПОКРЫТИЯ

М. Н. Кирсанов

Национальный исследовательский университет «МЭИ» Россия, г. Москва, тел.: (495)362-73-14, e-mail: c216@Ya.ru

М. Н. Кирсанов, д-р физ.-мат. наук, проф.

Постановка задачи. Рассматривается схема упругой пространственной статически определимой фермы регулярного типа с произвольным числом ячеек по сторонам, моделирующая прямоугольное в плане покрытие. Ферма симметричная, размер ячеек в каждом из направлений постоянен. Ферма имеет семь внешних связей — сферический шарнир, цилиндрический и два вертикальных стержня, расположенных в углах конструкции. На ферму действует равномерно распределенная по узлам нижнего пояса нагрузка. Разыскивается аналитическое решение для усилий в стержнях и прогиб фермы.

Результаты. С помощью формулы Максвелла-Мора получена аналитическая зависимость прогиба центра фермы от размеров фермы и чисел шарниров по боковым ее сторонам. Искомая закономерность определялась средствами системы компьютерной математики Maple с помощью решения задачи рекурсии по двум параметрам.

Выводы. Обнаружен минимум в зависимости прогиба от числа панелей, позволяющий оптимизировать размеры конструкции. Найдена асимптотика прогиба по числу панелей.

Ключевые слова: пространственная ферма, покрытие, прогиб, предельные свойства, аналитическое решение.

Введение. Число схем статически определимых ферм ограничено. Поиск новых конструкций представляет отдельную задачу [1, 2]. В настоящей работе исследуется прямоугольная в плане пространственная ферма с плоской гранью [3, 4].

Пространственная статически определимая ферма, как правило, представляет собой твердое тело с шестью степенями свободы и соответственно с шестью стержневыми связями, которые могут моделировать сферический или цилиндрический шарнир. Для таких систем, имеющих прямоугольную в плане форму, в силу того, что три точки определяют плоскость, статически недопустимы четыре вертикальных опорных стержня по углам.

Предлагаемая схема прямоугольной стержневой плиты является редким исключением. Здесь по всем четырем углам фермы располагаются вертикальные опоры, а сама ферма (без опор) представляет собой механизм с одной степенью свободы. Всего же опорных стержней семь. Ферма является регулярной конструкцией с двумя независимыми параметрами, равными числу ячеек по боковым сторонам фермы. Регулярность фермы позволяет получить в аналитической форме решение о напряженном и деформированном состоянии методом индукции, пользуясь методикой, развитой в [3—5], с применением современной системы символьной математики Maple [5].

Результаты, полученные методом индукции, не имеют ограничения на число элементов по точности и времени счета и позволяют получать достаточно компактные формулы для уси-

© Кирсанов М. Н., 2016

93

Научный вестник Воронежского ГАСУ. Строительство и архитектура

лий в стержнях и прогибов. Аналитическое решение может быть как частью решения о статически неопределимой системе методом сил (как расчет основной системы), так и иметь самостоятельное значение, в том числе как тестовое решение.

1. Схема фермы. Ферма представляет собой пространственную статически определимую конструкцию из двух параллельно расположенных стержневых контуров и четырехгранных пирамидальных куполов над нижним контуром (рис. 1—3). Соединения стрежней шарнирные. Нижний контур — это прямоугольная решетка с панелями (ячейками) размером a×b. По оси x пояс содержит n ячеек со стороной a, вдоль оси y — m ячеек размером b. Всего в этом контуре N = nm ячеек. Над каждой ячейкой надстроена пирамида высотой h из четырех одинаковых стержней. Вершины пирамид вдоль боковых сторон конструкции соединяют стержни верхнего контура. Вершины внутренних пирамид не соединены между собой.

Рис. 1. Ферма. Общий вид

В нижнем контуре K (n 1)(m 1) шарнирных узлов и 2N n m стержней, в верхнем — nm узлов и 2(m n 2) стержней. С учетом 4N стержней пирамид в ферме содер-

жится ns 6N 3(n m) 4 стержней и nu N K шарниров. Вместе с семью опорными

стержнями число неизвестных усилий в стержнях конструкции совпадает с числом уравнений равновесий узлов в проекции на три координатные оси:

Система статически определима. Заметим, что в конструкции четыре вертикальных опоры, поддерживающих плоскость нижнего контура. Одна из опор на первый взгляд лишняя, так как плоскость определяют три точки. Но противоречий здесь нет — один опорный стержень взят из самой фермы. Конструкция без указанных семи опорных стержней, составляющих четыре угловые опоры (на рис. 1 опоры указаны без особенностей закрепления), твердым (неизменяемым) телом не является. Только совместно с опорными стержнями задача получается корректно поставленной, что подтверждается тождеством (1). Аналитический расчет прогиба центрального узла подобных ферм от действия одной сосредоточенной силы произведен в [3, 4].

94

Рис. 2. n 4, m 6

Рис. 3. Вид сбоку, n 4

Рис. 4. Ферма в плане, n 4, m 6

95

Научный вестник Воронежского ГАСУ. Строительство и архитектура

Расчет усилий будем производить методом вырезания узлов, составляя уравнения равновесия в проекциях. Направляющие косинусы усилий определим по координатам концов стержней. Для этого введем систему координат с осями x и y вдоль сторон горизонтального покрытия и вертикальной осью z. Начало координат поместим в сферической опоре. В нижнем контуре расположены узлы с координатами

rk [xk , yk ,zk ] [(i 1)a, ( j 1)b, 0],

k i (j 1)(n 1), i 1,...,n 1, j 1,...,m 1.

Координаты узлов верхнего пояса (вершины пирамид):

rk [(i 1/ 2)a, (j 1/2)b, h],

k i (j 1)n K, i 1,...,n, j 1,...,m.

Сферическая опора моделируется тремя стержнями, прикрепленными к узлу 1. Координаты концов этих стержней, закрепленных на земле, имеют вид

rk 3 [x1 1,y1,z1], k N K.

Цилиндрический шарнир моделируется двумя жесткими стержнями, закрепленными в узле с номером n 1. Координаты их концов на основании следующие:

rk 4 [xn 1,yn 1,zn 1 1],

rk 5 [xn 1,yn 1 1,zn 1], k N K.

Две отдельные стойки по другим углам конструкции (узлы K n и K (рис. 4)) имеют следующие координаты концов, закрепленные на основании:

rk 6 [xK n,yK n,zK n 1],

rk 7 [xK ,yK ,zK 1], k N K.

Структура конструкции задается также порядком соединения стержней и узлов. Для этого каждый из ns стержней представляется условным вектором qi , i 1,...,ns , координаты

которого — номера узлов, к которым он присоединен. С точки зрения теории графов [6] такой способ соответствует заданию списка ребер графа. В данном случае для вычисления направляющих косинусов усилий, входящих в уравнения равновесия, такое описание предпочтительней. Очевидно, выбранные направления стержней-векторов не влияют на усилия и знаки усилий в стержнях. Векторы стержней куполов, опирающихся на нижний контур, имеют вид

k i ( j 1)n, i 1,...,n, j 1,...,m.

Продольные стержни решетки нижнего контура заданы векторами:

поперечные стержни:

qk 5N [k n,k 1], k i j(n 1) 1, i 1,...,n 1, j 1,...,m.

96

Выпуск № 1 (41), 2016 ISSN 2072-0041

Верхний контур, соединяющий вершины крайних пирамид и составляющий боковой периметр конструкции, соответствует следующим векторам стержней:

Семь опорных стержней кодируются следующими векторами:

2. Расчет усилий. Алгоритм составления системы уравнений метода вырезания узлов основан на вычислении направляющих косинусов усилий, вычисляемых по заданным координатам, и организации их записи в матрицуG. Уравнения равновесия сводятся к системе

n 2n0 . При этом в ферме существует геометрически центральный узел решетки нижнего

контура, к которому можно приложить вертикальную (вдоль оси z ) единичную нагрузку и по формуле Максвелла-Мора найти прогиб фермы в этом узле (рис. 1). Значение нагрузки присваивается соответствующей компоненте вектора R в правой части системы (2). Цен-

нений равновесия потребуются проекции стержней-векторов на оси координат, которые вычисляем по разности координат шарниров по концам стержня:

номер проекции (на оси x, y, z). Для решения системы линейных уравнений (2) в символьном виде применим операцию вычисления обратной матрицы, имеющую в системе Maple про-

97

Научный вестник Воронежского ГАСУ. Строительство и архитектура

стой вид G 1 1/G. С ее помощью решение системы получается умножением матрицы на вектор нагрузок SP G 1RP , S1 G 1R1 , где SP, S1 — векторы усилий от действия нагрузки и

единичной вертикальной силы, приложенной к центру конструкции. Этот простой прием не требует вызова специализированного пакета LinearAlgebra и сокращает время преобразований. Кроме того, для пересчета результатов на другую нагрузку нет необходимости повторного обращения матрицы, что сокращает время преобразований.

Результатом работы программы являются аналитические выражения для усилий в стержнях фермы. Для вычисления прогиба узла, к которому приложена нагрузка, воспользуемся формулой Максвелла-Мора:

где E — модуль упругости стержней; γF, F — площади сечения стержней куполов и стержней поясов соответственно; γ — безразмерный параметр, характеризующий соотношение сечений стержней куполов и горизонтальных поясов; lj — длина j-го стержня; SP,j — усилия в j- м стержне от действия нагрузки; S1,j — усилие от единичной вертикальной силы, приложенной к центру конструкции. Суммирование ведется по всем стержням фермы, кроме опорных, которые предполагаются жесткими: j = 1, …, ns.

Введем обозначения EF / Psum , где Psum — общая нагрузка на все K (n 1)(m 1) узлы нижнего пояса фермы (включая опоры), а нагрузка на каждый узел P Psum / K . Мето-

дом индукции получим относительный прогиб верхнего узла фермы:

где c a2 b2 4h2 — длина стержней куполов;

An,m n(5n3(m 3) 24n2 4(7m 3)n 24(m 1))/48;

Bn,m Am,n ; Cn,m ((m2 2m 2)n2 2m(m 4)n 2(m2 4))/8.

Коэффициенты An,m, Bn,m и Cn,m получены в два приема. Сначала при фиксированном m методом индукции по n последовательным расчетом в символьной форме в системе Maple получались коэффициенты An,1, An,2, … и Cn,1, Cn,2, …, затем находились общие члены полученных последовательностей. Применялись специальные операторы Maple rgf_findrecur и rsolve. При этом для нахождения коэффициента Bn,m использовалось очевидное условие симметрии формул по переменным a, b и m, n.

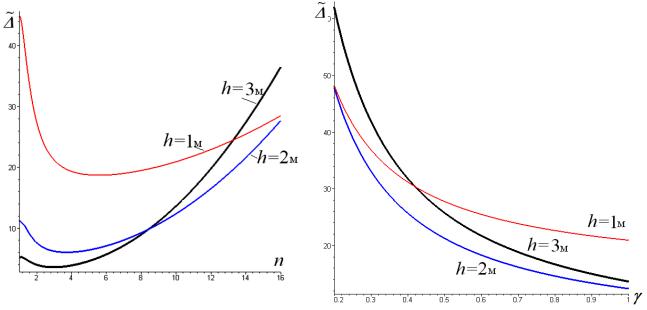
3. Анализ. Полученный результат (4) для прогиба фермы, с одной стороны, в силу достаточной его общности применим для практических расчетов реальных конструкций. С другой стороны, учитывая тот факт, что на практике чаще применяются статически неопределимые конструкции, полученные, например, добавлением к рассмотренной ферме стержней верхнего пояса, соединяющих все вершины пирамид, это решение может быть и простой оценкой прогиба, и частью решения задачи (расчет основной системы) о статически неопределимой ферме методом сил. Кроме того, замкнутая аналитическая форма результата позволяет легко выделить какие-то характерные черты конструкции. Если построить графики зависимости прогиба квадратной в плане фермы с одинаковым числом панелей по сторонам и фиксированной длиной стороны (m = n, a = b = L/n) от числа панелей (рис. 5), то можно заметить, что на кривых имеется минимум. Пересечение кривых, построенных при различных высотах куполов, показывает, что при некоторых значениях n ферма имеет одинаковую же-

98

сткость. При n < 9 расположение кривых вполне логично: чем больше высота куполов, тем меньше прогиб, затем с увеличением числа панелей (при той же суммарной нагрузке и тех же размерах в плане) картина меняется: кривая, соответствующая h = 3 м, оказывается между кривыми h = 1 м и h = 2 м, а при n > 13 ферма с такой высотой становится наиболее гибкой.

Зависимость прогиба от параметра перераспределения площадей сечения γ при фиксированном значении n = 10 (рис. 6) также имеет сходные эффекты. Пересечение кривых при γ = 0,2 и γ = 0,43 указывает на неоднозначность решения, характерную для нелинейного решения (4). Кроме того, аналитическая зависимость (4) дает возможность провести асимптотическое исследование конструкции, получив информацию, недоступную для численных методов. Одной из полезных характеристик конструкции является предельное отношение прогиба к степени числа панелей [7]. Отношение вычисляется при фиксированном пролете и суммарной нагрузке. Оператор limit системы Maple дает следующий результат:

lim / n2 h/(16 ),

n

что согласуется с общим характером кривых на рис. 5, обнаруживающих один минимум. Выводы. Найдено аналитическое выражение для прогиба пространственной статически

определимой фермы под действием равномерно распределенной по узлам нижнего пояса конструкции. Параметрами решения являются размеры фермы, нагрузка и число панелей по ее сторонам. Замкнутая компактная форма аналитического решения позволяет проанализировать его особенности, в частности выяснить характер роста прогиба при увеличении числа панелей фермы при ее постоянных размерах. Было получено, что эта зависимость квадратичная.

Опыт индуктивного получения решения для усилий в стержнях и прогиба показал, что с ростом числа панелей резко увеличивается время символьных преобразований, в то время как скорость численных расчетов почти не меняется. Именно поэтому проверку аналитического решения удобно выполнять численно, задавая все исходные данные в вещественной форме. Однако численные методы могут давать присущие им погрешности округления, мало заметные для небольших ферм и существенные при n > 100—200 в силу того, что размер матрицы системы уравнений равновесия, согласно (1), растет в квадратичной зависимости от n. Одно из назначений точных решений — преодоление «проклятия размерности».

99

Научный вестник Воронежского ГАСУ. Строительство и архитектура

Библиографический список

1.Hutchinson, R. G. Microarchitectured Cellular Solids — the Hunt for Statically Determinate Periodic Trusses / R. G. Hutchinson, N. A. Fleck // ZAMM Z. Angew. Math. Mech. — 2005. — Vol. 85, № 9. — P. 607 — 617.

2.Hutchinson, R. G. The Structural Performance of the Periodic Truss / R. G. Hutchinson, N. A. Fleck // Journal of the Mechanics and Physics of Solids. — 2006. — Vol. 54, № 4. — P. 756—782.

3.Кирсанов, М. Н. Аналитический расчет пространственной стержневой регулярной структуры с плоской гранью / М. Н. Кирсанов // Строительная механика и расчет сооружений. — 2015. — № 2 (259). — С. 2—6.

6.Кирсанов, М. Н. Графы в Maple / М. Н. Кирсанов. — М.: Физматлит, 2007. — 168 с.

7.Тиньков, Д. В. Сравнительный анализ аналитических решений задачи о прогибе ферменных конструкций / Д. В. Тиньков // Инженерно-строительный журнал. — 2015. — № 5 (57). — С. 66—73.

References

1.Hutchinson, R. G. Microarchitectured Cellular Solids — the Hunt for Statically Determinate Periodic Trusses / R. G. Hutchinson, N. A. Fleck // ZAMM Z. Angew. Math. Mech. — 2005. — Vol. 85, № 9. — P. 607 — 617.

2.Hutchinson, R. G. The Structural Performance of the Periodic Truss / R. G. Hutchinson, N. A. Fleck // Journal of the Mechanics and Physics of Solids. — 2006. — Vol. 54, № 4. — P. 756—782.

3.Kirsanov, M. N. Analiticheskij raschet prostranstvennoj sterzhnevoj regulyarnoj struktury s ploskoj gran'yu / M. N. Kirsanov // Stroitel'naya mexanika i raschet sooruzhenij. — 2015. — № 2 (259). — S. 2—6.

4.Kirsanov, M. N. Analiz progiba fermy pryamougol'nogo prostranstvennogo pokrytiya / M. N. Kirsanov // Inzhenerno-stroitel'nyj zhurnal. — 2015. — № 1 (53). — S. 32—38.

5.Kirsanov, M. N. Maple i Maplet. Reshenie zadach mexaniki / M. N. Kirsanov. — SPb: Lan', 2012. — 512 c.

6.Kirsanov, M. N. Grafy v Maple / M. N. Kirsanov. — M.: Fizmatlit, 2007. — 168 s.

7. Tin'kov, D. V. Sravnitel'nyj analiz analiticheskix reshenij zadachi o progibe fermennyx konstrukcij / D. V. Tin'kov // Inzhenerno-stroitel'nyj zhurnal. — 2015. — № 5 (57). — S. 66—73.

STRESS STATE AND DEFORMATION

OF A RECTANGULAR SPATIAL ROD COVER

M. N. Kirsanov

National Research University «MPEI»

Russia, Moscow, tel.: (495)362-73-14, e-mail: c216@Ya.ru

M. N. Kirsanov, D. Sc. in Physics and Mathematics, Prof.

Statement of the problem. The scheme is considered staticallydeterminate elastic regular farm type with an arbitrary number of cells on the sides simulating the rectangular surface. The farm is symmetric, the cell size in each direction is constant. The farm has seven external relations — the spherical hinge, and two vertical cylindrical rod located in the corners of the structure. The farm operates uniformly distributed over the nodes of the lower belt load. Wanted Analytics solutions for efforts in the rods and deflection of the farm.

Results. Using the formula of Maxwell-Mohr obtained the analytical dependence of a deflection of center farm from farm size and number of hinges side by side. The desired pattern was determined by means of a computer algebra system Maple, solve the problem using recursion with two parameters.

Conclusions. A minimum was found in the dependence of the deflection on the number of panels to optimize the size of the structure. The asymptotics of the deflection according to the number of panels was identified.

Keywords: spatial farm, surfacing, deflection, limit properties, analytical solution.

100