
Методическое пособие 398
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Линейная алгебра»
для студентов специальности 38.03.05 «Бизнес-информатика», профиль «Электронный бизнес» очной формы обучения
Воронеж 2015
Составители: канд. физ.-мат. наук С.П. Майорова, канд. физ.-мат. наук М.Г. Завгородний
УДК 512 Методические указания к практическим занятиям по
дисциплине «Линейная алгебра» для студентов специальности 38.03.05 «Бизнес-информатика», профиль «Электронный бизнес» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. С.П. Майорова, М.Г. Завгородний. Воронеж,
2015. 54 с.
Методические указания содержат краткие теоретические сведения, примеры решения задач и задания к практическим занятиям по дисциплине «Линейная алгебра».
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Мет_ЛинАл_ПрЗ.pdf.
Библиогр.: 3 назв.
Рецензент канд. техн. наук, доц. Н.А. Ююкин
Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный технический университет», 2015
ВВЕДЕНИЕ
Система университетского образования предполагает рациональное сочетание таких видов учебной деятельности, как лекции, практические занятия, самостоятельная работа студентов, а также контроль полученных знаний.
Лекции представляют собой систематическое, последовательное изложение учебного материала.
Практические занятия позволяют научиться применять теоретические знания, полученные на лекциях, при решении конкретных задач.
Самостоятельная работа студентов способствует глубокому усвоению учебного материала и развитию навыков самообразования.
Данные методические указания предназначены для студентов специальности 38.03.05 «Бизнес-информатика», профиль «Электронный бизнес» очной формы обучения и имеют своей целью формирование умений и навыков решения практических задач линейной алгебры.
В настоящих методических указаниях содержатся задания к практическим занятиям по темам: определители, матрицы, системы линейных уравнений, линейные пространства.
Тема 1. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ Справочный материал
Определителем второго порядка называется число, ко-
торое вычисляется по формуле:
A |
|
|
a11 |
a12 |
a a |
22 |
a a |
21 |
. |
(1) |
|
||||||||||
|
|
|
a21 |
a22 |
11 |
12 |
|
|
||
|
|
|
|
|
|
|
|
|
Правило. Чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали.
Определителем третьего порядка называется число,
которое вычисляется по формуле:
|
|
a11 |
a12 |
a13 |
|
|
A |
|
a21 |
a22 |
a23 |
a11a22a33 a12 a23a31 a13a21a32 |
|
|
|
a31 |
a32 |
a33 |
|
(2) |
|
|
|
|
a13a22a31 a12 a21a33 a11a23a32.
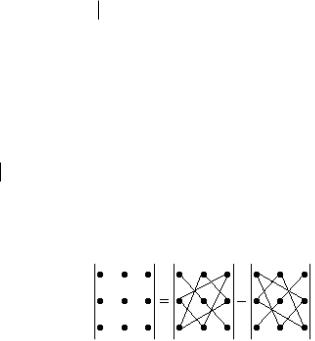
Схематически:
Правило. При вычислении определителей третьего порядка пользуются правилом треугольников:
1)с плюсом берется произведение элементов главной диагонали и элементов, расположенных в вершинах треугольников, одна из сторон которых параллельна главной диагонали;
2)с минусом берется произведение элементов побочной диагонали и элементов, расположенных в вершинах треугольников, одна из сторон которых параллельна побочной диагонали.
2

Свойства определителей
1.При транспонировании определитель не меняется.
2.При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
3.Общий множитель всех элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
4.Если все элементы какой-либо строки (столбца) определителя равны нулю, то определитель равен нулю.
5.Определитель, содержащий две одинаковые строки (столбца), равен нулю.
6.Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
7.Если все элементы какой-либо строки (столбца) определителя представлены в виде суммы двух слагаемых, тогда определитель равен сумме двух определителей, так что:
|
|
|
|
a1 |
b1 |
c1 |
|
|
|
|
|
|
|
|
|||||||||||
a1 a1 |
b1 b1 |
c1 c1 |
|
|
|
a1 |
b1 |
c1 |
|
|||
a2 |
b 2 |
c2 |
|
a2 |
b 2 |
c2 |
|
|
a2 |
b 2 |
c2 |
. |
a3 |
b3 |
c3 |
|
a3 |
b3 |
c3 |
|
|
a3 |
b3 |
c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.Определитель не изменится, если ко всем элементам ка- кой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Для вычисления определителей важным является ещё одно свойство - возможность разлагать определитель по ка- кой-либо строке или столбцу.
Вычеркнем в определителе i -ю строку и j -й столбец, на пересечении которых располагается элемент aij . Получим определитель (n 1) порядка, который называют дополнительным минором элемента aij и обозначают M ij .
Алгебраическим дополнением элемента aij называется
3

число, которое находят по формуле |
|
|
|
A ( 1)i j M |
ij |
. |
(3) |
ij |
|
|
С помощью алгебраических дополнений вычисление определителя n-го порядка можно свести к вычислению определителей меньших порядков.
Теорема (о разложении определителя). Определитель равен сумме произведений всех элементов какой-либо его строки (столбца) на их алгебраические дополнения.
Примеры решения задач
Пример 1. Вычислить определитель |
|
3 |
|
. |
|
|
||||
2 |
|
|
|
|||||||
|
|
|
|
|
5 |
6 |
|
|
|
|
Решение. По формуле (1) получим: |
|
|
|
|
|
|
||||
|
3 |
|
2 6 ( 3) 5 27 . |
|
|
|||||
|
2 |
|
|
|
||||||
|
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
||
Пример 2. Вычислить определитель |
5 |
2 |
1 |
. |
||||||
|
|
|
|
|
1 |
3 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
Решение. Данный определитель вычислим разными способами.
1 способ. Воспользуемся правилом треугольников, т.е. формулой (2):
2 1 3
52 1 2 ( 2) 2 5 ( 3) 3 1 1 1 1 ( 2) 3 5 1 2 1 ( 3) 2
13 2
8 45 1 6 10 6 50.
2 способ. Данный определитель разложим, например, по элементам первого столбца. По теореме о разложении определителя имеем:
4
2 |
1 |
3 |
|
5 |
2 |
1 |
a11A11 a21A21 a31A31 2 A11 5 A21 1 A31 |
1 |
3 |
2 |
|
|
|
|
|
Вычислим алгебраические дополнения элементов первого столбца по формуле (3):
|
11 |
|
2 |
1 |
|
4 |
3 |
1, A |
( 1) |
21 |
|
1 |
3 |
|
(2 |
9) |
11 , |
|||
|
|
|
|
|||||||||||||||||
A ( 1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11 |
|
|
|
3 |
2 |
|
|
|
|
21 |
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
A ( 1)31 |
1 |
|
|
1 6 7 . |
|
|
|
|
|
|
|
|
|
|||||||
31 |
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем значение определителя: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
5 |
2 |
1 |
2 A11 5 A21 1 A31 |
|
|
|
|
|
|||||||||||
|
1 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( 1) 5 ( 11) 1 7 2 55 7 50.
3 способ. Вычисление определителя разложением по элементам какого-либо столбца или строки можно упростить, если в столбце (строке) предварительно получить нули.
Получим нули, например, во втором столбце, а затем разложим определитель по этому столбцу. Для этого первую строку оставим без изменения; ко второй строке добавим первую, умноженную на 2; к третьей строке добавим первую, умноженную на 3. После таких преобразований получим определитель, равный исходному (в силу свойства 8):
|
1 |
3 |
|
2 3 |
|
2 |
1 |
3 |
|
|||
|
2 |
|
|
|
||||||||
|
5 |
2 |
1 |
|
|
| |
|
|
9 |
0 |
7 |
. |
|
1 |
3 |
2 |
|
|
|
|
|
7 |
0 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь определитель можно легко вычислить, используя разложение по второму столбцу:
5
2 |
1 |
3 |
|
|
|
12 |
|
|
9 |
7 |
|
|
|
|
|
|
|
||||||||
9 |
0 |
7 |
|
|
|
|
|
|||||
1 A 0 A 0 A 1 A 1 ( 1) |
|
|
|
|
||||||||
|
|
|
12 |
22 |
32 |
12 |
|
|
7 |
11 |
|
|
7 |
0 |
11 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
(99 49) 50.
Отметим, что при выполнении таких преобразований строка, которая умножается на число, должна оставаться в определителе без изменения.
Пример 3. Вычислить определитель четверого порядка:
|
1 |
0 |
2 |
1 |
|
|
1 |
1 |
0 |
1 |
. |
2 |
0 |
1 |
3 |
|
|
|
0 |
2 |
5 |
2 |
|
|
|
|
|
|
|
Решение. Для разложения определителя удобно взять второй столбец, так как в нем уже имеются два нуля. Получим:
a12 A12 a22 A22 a32 A32 a42 A42 1 A22 2 A42
|
1 |
2 |
1 |
|
1 |
2 |
1 |
|
1 ( 1)22 |
2 |
1 |
3 |
2 ( 1)42 |
1 |
0 |
1 |
5 2 ( 12) 19 . |
|
0 |
5 |
2 |
|
2 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
Пример 4. Вычислить определитель четверого порядка:
|
1 |
0 |
3 |
4 |
|
|
1 |
1 |
2 |
5 |
. |
7 |
2 |
3 |
4 |
|
|
|
0 |
1 |
6 |
8 |
|
|
|
|
|
|
|
Решение. Если данный определитель сразу разложить, например, по первому столбцу, то его вычисление сведется к вычислению трех определителей третьего порядка. Данный способ не является эффективным. Поэтому преобразуем определитель таким образом, чтобы все элементы первого столбца стали равными нулю, кроме одного.
6
Для вычисления данного определителя "сделаем нули", в первом столбце, а затем разложим определитель по этому столбцу. Первую строку определителя оставим без изменения; ко второй строке прибавим первую, умноженную на (- 1); к третьей строке прибавим первую, умноженную на (-7). При таких преобразованиях величина определителя не изменится (в силу свойства 8 определителей). Имеем:
|
0 |
3 |
4 |
|
( 1) ( 7) |
|
1 |
0 |
3 |
4 |
|
|||
|
1 |
|
|
|
||||||||||
|
1 |
1 2 |
5 |
|
|
| |
|
|
0 |
1 |
1 |
1 |
. |
|
|
2 3 |
4 |
|
|
|
|
|
2 |
18 |
32 |
||||
7 |
|
|
|
0 |
|
|||||||||
|
0 |
1 |
6 |
8 |
|
|
|
|
|
0 |
1 |
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложим полученный определитель по первому столбцу:
a11A11 a21A21 a31A31 a41A41 1 A11 0 A21 0 A31 0 A41
|
1 |
1 |
1 |
|
|
|
|||
1 A |
2 |
18 |
32 |
. |
11 |
|
|
|
|
|
1 |
6 |
8 |
|
|
|
|
|
|
Полученный определитель третьего порядка также вычислим с помощью разложения. "Сделаем нули" в первом столбце. Предварительно из второй строки вынесем общий множитель (-2). Затем ко второй строке прибавим первую, и к третьей - прибавим первую. Получим:
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
|
|
|
||||||
( 2) |
1 |
9 |
16 |
( 2) |
0 |
8 |
17 |
. |
|
1 |
6 |
8 |
|
0 |
5 |
9 |
|
|
|
|
|
|
|
|
|
|
Разложим последний определитель по элементам первого столбца; окончательно получим:
1 1 |
8 |
17 |
2 |
(72 |
85) |
26 . |
( 2) ( 1) ( 1) |
5 |
9 |
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
7
Задачи и упражнения для самостоятельного решения
Вычислите определители второго порядка:
1. |
|
|
2 |
|
|
2. |
|
2 |
|
3 |
|
3. |
|
3 2 |
|
4. |
|
3 |
12 |
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
|
6 |
|
|
|
6 |
10 |
|
|
4 |
5 |
|
|
1 |
4 |
|
|||||||
|
|
|
1 |
|
|
|
x 1 |
x 1 |
|
|
|
cos |
sin |
|
|
|
|||||||
5. |
|
a |
6. |
|
|
|
7. |
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
x 1 |
|
sin |
cos |
|
|
|
|||||||||
a |
|
|
a |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислите определители третьего порядка с помощью правила треугольников:
|
5 |
2 |
3 |
|
1 |
4 |
3 |
|
x |
a |
a |
8. |
4 |
3 |
2 |
9. |
3 |
2 |
1 |
10. |
a |
x |
a |
|
2 |
3 |
1 |
|
5 |
6 |
3 |
|
a |
a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
2 |
|
3 |
4 |
5 |
|
1 2 |
1 |
|
|
|
|
|
|
|||||||||
11. |
2 |
8 |
1 |
12. |
8 |
7 |
2 |
13. |
3 |
1 |
5 |
|
|
1 |
1 |
2 |
|
2 |
1 |
8 |
|
4 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислите определители третьего порядка, разложив их по элементам первого столбца:
|
3 |
4 |
|
x |
1 |
x |
|
|
|
2 |
|
|
|||||
14. |
5 |
2 |
1 |
15. |
0 |
x |
1 |
|
|
1 |
2 |
3 |
|
x |
1 |
x |
|
|
|
|
|
|
|
|
|
|
Вычислите определители четвертого порядка:
|
|
0 |
2 |
1 |
|
2 |
1 |
3 |
1 |
|
|
1 |
|
|
|||||||
16. |
1 |
1 |
0 |
1 |
17. |
3 |
2 |
1 |
0 |
|
2 |
0 |
1 |
3 |
1 |
3 |
4 |
2 |
|
||
|
0 |
2 |
5 |
2 |
|
2 |
1 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
8
