
- •Министерство образования и науки Российской Федерации
- •§ 1 Введение в интегралы или подготовка к восприятию интегралов
- •§2 Первообразная функция и неопределённый интеграл
- •11. (1X.)*
- •2. Интегрирование методом разложения подынтегральной функции.
- •3. Метод замены переменной.
- •4. Интегрирование по частям.
- •§4 Интегрирование некоторых классов функци
- •1. Интегрирование рациональных функций
- •2 .Интегрирование тригонометрических функций.
- •3. Интегрирование некоторых иррациональных функций.
- •§5 Интегралы, не выражающиеся через элементарные функции
3. Интегрирование некоторых иррациональных функций.
1.
Интегралы вида
![]() ,
гдеR
– рациональная функция своих аргументов
решаются подстановкой x=tk
k-наименьшее
общее кратное знаменателей дробных
показателей.
,
гдеR
– рациональная функция своих аргументов
решаются подстановкой x=tk
k-наименьшее
общее кратное знаменателей дробных
показателей.
Пример 1. Найти
![]() ,
Решение. Полагаемx=t6,
тогда dx=6t5dt,
,
Решение. Полагаемx=t6,
тогда dx=6t5dt,
![]() t3,
t3,
![]() t2,
получаем
t2,
получаем
![]() =
=![]() =
=![]() =
=![]() =
=
=6![]() =6(t-arctgt)+C= =6(x1/6+arctgx1/6)+C.
=6(t-arctgt)+C= =6(x1/6+arctgx1/6)+C.
2.
Интегралы вида![]() ,
еслиR
рациональная функция своих аргументов,
решаются подстановкой
,
еслиR
рациональная функция своих аргументов,
решаются подстановкой![]() =tk,
где k-наименьшее
общее кратное знаменателей дробных
показателей.
=tk,
где k-наименьшее
общее кратное знаменателей дробных
показателей.
Пример 2. Найти
![]() .
Решение. Полагаемx-1=t4,
тогда dx=4t3dt,
.
Решение. Полагаемx-1=t4,
тогда dx=4t3dt,
![]() =t,
=t,
![]() =t2,получаем
=t2,получаем
![]() =
=![]() .
Последний интеграл является интегралом
от неправильной рациональной дроби.
Выделим целую часть. Отнимем и прибавим
в числителе единицу. Сгруппируем,
почленно разделим, двучлен х4-1
разложим как разность квадратов,
сократив, получим
.
Последний интеграл является интегралом
от неправильной рациональной дроби.
Выделим целую часть. Отнимем и прибавим
в числителе единицу. Сгруппируем,
почленно разделим, двучлен х4-1
разложим как разность квадратов,
сократив, получим
![]() =
=![]() =
=![]() =
=![]() =4(
=4(![]() +t+
+t+![]()
+C
=4/3![]() +2ln|
+2ln|![]() +C.
+C.
3.
Интегралы вида: 1.
![]() ,11.
,11.![]() ,111.
,111.![]() ,
гдеR-рациональная
функция своих аргументов, решаются с
помощью тригонометрических подстановок:
1. x=
,
гдеR-рациональная
функция своих аргументов, решаются с
помощью тригонометрических подстановок:
1. x=![]() ,
11.
,
11.
x=atgt, 111. x=asint, которые приводят к рациональным функциям относительно sint и cost.
Пример 3. Найти
![]() .
Решение. Интеграл111.
вида. Положим
x=sint,
dx=costdt,
.
Решение. Интеграл111.
вида. Положим
x=sint,
dx=costdt,
![]() =cost,
получим
=cost,
получим
![]() =
=![]() =
=![]() =
=
=![]() =
=
![]() (t-
(t-![]() sin2t)+С=
sin2t)+С=![]() (t-sintcost)+C
=
(t-sintcost)+C
=![]() (arcsinx-x
(arcsinx-x![]() )+C.
)+C.
Этот интеграл решён в примере 2 (*) §3 п3. методом интегрирования по частям. Мы ещё раз убедились в том, что путей нахождения интегралов много и в этом плане нахождение интегралов является более интересным, чем дифференцирование функций.
4. Интегралы
вида
![]() выделением под корнем полного квадрата
приводятся к интегралам1.,
11., 111. пункта
3.. Покажем
это на примере.
выделением под корнем полного квадрата
приводятся к интегралам1.,
11., 111. пункта
3.. Покажем
это на примере.
Пример 4. Найти
![]() .
Выделим в подкоренном выражении полный
квадрат. 4x2+4x-15=4(x2+x+1/4-1/4-15/4)=4((x+1/2)2-4).
Выполним замену переменной. Положим
x+1/2=t,
тогда x=t-1/2
, dx=dt,
получим
.
Выделим в подкоренном выражении полный
квадрат. 4x2+4x-15=4(x2+x+1/4-1/4-15/4)=4((x+1/2)2-4).
Выполним замену переменной. Положим
x+1/2=t,
тогда x=t-1/2
, dx=dt,
получим
![]() =
=![]() =
=![]() .
Сделаем новую заменуt=
.
Сделаем новую заменуt=![]() ,
dt=
,
dt=![]() ,
,
![]() =
=![]() 2tgz.
Получим
2tgz.
Получим
![]() =
=![]() =4
=4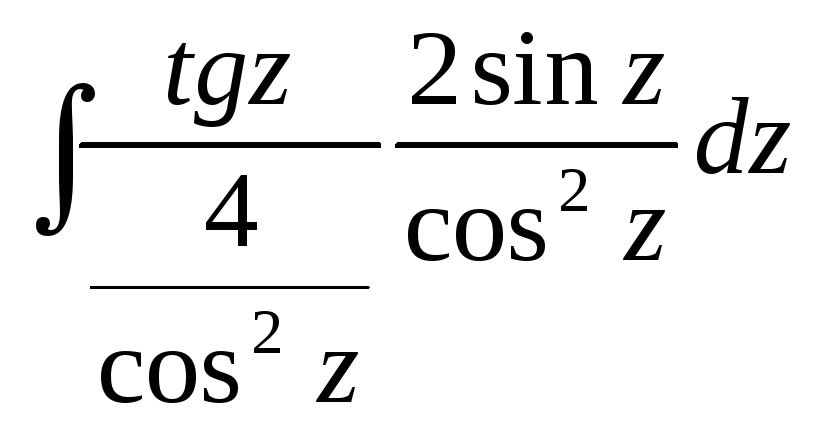 =2
=2![]() =2
=2![]() =
=
=2![]() -2
-2![]() =2
=2![]() -2sinz=2
-2sinz=2![]() -2sinz=2
-2sinz=2![]() -2sinz=
=ln
-2sinz=
=ln![]() -2sinz+C.
(Смотри формулу XV.
таблицы 2)
-2sinz+C.
(Смотри формулу XV.
таблицы 2)
Выполним обратную
замену. Так как t=![]() ,
то cosz=
,
то cosz=![]() ,z=arccos
,z=arccos![]() ,
гдеt=x+1/2.
Получим
,
гдеt=x+1/2.
Получим
![]() =
ln
=
ln![]() -2sinz+C=
ln
-2sinz+C=
ln![]() -2
-2![]() +C=
+C=
=ln![]() +
+![]() +C=ln
+C=ln![]() +
+
+![]() +C.
+C.
§5 Интегралы, не выражающиеся через элементарные функции
Известно, что
всякая непрерывная на [a,
b]
функция f(x)
имеет первообразную, т.е. существует
такая функция F(x),что
F′(x)=f(x).
Однако не всякую первообразную F(x)
можно выразить через элементарные
функции. Так при нахождении интегралов
вида
![]() их первообразные выражаются через
элементарные функции только в трёх
случаях:
их первообразные выражаются через
элементарные функции только в трёх
случаях:
р-целое;
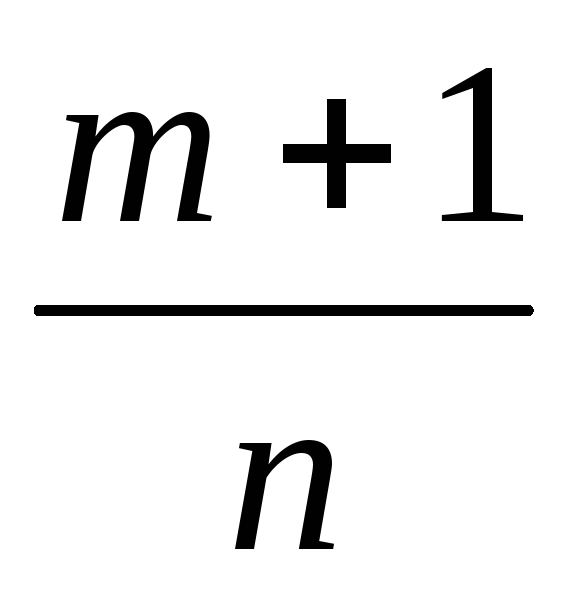 -целое;
-целое;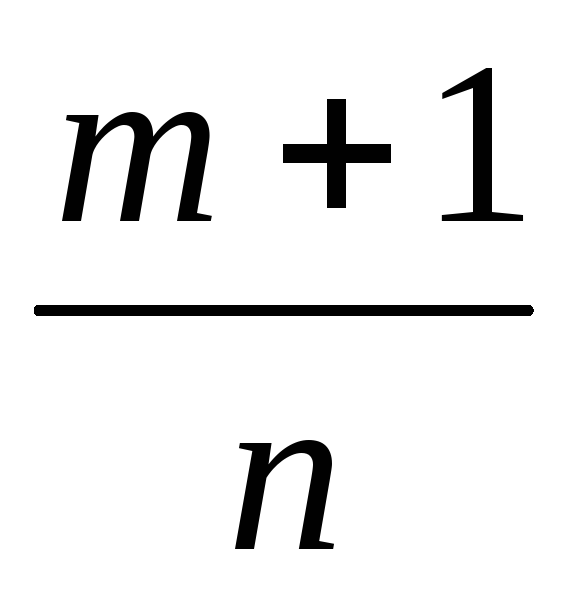 +р
–целое.
+р
–целое.
Во всех остальных случаях данный интеграл не выражается через элементарные функции.
Приведём примеры интегралов, которые не выражаются через элементарные функции, каждый из которых имеет определённое название:
![]() - интеграл Пуассона,
- интеграл Пуассона,
![]() - интегральный
синус,
- интегральный
синус,
![]() - интегральный
косинус,
- интегральный
косинус,
![]() -
интегральный логарифм,
-
интегральный логарифм,
![]() - интегралы
- интегралы
![]() -
Френкеля,
-
Френкеля,
![]() - эллиптический
интеграл первого рода,
- эллиптический
интеграл первого рода,
![]() dx
– эллиптический
интеграл второго рода.
dx
– эллиптический
интеграл второго рода.
С некоторыми из этих интегралов познакомимся позже.
