§ 40. Потік вектора напруженості електричного поля. Теорема Гауса для електричного поля у вакуумі
Експериментально встановлені закон Кулона і принцип суперпозиції дозволяють повністю описати електростатичне поле заданої системи зарядів. Проте, властивості електростатичного поля можна виразити в іншій, загальнішій формі, не удаючись до уявлення про кулонівське поле точкового заряду.
Лінії напруженості електричного поля
Для зручності і наочності електричне поле часто зображують графічно за допомогою силових ліній напруженості. Це лінії, дотичні до яких в кожній точці співпадають з напрямом вектора напруженості.
Лініям напруженості приписують напрям, співпадаючий з напрямом вектора напруженості, вони завжди починаються на позитивному заряді і закінчуються на негативному. Оскільки в кожній цій точці простору вектор напруженості має лише один напрям, то лінії напруженості ніколи не перетинаються. На рисунку 3.6. показані лінії напруженості електричного поля.
Рисунок 3.6.
Силові лінії проводяться в такій кількості, щоб для будь-якої області поля виконувалася наступна чисельна рівність: число силових ліній, що пронизують одиницю площі поверхні, перпендикулярну лініям напруженості, має дорівнювати модулю вектора Е.
Введемо нову фізичну величину, що характеризує електричне поле - потік Φ вектора напруженості електричного поля.
Нехай в просторі, де створено електричне поле, розташований деякий досить малий майданчик ΔS. Добуток модуля вектора Е на площу ΔS і на косинус кута α між вектором Е і нормаллю n до майданчика називається елементарним потоком вектора напруженості через майданчик ΔS (рис. 3.7) :
ΔΦ = EΔS cos α = EnΔS, або dΦ=EndS . (3.6)
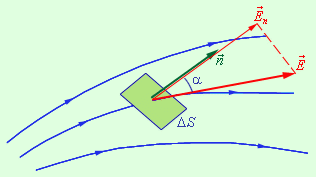
Рисунок 3.7.
Розглянемо тепер деяку довільну замкнуту поверхню S (рис 3.8). Якщо розбити цю поверхню на малі майданчики ΔSi, і визначити елементарні потоки ΔΦi поля E через ці малі майданчики, а потім їх підсумувати, то в результаті ми отримаємо потік Φ вектора E через замкнуту поверхню S:
.
(3.7)
У разі замкнутої поверхні завжди вибирається зовнішня нормаль.
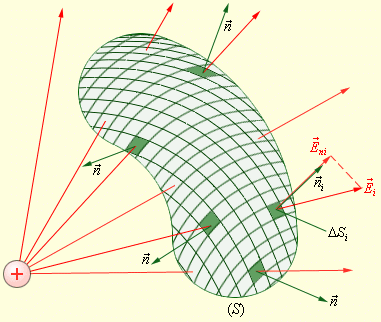
Рисунок 3.8.
Теорема Гауса стверджує:
Потік вектора напруженості електростатичного поля у вакуумі через довільну замкнуту поверхню дорівнює сумі зарядів, розташованих усередині цієї поверхні поділену на електричну сталу ε0.
(3.8)
Використовуючи теорему Гауса, можна у ряді випадків легко розрахувати напруженість електричного поля навколо зарядженого тіла, якщо заданий розподіл зарядів має яку-небудь симетрію.
Знайдемо напруженість поля тонкостінного полого однорідно-зарядженого довгого циліндра радіусу R. З міркувань симетрії, електричне поле має бути спрямоване по радіусу. Тому для застосування теореми Гауса доцільно вибрати замкнуту поверхню S у вигляді співвісного циліндра деякого радіусу r і довжини L, закритого з обох торців (рис 3.9).
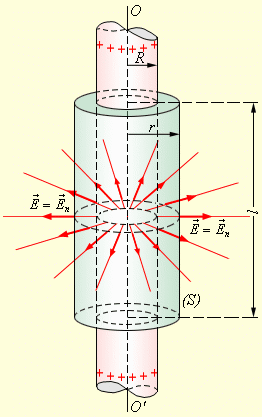
Рисунок 3.9.
При r ≥ R увесь потік вектора напруженості проходитиме через бічну поверхню циліндра, площа якої дорівнює 2πrL, оскільки потік через обидві основи дорівнює нулю. Застосування теореми Гауса дає:
(3.9)
де τ= q/L - лінійна густина заряду.
Цей результат не залежить від радіусу R зарядженого циліндра, тому він може застосовуватися і до поля довгої однорідної зарядженої нитки.
Для визначення напруженості поля усередині зарядженого циліндра треба побудувати замкнуту поверхню для випадку r < R. В даному випадку потік вектора напруженості через бічну поверхню циліндра гауса має бути і в цьому випадку рівний Φ = E2πrL. Згідно з теоремою Гауса, цей потік пропорційний заряду, що виявився усередині замкнутої поверхні. Цей заряд дорівнює нулю. Звідси витікає, що електричне поле усередині однорідно-зарядженого довгого порожнистого циліндра дорівнює нулю.
Аналогічним чином можна застосувати теорему Гауса для визначення електричного поля у ряді інших випадків, коли розподіл зарядів має яку-небудь симетрію. У кожному з таких випадків треба вибирати замкнуту поверхню доцільної форми. Наприклад, у разі центральної симетрії поверхню зручно вибирати у вигляді сфери з центром в точці симетрії. При осьовій симетрії замкнуту поверхню треба вибирати у вигляді співвісного циліндра, замкнутого з обох торців (як в розглянутому вище прикладі). Якщо розподіл зарядів не має якої-небудь симетрії і загальну структуру електричного поля вгадати неможливо, застосування теореми Гауса не може спростити завдання визначення напруженості поля.
Розглянемо ще один приклад симетричного розподілу зарядів - визначення поля рівномірно зарядженої площини (рис. 3.10).
Рисунок 3.10.
В цьому випадку поверхню Гауса S доцільно вибрати у вигляді циліндра деякої довжини, закритого з обох торців. Вісь циліндра спрямована перпендикулярно зарядженій площині, а його торці розташовані на однаковій відстані від неї. Через симетрію поле рівномірно зарядженої площини має бути скрізь спрямоване по нормалі. Застосування теореми Гауса дає:
(3.10)
де σ =q/S - поверхнева густина заряду, тобто заряд, що приходиться на одиницю площі.
Отриманий вираз для електричного поля однорідної зарядженої площини можна застосувати і у разі плоских заряджених площин кінцевого розміру. В цьому випадку відстань від точки, в якій визначається напруженість поля, до зарядженої площини має бути значно менша розмірів площини.