Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Дальневосточный федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект лекций по алгебре

.pdf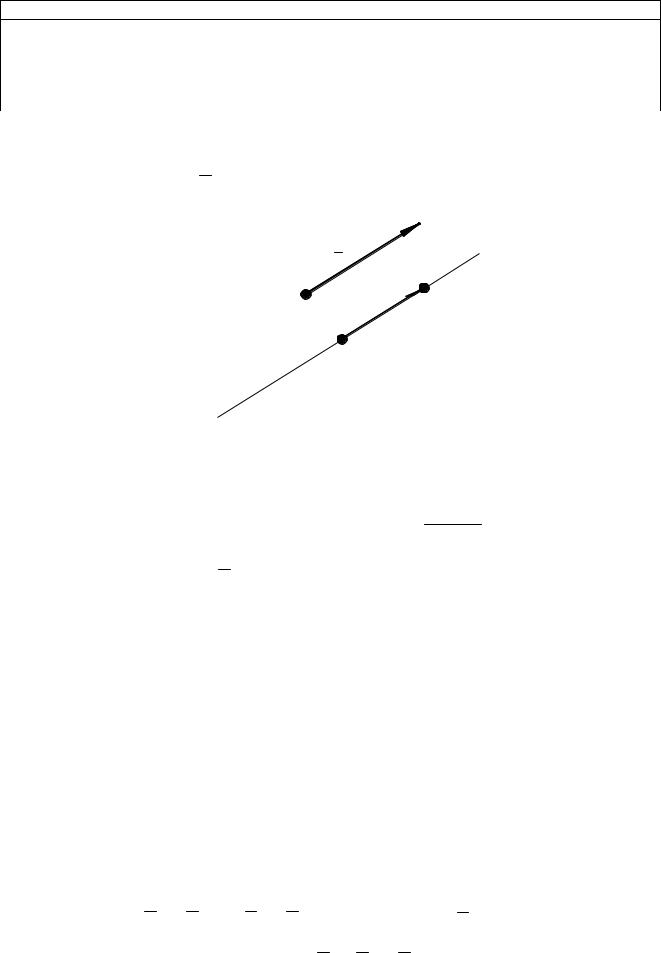

Скачиваний:

Добавлен:

01.05.2015

Размер:

1.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 81 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа

проходящей через заданную точку M0(x0; y0; z0) и имеющей заданный направляющий вектор a (l;m;n).

Рис. 9.2

Возьмем произвольную точку пространства M(x; y; z) лежащую на

прямой M L, построенный на точках вектор M0M будет параллелен направляющему вектору a. В координатной форме это условие запишется:

	x x0		y y0		z z0	(9.2)
	l		m		n

Уравнение принято		называть		каноническим		уравнением прямой в
пространстве.

Задача. Как от уравнения вида (9.1) перейти к уравнению вида (9.2).

Достаточно найти: 1) хотя бы одну точку M0(x0; y0; z0), решая систему уравнений (9.1);

2) т. к. a n1 и a n2, можно найти a, воспользовавшись

свойством векторного произведения: a n1 n2.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:		Идентификационный			Контрольный экземпляр			Лист
		номер:			находится на кафедре			стр. 82 из 172
Дегтярева Н.Е.					Алгебры, геометрии и
					анализа
Уравнение прямой, проходящей через две различные точки
Пусть	даны		две точки в	пространстве:		M1(x1; y1; z1) и
M2(x2; y2; z2).
Произвольная			точка M L		тогда и	только	тогда, когда

M1M || M1M2 (рис. 9.3) (или можно воспользоваться каноническим видом

(9.2)).

Рис. 9.3

Условие коллинеарности векторов в координатной форме дадут уравнение:

x x1	y y1	z z1	(9.3)
x2 x1	y2 y1	z2 z1

- уравнение прямой, проходящей через две точки.

Параметрическое уравнение прямой в пространстве

Возьмем каноническое уравнение прямой и приравняем его к

произвольному параметру t: x x0 y y0 z z0 t.

l m n

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 83 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа

Раскрывая пропорции, получим параметрическое уравнение прямой в пространстве

x x0	l t,
	m t,
y y0	m t,	(9.4)
	n t.
z z0	n t.

Если принять параметр t за время, отсчитываемое от некоторого начального момента, то параметрические уравнения определяют закон движения материальной точки по прямой линии с постоянной скоростью

l2 m2 n2 (такое движение происходит по инерции).

Угол между прямыми в пространстве. Условия параллельности и

перпендикулярности прямых плоскостей и

Пусть даны две прямые, заданные каноническими уравнениями:

L :

x x1

y y1

z z1

(l ; m ; n )- направляющий вектор L ,

L :

x x2

y y2

z z2

; n

)- направляющий вектор L .

Тогда cos

l1 l2 m1

2 n1 n2

l12 m12 n12

l22 m22 n22

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:

Идентификационный

Контрольный экземпляр

Лист

номер:

находится на кафедре

стр. 84 из 172

Дегтярева Н.Е.

Алгебры, геометрии и

анализа

Прямые

l , l

параллельны, если

, то есть

Прямые l1,

ортогональны,

если

2 то

2 0,

l1 l2 m1 m2 n1 n2 0.

Условие принадлежности двух прямых к одной плоскости

Прямые l1,l2 в пространстве могут быть:

1) Параллельными

прямые принадлежащиеоднойплоскости

2)Пересекающимися

3)Скрещивающимися

(две прямые, через которые нельзя провести плоскость)

Для того, чтобы

прямые l1, l2

принадлежали

плоскости ,

необходимо и достаточно, чтобы

a1,

M1M2

были компланарны

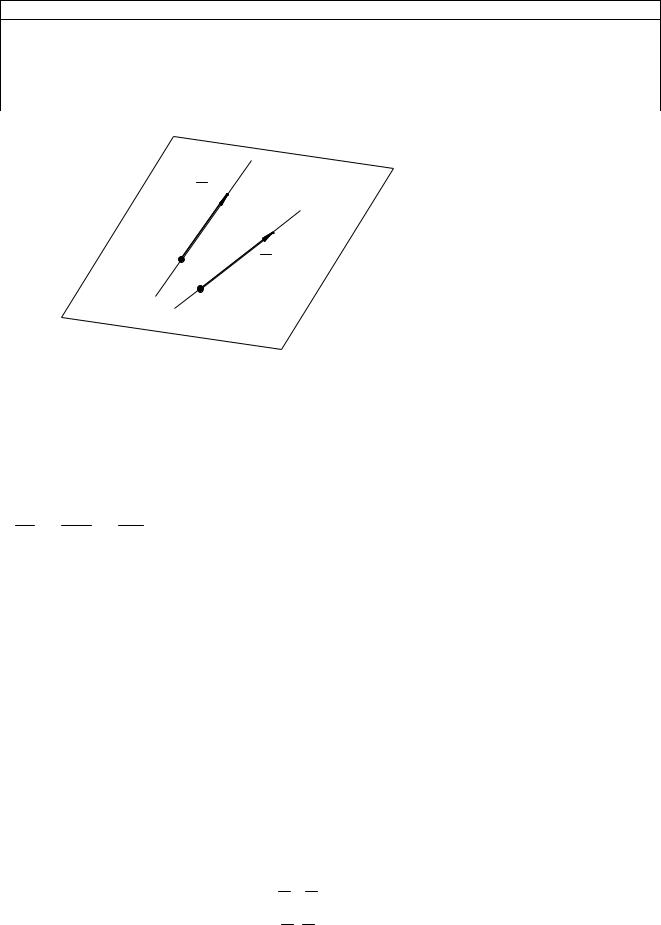
(рис. 9.4) , т. е.

x2 x1

y2 y1

z2 z1

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 85 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа

	l1
	a1
	M1	l2
	M1	a2
		a2
	M2

Рис. 9.4

Чтобы l1, l2 пересекались, должно выполняться еще одно условие, а

именно: их направляющие вектора не должны быть коллинеарными

l1 m1 n1 . l2 m2 n2

Угол между прямой и плоскостью. Условие параллельности и

перпендикулярности прямой и плоскости

Пусть даны		плоскость		: Ax By Cz D 0,			и прямая
l :	x x1	y y1	z z1	(рис 9.5)	–	угол между	прямой l	и
	l	m	n

плоскостью		.	Определим		его	значение.	Т.	к.

90 90 , и cos(90 ) sin . Мы получили,

что угол между прямой и плоскостью можно вычислить по формуле:


sin	a			n	(9.5)
		a	n

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 86 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа

		Рис. 9.5
Подставляя	координаты	векторов	получим	выражение
sin	A l B m C n		.

A2 B2 C2 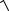l2 m2 n2

Если прямая параллельна плоскости, l || , то n a и следовательно

n a 0 или A l B m C n 0.

Если прямая ортогональна плоскости l α, то n||a и выполняется

пропорция

m n

Для того чтобы прямая l :

x x1

y y1

z z1

принадлежала

плоскости : Ax By Cz D 0

необходимо, чтобы

выполнялись

условия:

1) Ax1 By1 Cz1 D 0,

то есть

M1(x1; y1; z1) ;

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр				Лист
	номер:	находится на кафедре				стр. 87 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа
2) A l B m C n 0		(	n	a	, то есть l \|\| ).

Определение. Совокупность всех прямых, проходящих через данную точку M1(x1; y1; z1), называется связкой прямых (с центром в точке

M1(x1; y1; z1)).

Уравнение

связки прямых:

x x1

y y1

z z1

где

0).

l, m, n (и

l2 m2 n2

Пример. Дано общее уравнение прямой:

x y 2z 4 0

нужно

3x y 5z 8 0

найти каноническое уравнение этой прямой.

(1; 1;2),

(3;1; 5),

Решение.

значит

(3;11;4). Найдем точку, принадлежащую ,

полагая что

z 0

x y 4

4x 4

y 4 1 5,

M0(1;5;0)

следует,

3x y 8

x 1

принадлежит , следовательно,

x 1

y 5

z 0

Некоторые задачи на прямую и плоскость в пространстве.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:		Идентификационный			Контрольный экземпляр			Лист
		номер:			находится на кафедре			стр. 88 из 172
Дегтярева Н.Е.					Алгебры, геометрии и
					анализа
Задача	1.		Найти	условие	пересечения	трех	плоскостей

1 : A1x B1y C1z D1 0

2 : A2x B2y C2z D2 0 в одной и только одной точке.

3 : A3x B3y C3z D3 0

Чтобы три плоскости 1, 2, 3 пересекались в одной точке

необходимо		и		достаточно, чтобы выполнялось условие
	A1	B1	C1
	A1	B1	C1
	A2	B2	C2	0
	A3	B3	C3

Задача 2. Записать уравнение прямой, проходящей через данную точку

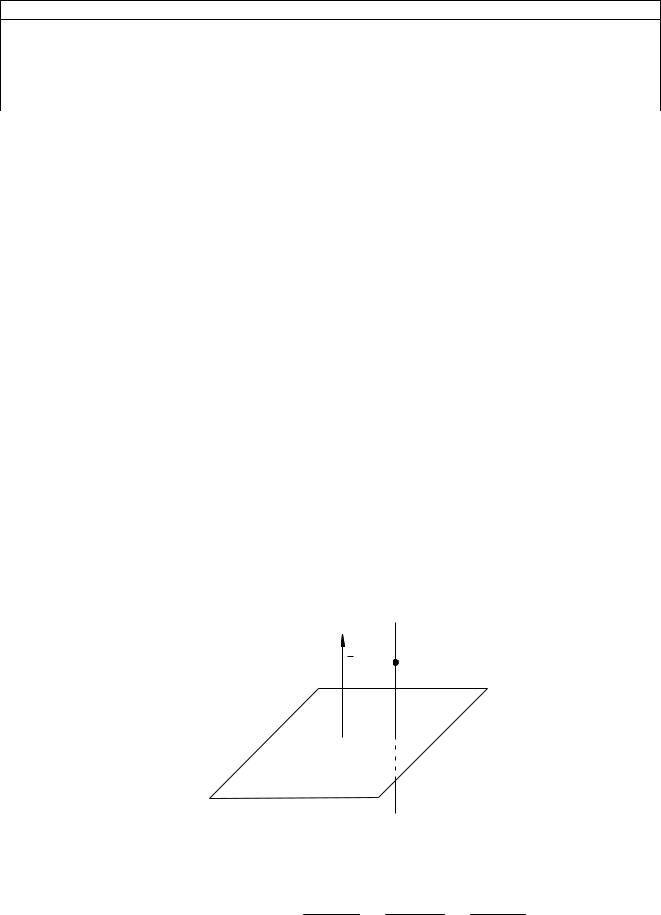
M1(x1; y1; z1) и перпендикулярную данной плоскости

Ax By Cz D 0 (рис. 9.6)

	L
n	M1

Рис. 9.6

Искомая прямая имеет вид l : x x1 y y1 z z1 .

A B C

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 89 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа

Задача 3. Записать уравнение плоскости, проходящей через прямую

l :

x x1

y y1

z z1

и точку M

(x , y

) l(рис. 9.7).

M 0

M1(x1, y1,z1)

Рис. 9.7

1) находим нормальный вектор для нашей плоскости

n M1M0 a ;

2) используя точку M0 и найденный нормальный вектор n,

записываем общее уравнение плоскости ..

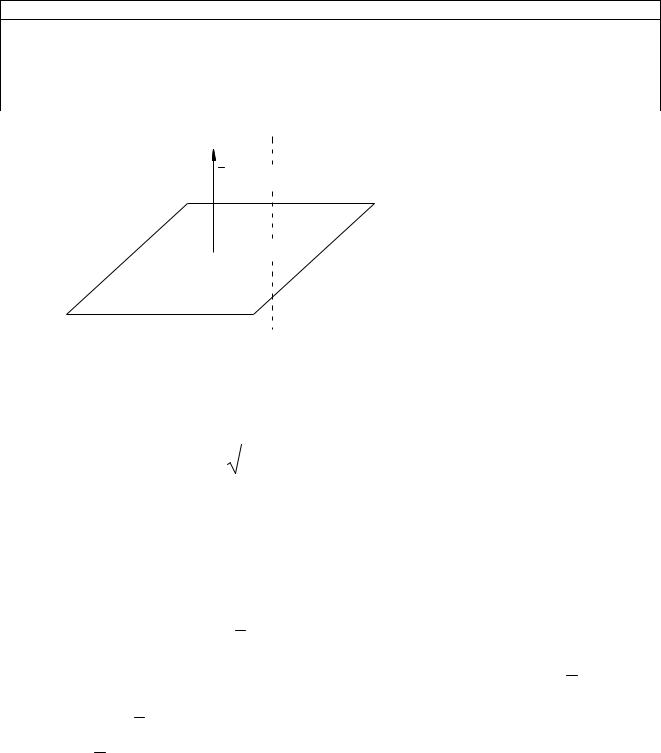
Задача 4. Найти расстояние от точки M0(x0; y0; z0) до плоскости

Ax By Cz D 0(рис 9.8) .

Поскольку расстояние от точки до плоскости есть проекция вектора соединяющего эту точку и любую точку на плоскости на нормальный вектор

плоскости, поэтому d

пр

M0M1

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Разработала:	Идентификационный	Контрольный экземпляр	Лист
	номер:	находится на кафедре	стр. 90 из 172
Дегтярева Н.Е.		Алгебры, геометрии и
		анализа