Конспект лекций по алгебре

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

1 1i i 1 2i j 1 3i k

2 1 j i 2 2 ˆj j 2 3 j k

3 1k i 3 2k j 3 3k k

=(учитывая выше записанные равенства, упрощаем полученное

выражение)

i( 2 3 3 2) j( 3 1 1 3) k( 1 2 2 1)

Вместо i, j, k можно взять любой ортонормированный базис.

Теорема (о коллинеарных векторах). Если два вектора коллинеарны, то их координаты пропорциональны:

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

пропорцию 1 2 3 .

1 2 3

Геометрический смысл векторного произведения

1 4 a b 14 a b 1 18 а b

2 2

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

9 2 5 2 45. 2

Смешанное произведение

Определение. Под смешанным произведением векторов a,b,c

Sосн a b ab sin – площадь основания, H c cos – высота параллелепипеда, - угол между вектором c и вектором a b (рис. 6.2),

тогда V ab sin c cos (a b,c).

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

a b c b a c c a b c b a a c b .

Данное свойство следует из антикоммутативности векторного

произведения.

a b c

1( 2 3 3 2) 2( 3 1 1 3) 3( 1 2 2 1)=

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Определение. Вектор [a,[b,c]] a (b c)– называется двойным

векторным произведением.

Свойства двойного векторного произведения

1) [a,[b,c]] (a,c)b (a,b)c;

3) (a b)2 a2b 2 (a b)2.

Оразмерностях векторных величин

Вприложениях математики рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил, которые имеют определенные размерности. Напомним основные правила действий с размерностями:

1)сумма имеет ту же размерность, что и слагаемые, и складывать можно векторные величины одинаковых размерностей;

2)при умножении вектора на скалярную величину их размерности перемножаются;

3)модуль векторной величины имеет ту же размерность что и вектор;

4)скалярное и векторное произведение имеют размерность равную произведению размерностей сомножителей.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Лекция 7

Аналитическая геометрия на плоскости. Алгебраические линии и плоскости. Уравнения прямой на плоскости.

Цель: Изучить понятия алгебраической линии и алгебраической поверхности, виды уравнений прямой на плоскости и их основные характеристики.

Определение. Уравнение (х, у) 0 называется уравнением линии L

на плоскости (относительно заданной системы координат), если этому уравнению удовлетворяют координаты (x, y) любой точки, лежащей на

i 1

k, l 0,1, 2,.., n - показатели степени все целые неотрицательные числа,

алгебраической линии

Всякая неалгебраическая линия называется трансцендентной.

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

Определение. Линией п-го порядка называется алгебраическая линия,

определяемая в декартовой прямоугольной системе координат алгебраическим уравнением п-ой степени с двумя неизвестными.

Определение: Алгебраической называется множество, которое в какой-

либо декартовой прямоугольной системе координат определяется

алгебраической поверхности.

О пересечении двух линий

Пусть даны две линии L1 и L2, заданные соответствующими

уравнениями: 1(х, у) 0 и 2(х, у) 0. Для нахождения всех точек

1(х, у) 0

пересечения L1 и L2 следует решить систему

2(х, у) 0

Уравнение прямой через заданную точку и вектор нормали

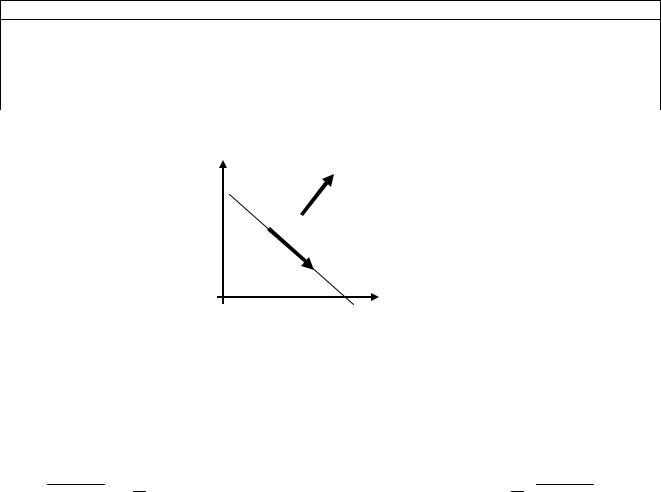
Определение: Всякий ненулевой вектор п L ортогональный прямой,

с координатами (A; B), называется нормалью к прямой (рис. 7.1).

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Учебно-методический комплекс дисциплины Аналитическая геометрия и алгебра

y М0 n

М

x

т.к. M0M n, то их скалярное произведение равно нулю n M0M 0.

Записав его в координатной форме, получим уравнение прямой через точку и вектор нормали

Общее уравнение прямой

Раскрывая в уравнении (7.1) скобки и обозначив Ax0 By0 C

получим общее уравнение прямой:

пропорциональны.