Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Университет им. П.Г. Демидова

Предмет:

Математический анализ

Файл:

Курс лекций по мат. анализу I

.pdf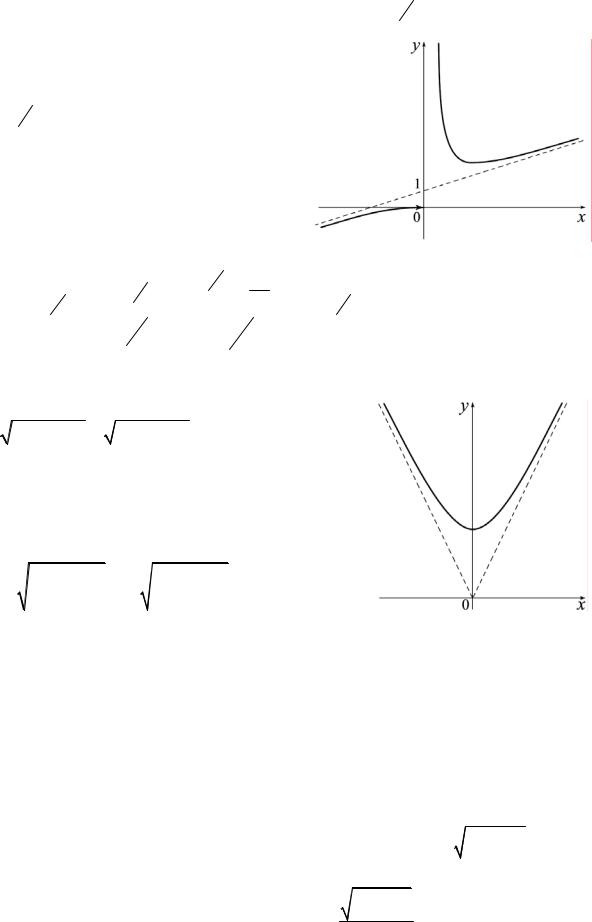

Скачиваний:

Добавлен:

17.03.2015

Размер:

2.49 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 1918 19 > Следующая >>>

Пример 7. Найти асимптоты графика функции f (x)= xe 1x .

☺ Сначала найдем ее наклонные асимптоты. Используя формулу Тейлора, представим функцию в виде

f (x)= xe	1		+	1			1	= x	+1 + o(1).
		x = x 1		x	+ o
						x
Следовательно, прямая							y = x +1		будет на-

клонной асимптотой нашей функции. Вертикальные асимптоты следует ис-

кать там, где функция имеет разрыв, т.е. в

нашем случае в точке x = 0 . С помощью правила Лопиталя найдем предел

−

+∞,

x → 0 + 0,

lim

= lim

= lim e

x =

−

x → 0 −0.

x→0

Следовательно, прямая

x = 0 является

правосторонней

асимптотой графика

нашей функции. ☻

Пример

Найти асимптоты

графика

функции

f (x)= x2 + x + 2 + x2 − x + 2 .

☺ Функция определена на всей вещественной оси и не имеет точек разрыва. Поэтому вертикальных асимптот нет.

Для нахождения наклонных асимптот используем формулу Тейлора:

f (x)=

1 +

1 − 1 +

1 1

1 +

+ o

+ 1

−

+ o

2 x

= 2

+ o(1).

Это

означает, что функция

имеет две

наклонные

асимптоты

y = 2x , если x → +∞ и y = −2x , если x → −∞. ☻

Если угловой коэффициент наклонной асимптоты равен нулю, то получается горизонтальная асимптота, которую мы будем считать частным случа-

ем наклонной. В этой ситуации достаточно сразу искать b = lim f (x), если он

x→∞

конечен.

3	(x −3)2
Например, функция, рассмотренная в примере 1, f (x)=			имеет
	x2
		− 4

3 (x −3)2

горизонтальную асимптоту y = 0 , так как k = lim ( )= 0 и

x→∞ x x2 − 4

170

(x −1)3

3	(x −3)2
b = lim			= 0 .
	x2
x→∞		− 4

Очевидно, что асимптоты графика функции характеризуются следующим свойством: Расстояние от точки M (xM , yM ), лежащей на

графике до асимптоты стремится к нулю при условии, что точка графика уходит в бесконеч-

ность, т.е. xM2 + yM2 → ∞.

7.6.Исследование функции и построение графика

Изучение поведения функции целесообразно проводить по следующему

плану:

1.Найти область определения функции и ее точки разрыва.

2.Отметить такие свойства, как четность, нечетность, периодичность (если они есть).

3.Вычислить первую производную и найти промежутки возрастания и убывания функции, а также ее экстремумы.

4.Найти вторую производную и исследовать функцию на выпуклость. Найти точки перегиба функции.

5.Найти асимптоты графика функции.

6.Если надо, найти дополнительные точки, например, точки пересечения графика с координатными осями.

7.Построить график.

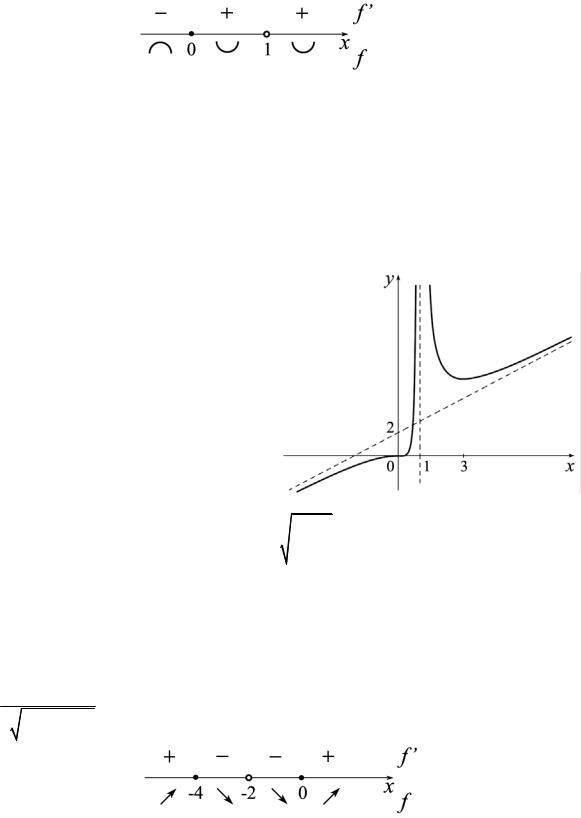
Пример 9. Исследовать функцию f (x)=	x3	.
	(x −1)2

☺1) Область определения этой функции D( f )= (−∞,1) (1, +∞). Точка

x=1 - точка разрыва функции.

2)Функция не является ни четной, ни нечетной.

3)Исследуем функцию на монотонность и экстремумы. Для этого найдем про-

изводную: f ′(x)= x2 (x −3) и исследуем ее знак.

Функция возрастает на промежутке (−∞,1) и на промежутке [3, +∞), и убывает на промежутке (1,3]. В точке x = 3 функция имеет минимум, причем f (3)= 278 .

171

4)		Исследуем		выпуклость этой функции. Найдем ее вторую производную:
	′′		6x
f		(x)= (x −1)4		и исследуем ее знак.

Функция выпукла вверх на промежутке (−∞,0) и выпукла вниз на каждом из промежутков (0,1) и (1, +∞). Точка x = 0 - точка перегиба функции и f (0)= 0 .

5) Найдем асимптоты графика функции. Сначала возьмем точку разрыва функции и найдем предел функции при x , стремящемся к этой точке:

lim

= +∞, следовательно, прямая

x =1 является вертикальной асимпто-

(x −1)2

x→1

той графика. Для нахождения наклонной

асимптоты выделим целую часть из дро-

би

f (x)=

= x + 2 +

3x + 2

. Так

(x −1)2

как

lim

3x + 2

= 0 , то прямая y = x + 2

x→∞

(x −1)2

является наклонной асимптотой.

6) Теперь можно построить график

функции. ☻

Пример 10.

Исследовать функцию f (x)= 3

x + 2

☺ 1)

Область определения этой

функции D( f ) = (−∞, −2) (−2,+∞).

Точка x = −2 является точкой разрыва этой функции.

2)Функция не является ни четной, ни нечетной.

3)Исследуем функцию на монотонность и экстремумы. Найдем производную:

f	′	(x)=	x + 4	и исследуем ее знак.
			33 x(x + 2)4

Функция возрастает на промежутке (−∞, −4] и на промежутке [0, +∞), и убывает на промежутке [−4, −2) и на промежутке (−2,0]. Точка x = −4 - точка

172

максимума, причем				f (−4) = −2 , а точка x = 0 - точка острого минимума.
f	(0) = 0 .
4)	Исследуем функцию на выпуклость. Найдем вторую производную.
f ′′(x)=		−2	(x + 4 − 2 3 )(x + 4 + 2 3 )		и исследуем ее знак
			93 x4	(x + 2)7

Функция выпукла вниз на промежутке (−∞, −4 − 2 3 ) и на промежутке

(−2, −4 + 2

3 ),

выпукла

вверх

на

каждом

из

промежутков

(−4 − 2 3, −2), (−4 + 2

3,0) и

(0, +∞). Точки

x = −4 ± 2

являются точками

перегиба.

(−4 + 2

3 )≈ 0,6 и

f (−4 − 2

3 )≈ −2,1.

5) Прямая

x = −2

является вертикальной

асимптотой

графика,

так

как

lim 3

= ∞. Для удобства построения

x + 2

x→−2

графика, найдем односторонние пределы:

lim

= −∞

lim 3

= +∞ .

x +

x + 2

x→−2−0

x→−2+0

Наклонных

асимптот

нет,

так

как

f (x) 3 x при x → ∞.

6) Построим график (отмечены точки пе-

региба). ☻

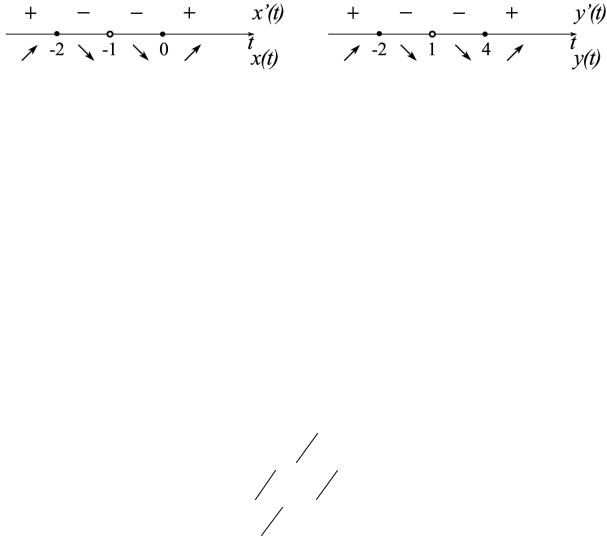
Пример 11. Построить кривую, заданную параметрически:

x(t )

y(t )= t2 −t +9 .

t +1

t −1

☺1)

Кривая

определена

при

t ≠ ±1, т.е. состоит

из

трех

ветвей: для

t (−∞,−1), для t

(−1,1)

и для t (1, +∞).

2) Найдем сначала асимптоты кривой.

x → −∞,

y → −5,5 при t → −1 −0 , и x → +∞,

y → −5,5 при t → −1 + 0 , следова-

тельно, прямая y = −5,5 является горизонтальной асимптотой.

Аналогично,

если

t →1 −0 , то

x →

1 ,

y → −∞, и, если

t →1 + 0 , то x → 1 ,

y → +∞, следовательно, прямая x =

является вертикальной асимптотой.

173

Обе переменные x и y

стремятся к бесконечности только при t → ∞. По-

этому

параметры

наклонной

асимптоты

найдем

при

t →∞:

k = lim

y(t )

= lim

(t2 −t +9)(t +1)

=1 и

(t −1)t2

t→∞ x(t )

t→∞

−t +

8t +9

b = lim

(y(t )− kx(t ))= lim

−

= lim

=1.

Отсюда, пря-

t→∞

t −1

t +1

t→∞

−1

мая y = x +1 - наклонная асимптота кривой.

3) Найдем

производные от функций

x(t ) и

y(t )

по

переменной

t :

x′(t )=

t (t + 2)

y′(t )=

(t − 4)(t + 2)

, и две первые производные от

y по

x :

(t +1)2

(t −1)2

y′x =

(t − 4)(t +1)2

, при t ≠ −2 и y′′xx =

(t +1)3 (16t − 4)

t (t −1)2

t3 (t + 2)(t −1)3

Исследуем функции x(t ) и y(t ) на монотонность.

Так как функции x(t )

y(t )

определяют функцию

y(x)

на тех промежутках

изменения переменной t ,

где x(t ) монотонна, то можно сказать,

что в нашем

случае

мы

имеем

три

функции:

y1 (x)

при

t (−∞, −2],

y2 (x) при

t [−2, −1) (−1,0] и y3 (x) при t [0, +∞).

Найдем

некоторые

точки,

лежащие

на

кривой:

M1 (x(−2)= −4, y(−2)= −5);

M2 (x(0)= 0, y(0)= −9),

M3 x

, y = −

M4 x(4)

, y(4)= 7 .

Теперь составим сводную таблицу изменения параметров искомой кривой

x(t )

y(t )

(−∞, −2)

x(t ) возрастает от −∞ до −4

y(t )

возрастает от −∞ до −5

(−2, −1)

x(t ) убывает от −4 до −∞

y(t )убывает от −5 до −5,5

(−1,0)

x(t ) убывает от +∞ до 0

y(t )

убывает от −5,5 до −9

(0,1)

x(t ) возрастает от 0 до 12

y(t )

убывает от −9 до −∞

(1,4)

x(t ) возрастает от 12 до 16 5

y(t )

убывает от +∞ до 7

(4, +∞)

x(t ) возрастает от 16 5 до +∞

y(t )

возрастает от 7 до +∞

174

t (t −1)2

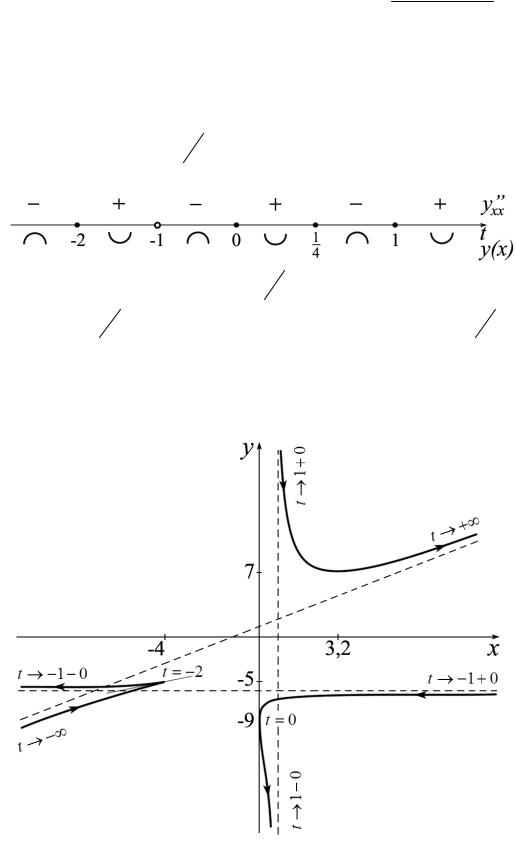
При t = 4 производная y′x = 0 и меняет знак с «-» на «+», поэтому соответствующая точка кривой является точкой минимума.

При t = 0 производная y′x = ∞, поэтому найдем x′y = (t − 4)(t +1)2 , t ≠ −2 . В точке t = 0 эта производная равна нулю и меняет знак с «-» на «+», поэтому эта часть кривой, рассматриваемая как функция x = x(y), имеет минимум в со-

ответствующей точке.

При t = −2 производной y′x не существует, но существуют ее предельные значения справа и слева, равные 13 .

4). Исследуем на знак вторую производную y′xx′ :

На промежутках (−∞, −2), (−1,0) и (14 ,1) кривая выпукла вверх, на про-

межутках (−2, −1), (0, 14) и (1, +∞) кривая выпукла вниз. При t = 14 вторая

производная y′′xx равна нулю и меняет знак, следовательно, в соответствующей точке кривая имеет перегиб. Строим график функции.☻

175

§8 Векторная функция скалярного аргумента

8.1.Определения

Определение 4.8.1. Если каждому значению t G , где G , ставится в соответствие вектор r (t ) трехмерного пространства, то будем говорить, что на

множестве G задана векторная функция r (t ) скалярного аргумента t или вектор-функция r (t ).

Если в пространстве задана прямоугольная система координат, то задание векторной функции r (t ) равносильно заданию трех координатных функций

x(t ), y(t ) и z (t ). Это можно записать в виде r (t ) = (x(t ), y(t ), z (t )) или, используя координатные орты, r (t ) = x(t )i + y(t ) j + z (t )k .

Если z (t ) = 0, t G , то функцию r (t ) называют двумерной.

Будем считать, что начало вектора r (t ) находится в начале координат, т.е. векторы r (t ) являются радиус-векторами. Тогда множество концов этих векторов называют годографом вектор-функции.

Символом r (t ) будем обозначать длину вектора r (t ), т.е. r (t ) = x2 (t )+ y2 (t )+ z2 (t ).

8.2.Предел и непрерывность

Определение 4.8.2. Вектор a

называют пределом вектор-функции r (t ) при

t →t0 , если lim

r (t )− a

= 0 .

t→t0

Записывать этот факт будем следующим образом a = lim r (t ).

Теорема 4.8.1. Вектор a = (a1, a2 , a3 )

t→t0

тогда и только тогда будет пределом

вектор-функции

r (t )

при

t →t0 ,

когда

x(t ) →a , y

(t ) →a

, z (t ) →a .

t→t0

► Пусть

a = lim r (t ),

т.е.

lim

r (t )− a

= 0 .

Тогда

x(t ) →a1 ,

t→t0

y(t ) →a , z (t ) →a

так как

t→t0

x(t )− a1

≤

(x(t )− a1 )2 +(y(t )− a2 )2 + (z (t )− a3 )2 ,

y(t )− a2

≤

(x(t )− a1 )2 +(y(t )− a2 )2 +(z (t )− a3 )2 ,

z (t )− a3

≤

(x(t )− a1 )2 +(y(t )− a2 )2 + (z (t )− a3 )2 .

176

Обратно, если x(t ) →a , y (t ) →a					,	z (t ) →a , то
	t→t0	1	t→t0	2		t→t0	3
r (t )− a	= (x(t )− a1 )2 +(y(t )− a2 )2 +(z (t )− a3 )2 → 0 . ◄
r (t )− a	= (x(t )− a1 )2 +(y(t )− a2 )2 +(z (t )− a3 )2 → 0 . ◄
			t→t
			0

Очевидно, что для векторной функции выполнено утверждение: для того чтобы вектор a был пределом вектор-функции r (t ) при t →t0 необходимо и

достаточно,

чтобы

вектор-функцию

можно

было

представить

виде

r (t )= a +γ (t ), где γ (t ) → 0 .

t→t0

Свойства пределов вектор-функции

Свойство 1. Если lim r (t )= a , то lim

r (t )

t→t0

r (t )

r (t )− a

Доказательство следует из неравенства

−

≤

Свойство 2. Равенство lim r (t )= 0 равносильно равенству lim

r (t )

= 0 .

t→t0

В одну сторону это свойство следует из свойства 1, а в обратную из опре-

деления предела вектор-функции.

Свойство 3. Если r (t )

- векторная функция, а f (t ) - скалярная функция аргу-

мента t G , причем

t→t

(

)

= a

t→t

(

)

t→t

(

)

(

))

= A

a .

lim r

и lim f

A, то lim

f (t ), по-

► По критерию того, что число A является пределом функции

лучим f (t )= A + β (t ), где β (t )→ 0 при

t →t0 .

Аналогично, r (t )= a +γ (t ), где

lim γ (t )= 0 . Тогда

t→t0

f (t ) r (t )= (A + β (t ))(a +γ (t ))= A a +(β (t )a + Aγ (t )+ β (t )γ (t )),

причем

β (t )a + Aγ (t )+ β (t )γ (t )

≤

β (t )

γ (t )

β (t )

γ (t )

так

)

как

каждая

)

компонента

правой

части

стремится

(

к нулю,

то

(

a + Aγ

(

)

+ β

(

)

→ 0 , следовательно,

t→t0 (

(

)

))

. ◄

A a = lim

Свойство 4. Если lim r

(t )= a и

lim r

(t )

= a

, то

t→t

t→t 2

a) lim

(r1 (t )+ r2 (t ))= a1 + a2 ;

t→t

(r1 (t ) r2 (t ))= a1 a2 ;

б) lim

t→t

в) lim (r1 (t )×r2 (t ))= a1 ×a2 .

→t

► Формула a) очевидно следует из того, что по условию можно записать

r1 (t )= a1 +γ

(t ) и r2 (t )

= a2

+γ

(t ), где lim γ

(t )= lim γ

(t )= 0 .

t→t

Для доказательства формулы б) используем эти же представления векторных функций и свойства скалярного произведения:

177

r1 (t ) r2 (t )− a1 a2 = (a1 +γ1 (t ))(a2 +γ2 (t ))− a1 a2 =

= a1 γ2 (t )+ a2 γ1 (t )+γ1 (t ) γ2 (t )

Так как выполнено неравенство (a b ) ≤ a b , то правая часть разности стремится к нулю.

Формула в) доказывается аналогично, так как (a ×b ) ≤ ab . ◄

Определение 4.8.3. Вектор-функцию r (t ) будем называть непрерывной в

точке t = t0 , если lim r (t )= r (t0 ).

t→t0

Пусть дана вектор-функция r (t ), определенная в некоторой окрестности точки t = t0 . Разность ∆r (t0 )= r (t0 + ∆t )− r (t0 ) будем называть приращением вектор-функции r (t ) в точке t = t0 .

Очевидно, что вектор-функция непрерывна в точке t =t0 тогда и только

тогда, когда lim ∆r (t0 )= 0 .

∆t→0

Очевидно также, что непрерывность векторной функции в точке t =t0

равносильна непрерывности в этой точке координатных функций x(t ), y(t ), z (t ).

8.3. Производная и дифференциал

Определение 4.8.4. lim ∆r (t0 ), если он существует, называют производной

∆t→0 ∆t

вектор-функции r (t ) в точке t =t0 и обозначают r′(t0 ), ri (t0 ), или drdt(t0 ).

Таким образом, r′(t0 )= lim r (t0 + ∆∆tt)− r (t0 ).

∆t→0

Из свойств пределов следует, что r′(t0 )= (x′(t0 ), y′(t0 ), z′(t0 )).

Из определения производной получим ∆r (t0 )= r′(t0 )∆t +γ (∆t )∆t , где

lim γ (∆t )= 0 . Отсюда следует непрерывность векторной функции в каждой

∆t→0

точке, где эта функция имеет производную.

Произведение r′(t0 )∆t будем называть дифференциалом векторной

функции, а функцию, имеющую дифференциал, - дифференцируемой. Выясним геометрический смысл производной векторной функции. Пусть r (t ) векторная функция, дифференцируемая в точке t = t0 , причем

r′(t	0	)≠ 0 . На	годографе функции r (t )	построим	точки M	0	(x , y , z			0	) и
	0					0		0	0	0
M1 (x1, y1, z1 ), где x0 = x(t0 ), y0 = y(t0 ), z0 = z (t0 ) и x1 = x(t0 + ∆t ),						y1 = y(t0 + ∆t ),
z1 = z (t0 + ∆t ).			Тогда прямая M0M1	называется	секущей,			а	вектор
			178

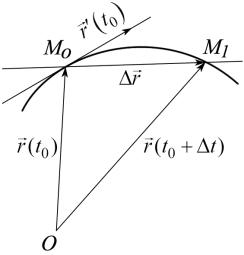
∆r (t0 )= r (t0 + ∆t )− r (t0 )= M0M1 - вектором секущей. Если r′(t0 ) ≠ 0 , то в некоторой окре-

стности точки			t =t0	вектор	∆r (t0 )≠ 0	и отно-
шение	∆r (t0 )		≠ 0 .	Тогда	параметрическое
	∆t

уравнение секущей				можно	записать	в виде
r (λ)= r (t0 )+		∆r (t0 )		λ, λ .

			∆t
При ∆t → 0 точка M1					будет перемещать-

ся по кривой и стремиться к точке M0 . При

этом секущая будет поворачиваться и стремится занять предельное положение, которое мы будем называть касательным. Таким образом, если существует

r′(t0 )≠ 0 , то, переходя к пределу в уравнении секущей, получим уравнение ка-
сательной r (λ)= r (t0 )+ r′(t0 )λ, λ			или в канонической форме
	x − x0	=	y − y0	=	z − z0	.
	x′(t0 )		y′(t0 )
					z′(t0 )
Таким образом, мы доказали, что r′(t0 )				- вектор касательной к годогра-

фу функции r (t ) в точке M0 (x0 , y0 , z0 ) и, что этот вектор существует, если

r′(t0 )≠ 0 .

Замечание. Иногда под понятием «касательная» понимается касательный вектор. Так как график обычной функции можно понимать, как кривую, заданную параметрически (где в качесве параметра берется x ), то при таком подходе, то при таком подходе функция не будет иметь касательную в точках, где ее производная бесконечна, но знак этой бесконечности не определен.

Теорема 4.8.2. Если функции r1 (t ), r2 (t )						и	f	(t )	имеют производные в точке t ,
то в этой точке справедливы формулы
a) (r	+ r		)′ = r′ + r ′;
1	2		1		2
б) ( f r )′ = f ′ r + f r′;
в) (r	r )′ = r′ r + r						r ′;
1	2		1	2		1		2
г) (r	×r	)′ = r′		×r		+ r		×r	′.
1	2		1	2			1	2

Доказательство теоремы легко следует из определения производной и свойств скалярного и векторного произведений, и предоставляются читателю.

179

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 1918 19 > Следующая >>>

Соседние файлы в предмете Математический анализ

#
17.03.20151.06 Mб651 - 20.doc
#
17.03.201528.67 Кб18matan2-12.doc
#
17.03.201514.02 Кб24Voprosy_po_matanu_2_semestr.docx
#
06.03.20163.65 Mб549Бондаренко В.А., Шабаршина Г.В. - Математический анализ. Предел и непрерывность.doc
#
17.03.201526.62 Кб12Вопросы Матан.doc
#
17.03.20152.49 Mб84Курс лекций по мат. анализу I.pdf