
Курс лекций по мат. анализу I
.pdf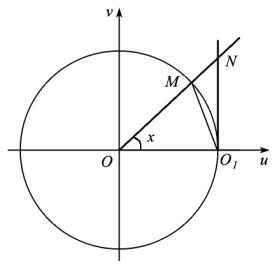
arth x = |
1 ln |
1 + x , |
|
x |
|
<1 и |
|||
|
|
||||||||
|
2 |
1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
arcth x = 1 ln 1 + x |
, |
|
x |
|
>1. |
||||
|
|
||||||||
|
2 |
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8) Тригонометрические функции были достаточно хорошо определены в школе, и мы будем считать, что эти определения хорошо известны. Выведем несколько полезных свойств тригонометрических функций.
Свойство 1. sin x < x < tg x при 0 < x < |
π |
, |
|
sin x |
|
≤ |
|
x |
|
≤ |
|
tg x |
|
|
− |
π |
, |
π |
и |
|||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
при x |
|
|
|||||||||||||||||
|
sin x |
|
≤ |
|
x |
|
при любом x. |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
►Рассмотрим на тригонометрической окружности угол x , лежащий в первой четверти (изображено на рисунке). Пусть дуга O1M равна x . Построим
линию тангенсов и отложим на ней точку N такую, что O1N = tg x . Рассмотрим треугольники OMO1 , ONO1 и сектор OMO1 . Очевидно, что площади этих фигур
связаны |
|
|
|
|
|
|
неравенством: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
S OMO |
< ScekmOMO < S ONO . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как эти площади равны, соответственно: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
S OMO = |
1 R2 sin x = 1 sin x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ScekmOMO |
= |
1 R2 x = |
1 x |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
ONO |
= |
|
1 OO O N = 1 tg x , то из неравенст- |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
1 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ва между площадями получим неравенство |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
sin x < x < tg x, |
0 < x < π . |
(*) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Используя нечетность функций sin x и |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
tg x , |
получим, |
что |
если |
−π < x < 0 , |
|
то |
выполнено |
неравенство |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
−sin x < −x < −tg x |
или |
|
sin x |
|
< |
|
|
|
|
|
x |
|
< |
|
tg x |
|
. |
|
|
|
Тогда, |
очевидно, |
что, если |
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x |
|
π |
, |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
, то справедливо неравенство |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
≤ |
|
|
x |
|
|
≤ |
|
tg x |
|
|
|
(**) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
и x |
|
имеет место неравенство |
|
sin x |
|
≤ |
|
x |
|
. ◄ |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Свойство 2. Тригонометрические функции непрерывны на своих областях определения.
►Рассмотрим приращение функции sin x :
∆f (x)= sin (x + ∆x)−sin x = 2sin ∆2x cos x + ∆2x .
120

Используя |
|
|
|
|
неравенство |
(**) |
и |
|
|
то, |
что |
|
cos |
|
|
|
|
∆x |
|
|
≤1, получим |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x + |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∆f (x) |
|
≤ 2 |
|
∆x |
|
= |
|
∆x |
|
|
. Отсюда следует, что, если ∆x → 0 , то ∆f (x)→ 0 . |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Аналогично получается неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(x + ∆x)−cos x |
|
= |
|
2sin |
∆x |
sin |
|
∆x |
|
≤ |
|
∆x |
|
, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x + |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
из которого следует непрерывность функции cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Функции tg x |
|
|
и ctg x непрерывны в точках, где они существуют, как ча- |
|||||||||||||||||||||||||||||||||||||||||||
стные непрерывных функций.◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Свойство 3 (Первый замечательный предел) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim sin x =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
►Считая, что |
|
|
|
x ≠ 0 , разделим каждый член неравенства (**) на |
|
sin x |
|
и |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
получим 1 |
< |
|
|
|
|
x |
|
< |
1 |
|
или 1 |
> sin x > cos x , x (−π |
2 |
,π |
2 |
), x ≠ 0 . Так как |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
sin x |
|
|
|
cos x |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
все функции в последнем неравенстве положительны, то модуль можно убрать и получить 1 > sinx x > cos x . Если устремить x к нулю, то cos x будет стремить-
ся к 1 (по непрерывности функции cos x ). Следовательно, по теореме о сжатой
переменной будет иметь место равенство lim sin x =1, которое обычно называ-
x→0 x
ют первым замечательным пределом. ◄
9) Обратные тригонометрические функции
Рассмотрим функцию f (x)= sin x , x −π 2 ,π 2 . Известно, что такая функ-
ция строго возрастает и непрерывна, следовательно, она имеет обратную, которая также будет возрастать и будет непрерыв-
ной |
и |
[ |
которая |
обозначается |
|
arcsin x, x |
−1,1 . |
|
|||
|
|
|
] |
|
|
|
[ |
Аналогично, функцией arccos x , |
|||
x |
] |
|
|
|
|
|
−1,1 будем называть функцию, обрат- |
||||
ную к функции cos x, x [0,π]. Эта функ-
ция будет непрерывной и строго убывающей.
121
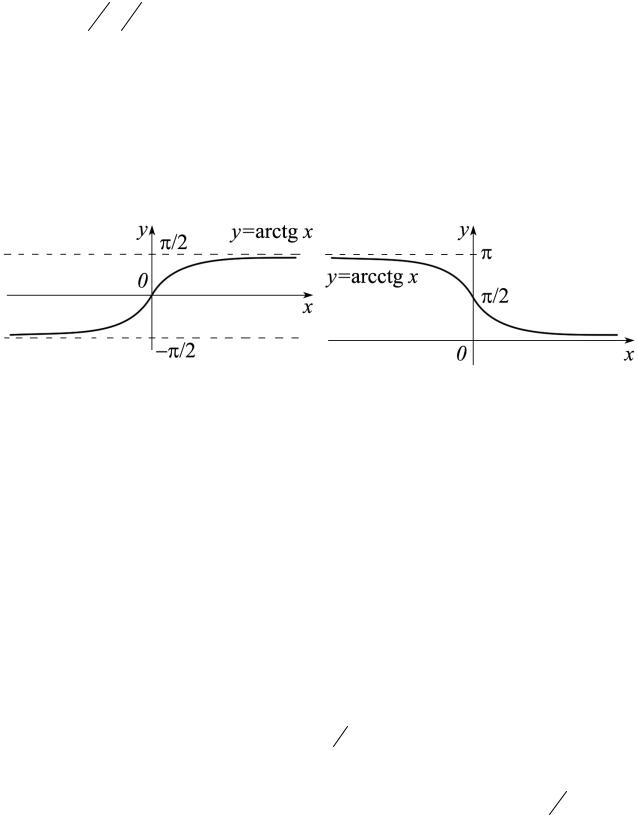
Функцией arctg x, x будем называть функцию, обратную к функции tg x, x (−π 2 ,π 2), а функцией arcctg x, x - функцию, обратную к функции
ctg x, x (0,π ). Эти функции непрерывны и монотонны.
В заключении отметим два полезных равенства с обратными тригонометрическими функциями.
1.arcsin x + arccos x = π2
2.arctg x + arcctg x = π2 .
►Докажем первое равенство. Докажем, |
что |
π |
−arccos x = arcsin x . Оче- |
|||||||||
|
π |
|
|
|
|
π |
2 |
π |
|
π |
|
|
видно, |
= cos(arccos x)= x |
и |
− |
≤ |
−arccos x ≤ |
. Отсюда |
||||||
sin |
−arccos x |
2 |
2 |
2 |
||||||||
|
2 |
|
|
|
|
|
|
|
||||
π2 −arccos x = arcsin x .
Второе равенство доказывается аналогично. ◄
5.3. Некоторые важные пределы
Выше мы доказали, что lim sin x =1. Рассмотрим еще несколько важных
x→0 x
пределов.
1). Второй замечательный предел
lim (1 + x)1x = e .
x→0
► В теореме 2.4.1. было доказано, что для любой бесконечно малой чи-
словой последовательности {xn} |
будет верно равенство lim (1 + xn ) |
1x |
n |
= e . То- |
|||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
гда требуемое утверждение следует из определения предела по Гейне. ◄ |
|||||||
2). |
lim |
ln (1 + x) |
=1. |
|
|
|
|
|
|
|
|
||||
|
x→0 |
x |
|
|
|
|
|
|
122 |
|
|
|
|
|
|

|
► Функция |
|
ln (1 + x) |
|
не определена в точке x = 0 , но мы можем исполь- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t ) непрерывна: |
||||||||
зовать |
свойство |
сложной |
|
|
функции |
|
при |
|
|
условии, что |
|
||||||||||||||||||||||||||||||||||||||||||
lim f |
(g (x)) |
= f |
lim g (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x→x0 |
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Используя |
|
|
непрерывность |
|
логарифмической |
|
|
|
функции, |
получим |
||||||||||||||||||||||||||||||||||||||||||
|
ln (1 + x) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim |
|
|
|
|
|
= lim ln (1 + x) |
|
|
x |
= ln |
lim (1+ x) |
|
|
x = ln e |
=1. ◄ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x→0 |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следствие. lim |
loga (1 + x) |
= |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
► lim |
loga (1 + x) |
= lim |
ln (1 + x) |
= |
|
1 |
|
lim |
ln (1 + x) |
|
= |
|
1 |
|
. ◄ |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ln a |
|
|
|
ln a |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
x→0 |
|
|
|
x |
|
|
|
|
x→0 |
|
xln a |
|
|
|
|
|
|
x→0 |
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
ex −1 |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
► Пусть ex −1 = y . Тогда x = ln (1 + y). Заметим также, что утверждение |
||||||||||||||||||||||||||||||||||||||||||||||||||||
x → 0 |
равносильно утверждению |
y → 0 . Поэтому |
|
lim |
ex −1 |
= lim |
|
y |
=1. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
y→0 ln (1 + y) |
|
|||||||
◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следствие. lim |
|
ax −1 |
= ln a, |
|
|
a > 0, a ≠1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
► lim |
ax − |
1 |
= lim |
ex ln a −1 |
|
|
|
= ln a lim |
ey −1 |
= ln a . |
Здесь |
положено |
||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
xln a |
|
|
|
ln a |
|
|
y |
||||||||||||||||||||||||||||||||||||||
|
|
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y = xln a → 0 . ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
(1 + x)s −1 |
= s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
s |
|
|
|
|
|
|
|
|
|
|
s ln(1+x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s ln(1+x) |
|
|
|
|
|
|
|
|
|
||||||||||
lim (1 + x) |
|
|
|
|
|
|
|
|
|
e |
−1 |
|
s ln (1 + x) |
|
|
|
|
|
|
|
e |
−1 |
|
|
ln (1 + x) |
|
|
||||||||||||||||||||||||||
|
−1 = lim |
|
|
|
|
|
|
|
|
|
= s lim |
|
|
|
|
lim |
= s . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x→0 |
|
x |
|
|
|
|
|
|
x→0 |
|
s ln |
(1 + x) |
|
|
|
|
x |
|
|
|
|
|
|
x→0 s ln (1 |
+ x) x→0 |
x |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
◄
123

§6 Сравнение функций. Символы Ландау
6.1.Сравнение функций
Определение 3.6.1. Пусть функции f (x) и g (x) определены в некоторой про-
колотой окрестности |
o |
) точки |
x . Будем говорить, что функция |
U (x |
|||
|
0 |
|
0 |
f (x) = O(g (x)) (читается: функция f |
(x) есть О большое от функции g (x)) |
||
при x , стремящемся к x0 , если существует функция h(x), определенная в той
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
||
же окрестности точки x0 |
такая, что x U (x0 ) |
|
выполняется равенство |
||||||||||||||||
f (x) = h(x) g (x) и |
|
h(x) |
|
≤ C . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 1. |
x + 2x = |
|
O( |
|
|
x ) |
при x → 0 . |
|
|
|
|
|
|
|
|
||||
☺ |
x + 2x = |
|
x (1 + 2 |
x ) и в окрестности нуля функция h(x) =1 + 2 x |
|||||||||||||||
ограничена. ☻ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2. |
x + 2x = O(x) |
при x → ∞. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
. При x → ∞ сумма |
|
|
1 |
|
|
|
|
||||
☺ x + 2x = x |
2 + |
|
|
|
|
|
|
2 + |
|
|
|
|
будет ограниченной.☻ |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|||||
Пример 3. |
xsin 1 = O(x) |
|
|
при x → 0 . |
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
☺ h(x)= sin 1 |
|
ограничена. ☻ |
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
|
|
f (x)= O(1) при x → x0 |
|
|
|
|
|
|
f (x) |
|||||||
Замечание. Равенство |
означает, что функция |
||||||||||||||||||
ограничена в некоторой проколотой окрестности точки x0 . |
|
|
|||||||||||||||||
Если |
f (x)= O(g (x)) |
и g (x)= O(f (x)) |
при |
|
|
x → x0 , то говорят, что |
|||||||||||||
функции f (x) и g (x) одного порядка. |
|
|
|
|
|
|
f (x) |
|
|||||||||||
Теорема 3.6.1. Если существует конечный, не равный нулю предел lim |
, |
||||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
g (x) |
||
то функции f (x) и g (x) одного порядка при x → x0 .
► Обозначим h(x)= gf ((xx)). Так как существует конечный предел
lim f ((x)), то в некоторой проколотой окрестности точки x0 функция h(x) ог-
x→x0 g x
раничена. ◄
Определение 3.6.2. Пусть функции f (x) и g (x) определены в некоторой про-
o
колотой окрестности U (x0 ) точки x0 . Будем говорить, что функция f (x)
124
есть бесконечно малая по сравнению с функцией g (x) при x → x0 , если суще-
ствует функция h(x), определенная в той же окрестности точки x0 такая,
o |
|
|
|
|
|
f (x)= h(x) g (x) и lim h(x) = 0 . |
что x U (x0 ) |
выполняется равенство |
|||||
|
|
|
|
|
|
x→x |
Если данное определение выполнено, то пишут: f (x) = o0(g (x)), x → x0 |
||||||
(читается: |
f (x) |
есть о малое от g (x) при x , стремящемся к x0 ). |
||||
Если g (x) |
бесконечно малая, то f (x) тоже бесконечно малая и говорят, |
|||||
что f (x) бесконечно малая более высокого порядка, чем g (x). |
||||||
Пример 4. |
x2 + 2x = o(x3 ), x →∞. |
|
||||
Пример 5. |
x2 = o(x), |
x → 0 . |
|
|
||
Пример 6. |
sin |
2 x sin 1 |
= o(x), |
x → 0 . |
|
|
|
|
|
x |
|
|
|
Замечание. Символы O(g (x)) |
и o(g (x)) |
при x → x0 означают не конкретную |
||||
функцию, а класс функций и равенство |
f (x)= o(g (x)) означает только, что |
|||||
функция f (x) |
принадлежит этому классу. Например, запись x2 = o(x) озна- |
|||||
чает, что x2 |
при x → 0 является бесконечно малой функцией более высокого |
|||||
порядка, по сравнению с функцией x . |
|
|||||
Поэтому равенство f (x)= o(g (x)) |
нельзя понимать как обычное равен- |
|||||
ство, в частности нельзя читать это равенство справа налево.
Пример 7. Утверждение o(f (x))= O(f (x)) - верно, а O(f (x))= o(f (x)) - не-
верно.
Символы O и o были введены академиком Ландау и их называют симво-
лами Ландау.
Отметим несколько важных для нас свойств символа o (будем считать, что x → x0 ).
1. o(Cf )= o( f ) |
6. o(f k ) o(f m )= o(f k+m ), k , m |
|||
2. C o( f )= o( f ) |
7. f k o( f )= o(f k+1 ), |
k |
||
3. o( f )+ o( f )= o( f ) |
8. (o( f ))k = o(f k ), |
k |
||
4. o(o( f ))= o( f ) |
9. |
o(f k ) |
= o(f k−1 ), |
k |
f |
||||
5. o(f + o( f ))= o( f )
►Докажем, например, четвертое из этих свойств.
125
Возьмем какую-нибудь функцию g (x)= o(o( f )) и какую-нибудь функ-
цию g1 (x)= o( f ). Это означает, что в некоторой проколотой окрестности точ- |
|||||||||||||||||||||||||||||
ки x0 |
|
выполнены соотношения g (x)=α (x) g1 (x) |
и |
|
g1 (x) = β (x) f (x), |
где |
|||||||||||||||||||||||
lim α |
( |
x |
) |
= lim β |
( |
x |
) |
= 0 . |
Тогда |
g |
( |
x |
) |
= |
( |
α |
( |
x |
) |
β |
( |
x |
)) |
f |
( |
x |
) |
, |
где |
x→x |
|
x→x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(x) =α (x) β (x)→ 0 , что означает, что g (x) = o( f ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Остальные свойства доказываются аналогично. ◄
6.2.Эквивалентность функций
Определение 3.6.3. Пусть функции f (x) и g (x) определены в некоторой про-
o
колотой окрестности U (x0 ) точки x0 . Будем говорить, что функция f (x) эквивалентна функции g (x) при x → x0 , если существует функция h(x), оп-
o
ределенная в той же окрестности точки x0 такая, что x U (x0 ) выполня-
ется равенство f (x) = h(x) g (x) и lim h(x) =1.
x→x0
Эквивалентные функции обозначают символом f g при x → x0 .
Замечания
1.Эквивалентные функции являются функциями одного порядка.
2.Отношение эквивалентности обладает свойствами
a)f f (рефлексивность);
б) |
f |
g g f (симметричность); |
в) |
f |
g, g h f h (транзитивность). |
Используя пределы, найденные в §5, запишем таблицу некоторых эквивалентных функций, которая нам понадобится для вычисления различных преде-
лов. При t → 0 выполнены соотношения |
et −1 t |
|
|
|
sin t t |
|
|
|
|
arcsin t t |
at −1 t ln a |
|
|
|
tg t t |
ln (1 +t ) t |
|
|
|
arctg t t |
loga (1 +t ) |
|
t |
|
|
ln a |
|||
|
|
|
||
1 −cost t2 |
(1 +t )s −1 st |
|||
2 |
|
|
|
|
Доказательства этих соотношений предоставляем читателю. |
||||
Теорема 3.6.2. Если при x → x0 выполнено f f1 и g g1 , то |
||||
1) если существует lim ( f1 g1 ), то lim ( f g )= |
lim ( f1 g1 ) и |
|||
x→x0 |
x→x0 |
x→x0 |
||
126 |
|
|
|
|

|
|
|
|
|
|
2) если существует lim |
|
|
f1 |
|
|
, то lim |
f |
|
|
|
= lim |
|
|
f1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 g |
|
|
|
|
|
|
x→x0 |
|
|
x→x0 |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
►По условию теоремы в некоторой окрестности точки x0 будет выпол- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нено |
|
f (x)= f (x)h |
(x) и g |
(x)= g (x)h (x), где |
|
lim h |
(x)= lim h |
(x)=1. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x→x |
|
|
1 |
|
x→x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
lim ( |
|
|
|
( f1 h1 g1 h2 )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ( f1 g1 ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
f g )= |
lim |
|
lim ( f1 g1 ) lim (h1 h2 )= |
|
|
|
|
|
и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x→x0 |
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
|
f |
|
= |
lim |
|
f1 h1 |
= lim |
f1 |
lim |
|
|
h1 |
|
= lim |
|
|
f1 |
|
|
. ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
g |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x→x0 |
|
g |
x→x0 |
g h |
|
|
x→x0 |
|
x→x0 |
|
|
|
x→x0 |
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 3.6.3 (Критерий эквивалентности функций) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Две функции |
|
f |
(x) |
и g (x) |
|
|
эквивалентны при x → x0 тогда и только то- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
гда, когда при x → x0 |
|
справедливо равенство f (x)= g (x)+ o(g (x)). |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
► Пусть |
|
f g при |
|
x → x0 . |
|
Тогда в некоторой окрестности точки |
x0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
справедливо равенство |
|
f (x)= g (x) h(x), |
|
где |
|
lim h(x)=1. |
|
Отсюда получим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( |
|
) |
|
|
|
( |
|
) |
|
|
( |
|
|
)( |
|
|
|
( |
|
)) |
|
|
|
|
|
|
|
|
|
x→x ( |
|
|
|
|
( |
x→x0 |
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
||||||||||||||
f |
x |
− g |
x |
= g |
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
− h |
x |
)) |
|
= 0 , то |
f − g = o |
g |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 − h |
|
|
|
. Так как |
lim |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратно, пусть |
|
f (x)= g (x)+ o(g (x)) |
|
|
при x → x0 . Тогда в некоторой ок- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рестности точки |
|
|
x0 |
будет |
|
f (x)− g (x)= g (x)α (x), |
|
где |
lim α (x)= 0 . Отсюда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( |
|
) |
|
|
|
( |
|
)( |
|
|
|
( |
|
)) |
|
|
|
|
|
( |
|
|
) |
|
|
|
|
( |
|
) |
|
( |
|
) |
|
|
|
|
|
|
( |
|
|
) |
x→x0 |
|
) |
|
|
x→x |
|
( |
|
) |
|
|||||||||||
f |
x |
= g |
x |
|
|
|
x |
или |
|
f |
x |
= g |
x |
h |
x |
, где h |
x |
=1 +α |
( |
x |
и |
|
|
x |
=1. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 +α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim h |
|
|
|||||||||||||||||||||||||||||||||||||||
Это означает, что |
|
|
f |
g . ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Используя последнюю теорему, перепишем таблицу эквивалентов следующим образом:
sin t = t + o(t ) arcsin t = t + o(t ) tg t = t + o(t )
arctg t = t + o(t )
cost =1 − t2 + o(t2 ) 2
et −1 = t + o(t )
at −1 = t ln a + o(t )
ln (1 +t )= t + o(t )
loga (1 +t )= lnta + o(t ) (1 +t )s −1 = st + o(t )
Покажем, как можно применять эти соотношения на практике для вычисления пределов.
127

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 cos x −sin 2x ln 1 − |
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пример 8. Вычислить lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ex2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
☺ Используя таблицу эквивалентов и свойства o(xk ), запишем |
|||||||||||||||||||||||||||||||||||||||||
3 cos 6x = |
3 1 − 36x |
2 |
|
(x2 )=1 |
− |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
36x |
2 |
|
|
= |
||||||||||||||||||
+ o |
36x |
|
+ o(x2 ) |
+ o |
|
+ o(x2 ) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
=1 −6x2 + o(x2 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
+ o(x2 ), ex |
2 |
−1 = x2 + o(x2 ). |
|||||||||||||||
sin 2xln 1 |
− |
|
|
= (2x + o(x)) |
− |
|
|
|
+ o(x) |
= −x2 |
|
|
|||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда, используя то, что lim |
o(x2 ) |
= 0 , получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 cos x −sin 2x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
6x2 + x2 + o(x2 )−1 |
|
|||||||||||||||||||||
|
ln 1 |
− |
|
|
|
|
−1 |
|
|
|
1 − |
|
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||
|
|
|
|
|
e |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ o |
(x |
2 |
) |
|
|
||||||||||
x→0 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o(x2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
−5x2 + o(x2 ) |
|
|
|
−5 + |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= lim |
= lim |
|
|
|
|
|
|
|
= −5 . ☻ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
o(x2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x→0 x2 + o(x2 ) |
|
x→0 |
1 + |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
128
ГЛАВА IV. ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ И ЕЕ ПРИЛОЖЕНИЯ
§1 Производная и дифференцируемость функции
1.1.Определение производной
Определение 4.1.1. Пусть функция y = f (x) определена в некоторой окрестности точки x0 . Допустим, что существует предел отношения приращения
функции в этой точке к вызвавшему его приращению аргумента, когда послед- |
||||||||||||||||||||||||||||
нее стремится к нулю: |
|
lim |
|
|
f (x0 + ∆x)− f (x0 ) |
. Тогда этот предел называется |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
||
производной функции в точке x0 . |
|
|
|
|
|
|
|
|
|
f ′(x ) |
|
(x ), |
||||||||||||||||
|
Производная функции |
|
|
y = f (x) в точке x обозначается |
, f ′ |
|||||||||||||||||||||||
|
df (x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
x |
|
0 |
||
|
, y′(x |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dx |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0 + ∆x)− f (x0 ) |
|
∆f (x0 ) |
|
|
|
|
|||||||||
|
Таким образом, f ′(x0 ) |
= lim |
= lim |
. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
∆x |
|
|
|
∆x→0 |
∆x |
|
|
|
|||
|
Операция вычисления производной называется дифференцированием |
|||||||||||||||||||||||||||
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 1. Вычислить производную функции f (x) |
= ax2 a) в точке x |
=1; |
|
б) в |
||||||||||||||||||||||||
произвольной точке x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax2 |
|
|
|
|
|
|
||||||||
|
☺ |
a) |
Составим |
приращение функции |
|
в |
точке |
x |
|
=1: |
||||||||||||||||||
∆f (1)= a(1 + ∆x)2 − a 12 = a( |
2∆x +(∆x)2 ). Тогда |
|
|
|
|
|
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
lim |
∆f (1) |
|
= lim |
a |
(2∆x +(∆x)2 ) |
= |
lim a(2 + ∆x)= 2a . |
|
|
|
|
|
|
||||||||||||||
|
∆x |
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
||||||||||||||
|
∆x→0 |
∆x→0 |
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
|
|
||||||||
б) Составим приращение функции в произвольной точке x : |
|
|
|
|
|
|
||||||||||||||||||||||
|
∆f (x)= a(x + ∆x)2 − ax2 = a |
( |
2x∆x +(∆x)2 ). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Тогда |
lim |
∆f (x) |
|
= |
lim |
|
|
a(2x∆x +( |
∆x)2 ) |
|
= lim |
a(2x + ∆x)= 2ax .☻ |
|
|
||||||||||||||
∆x |
|
|
|
∆x |
|
|
|
|
||||||||||||||||||||
|
|
|
∆x→0 |
|
∆x→0 |
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
|||||||||
Замечание. Производная, вычисленная в произвольной точке, является функцией. Если сначала найти эту функцию, а затем вычислить значение производной функции при заданном значении аргумента, то получим производную в конкретной точке. В рассмотренном примере, производная в произвольной точке равна 2ax . Следовательно, в точке x =1 производная будет равна 2ax |x=1= 2a .
Пример 2. Вычислить производную функции f (t )= 3sin (2t +1) в произвольной точке t .
129
