
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
- •§ 1. Понятие неопределённого интеграла
- •§ 2. Основные свойства неопределённого интеграла
- •§ 3. Таблица основных интегралов
- •2. МЕТОДЫ ИНТЕГРИРОВАНИЯ
- •§ 3. Интегрирование по частям
- •Практическое занятие 1.
- •§ 1. Некоторые сведения о многочленах
- •§ 2. Рациональные дроби
- •§ 3. Интегрирование простейших рациональных дробей
- •§ 4. Метод неопределённых коэффициентов
- •§ 5. Интегрирование рациональных дробей
- •Практическое занятие 2.
- •Практическое занятие 3.
- •Практическое занятие 4.
- •Практическое занятие 5.
- •Практическое занятие 6.
- •ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ЛИТЕРАТУРЫ
- •ОТВЕТЫ

Так, например, большое значение в различных приложениях играет
первообразная Ф x от функции |
1 |
x2 / 2 , удовлетворяющая дополни- |
2 |
||
тельному условию Ф o 0 . |
|
|
Эта функция, в частности, встречается в теории вероятностей и называется интегралом вероятностей. Для неё составлены таблицы значений для различных значений аргумента х.
Если первообразная для некоторой функции не является элементарной функцией, то говорят, что интеграл «не берётся» в элементарных функциях.
Практическое занятие 5.
Интегрирование некоторых классов тригонометрических функций. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
Пример 1. Найти интеграл I1 = sin4 xdx
Решение. Для нахождения интеграла применим формулы понижения степени
sin 2 |
1 |
(1 cos 2 ), |
cos2 |
1 |
(1 cos 2 ) |
|
2 |
|
|
2 |
|
к подынтегральной функции; проведем тождественные преобразования под знаком интеграла; применим свойства линейности, инвариантности, метод введения под знак дифференциала и табличные интегралы
dx x c , cos xdx sin x c.
39

I1= sin 4 xdx = (sin 2 x)2 dx
(12 (1 cos2x)2 dx 14 (1 2cos2x cos2 2x)dx 14 ( dx 2 cos2xdx cos2 2xdx)
=14 (x 2 cos 2xdx 1 cos2 4xdx) 14 (x sin 2x 12 ( dx cos 4xdx))
=14 (x sin 2x 12 x 81 sin 4x) c = 14 (32 x sin 2x 18 sin 4x) c
Пример 2. Найти интеграл I2 = cos3 xdx
Решение. Преобразуем подынтегральную функцию:
I2= cos3 xdx = cos 2 x cos xdx (1 sin 2 x) cos xdx
Теперь применим метод введения под знак дифференциала, свойства линейности и инвариантности и табличные интегралы dx x c ,
x dx |
x 1 |
|
c |
|
1 |
|
|||
|
|
|
||
I2= (1 sin 2 x)d(sin x) d(sin x) sin 2 xd(sin x) sin x sin3 x |
c |
|||
|
|
|
3 |
|
Пример 3. Найти интеграл I3= cos 2x cos 3xdx
Решение. Преобразуем подынтегральную функцию по формуле cos cos 12 (cos( ) cos( )),
а затем применим свойство линейности, метод введения под знак дифференциала и табличный интеграл cos xdx sin x c
I3= cos 2x cos 3xdx =
12 (cos x cos 5x)dx 12 ( cos x 15 cos 5xd (5x)) 12 sin x 101 sin 5x c
40

Пример 4. Найти интеграл |
I4 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3cos x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||
Решение. Применим универсальную тригонометрическую подстановку |
|
|
|||||||||||||||||
|
x |
|
|
x |
|
|
|
|
|
2dt |
1 tg |
2 |
x |
|
|
1 |
t 2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
t tg |
|
; |
тогда |
|
arctg t, x 2arctg t, dx |
|
, cos x |
|
|
|
|
|
|
|
. |
||||
2 |
2 |
1 t 2 |
|
|
x |
|
1 |
t 2 |
|||||||||||
|
|
|
|
|
|
|
|
1 tg |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем подынтегральное выражение к новой переменной t и найдем интеграл по новой переменной, применив метод введения под знак диффе-
ренциала и табличный интеграл |
|
dx |
|
|
|
|
|
|
|
1 arctg |
x |
|
c |
|
|
|
|
|
||||||||||||||||||||
a |
2 |
|
|
2 |
|
|
a |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|||||
I4 |
|
|
dx |
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
2dt |
|
|
dt |
|
|
dt |
|
|
||||||||||||
5 |
3cos x |
|
2 |
|
|
3 1 t |
2 |
|
|
2 8t |
2 |
1 4t |
2 |
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
1 t |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2t |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
d (2t) |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
arctg2t c |
|
|
arctg |
2tg |
|
|
|
|
|
c. |
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
1 |
|
|
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 5. Найти интеграл |
|
I5 |
|
|
4 x2 dx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Решение. Для интегрирования применим подстановку x=2sint, откуда
dx=2cos t dt,  4 x2
4 x2 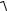 4 4sin2 t 2cost
4 4sin2 t 2cost
Преобразуем данный интеграл к новой переменной t:
I5  4 x2 dx 2cost 2costdt 4 cos2tdt.
4 x2 dx 2cost 2costdt 4 cos2tdt.
Для нахождения полученного интеграла применим формулу понижения степени:
cos2 12 1 cos2 .
I5 4 cos2t dt 4 12 1 cos2t dt 2 1 cos2t dt 2 dt cos2t dt
2 t 12 sin 2t c 2t sin 2t c.
41
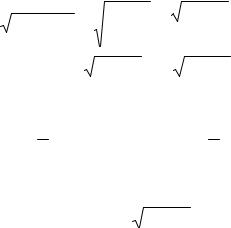
Вернемся к первоначальной переменной интегрирования x. Применяя формулы тригонометрии, получим:
sin t |
x |
, cost |
1 sin 2 t |
|
1 |
x2 |
|
|
|
4 x2 |
. |
||||||
|
|
|
|
|
2 |
||||||||||||
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
sin 2t 2sin t cost 2 |
x |
|
|
|
4 x2 |
|
x |
4 x2 |
|
, |
|||||||
|
|
|
2 |
|
|
|
2 |
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Из равенства sin t 2x получаем t arcsin 2x .
Окончательно имеем:
I5 |
2t sin 2t c 2arcsin |
x |
|
x |
4 x2 |
c. |
|
|
2 |
||||
|
2 |
|
|
|
||
Практическое занятие 6.
Интегрирование функций, содержащих квадратный трехчлен
|
в знаменателе дроби |
||||
Пример1. Найти интеграл |
I1 |
|
|
dx |
|
|
3x 10 |
||||
|
|
x2 |
|||
Решение. Преобразуем квадратный трехчлен ( x2 3x 10 ), а именно – выделим полный квадрат:
x |
2 |
3x 10 |
|
2 |
2 |
3 |
x |
9 |
|
9 |
|
|
|
|
|
3 |
2 |
49 |
|
3 2 |
|
7 |
2 |
|||||
|
= x |
|
2 |
4 |
|
4 |
10 x |
2 |
|
|
4 |
x |
2 |
|
|
2 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тогда получим: I1 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
|
2 |
|
|
7 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применим метод введения под знак дифференциала, а затем свойство инвариантности и табличный интеграл:
42

|
|
|
dx |
|
|
|
|
1 |
|
|
|
x a |
||||
|
|
|
|
|
|
|
ln |
|||||||||
x |
2 |
2 |
|
2a |
x a |
|||||||||||
|
a |
|
|
|
|
|||||||||||
I1 |
|
|
|
|
|
|
dx |
|
|
|
|
|||||
|
|
|
3 |
|
2 |
|
|
7 |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 7 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
d |
x |
2 |
|
|
|
|
|
|
1 |
|
|
x |
|
|
1 |
|
x 2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
2 |
|
2 |
|
c |
ln |
|
c. |
||||
|
3 |
|
2 |
|
7 |
|
2 |
|
|
7 |
x |
3 |
|
7 |
|
7 |
x 5 |
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
x |
2 |
|
|
|
|
2 |
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
dx
 9x2 6x 2
9x2 6x 2
Решение. Выделим полный квадрат в квадратном трехчлене:
9x2 6x 2 ((3x)2 |
2 3x 1 1) 1 2 (3x 1)2 1 |
|||
Тогда получим: |
J2= |
dx |
|
|
2 |
1 |
|||
|
|
3x 1 |
||
Применим метод введения под знак дифференциала, а затем свойство инвариантности и табличный интеграл:
|
|
|
dx |
|
|
|
x2 a2 |
|
c. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ln |
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
2 |
a |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
I2 |
|
|
dx |
1 |
d (3x 1) |
1 ln |
|
3x |
1 3x 1 2 |
1 |
|
c |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
3x 1 2 1 |
3 |
3x 1 2 1 |
|
3 |
|
|
|
|
|
|
||||||||||
|
|
1 ln |
|
|
|
|
|
|
|
|
|||||||||||||
|
3x 1 9x2 |
6x 2 |
c. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 1 |
dx |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. Найти интеграл I3 |
|
|
|
|
|
|
|||||||||||||||||
4x2 |
4x 17 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Найдем производную квадратного трехчлена и запишем ее в числителе, а затем проведем тождественные преобразования в числителе.
|
|
|
|
3x 1 |
|
|
3 |
(8x 4) 3 1 |
|
3 (8x 4) 1 |
|||
I3 |
|
|
|
dx = |
|
8 |
2 |
dx |
|
8 |
2 |
dx |
|
4x2 |
4x 17 |
|
|
4x2 4x 17 |
|
|
|
||||||
|
|
|
|
|
4x2 4x 17 |
||||||||
43
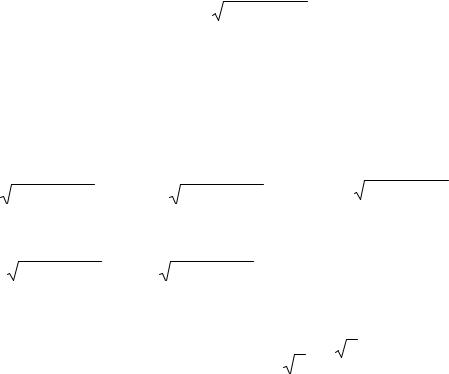
= |
3 |
|
(8x 4)dx |
1 |
|
|
|
dx |
8 |
2 |
4x |
2 |
4x 17 |
||||
|
|
4x 4x 17 2 |
|
|
||||
Для нахождения первого интеграла применим метод введения под знак
дифференциала и табличный интеграл dx |
ln |
|
x |
|
c |
|
|
||||
x |
|
|
|
|
|
|
|
|
|
|
Для нахождения второго интеграла выделим полный квадрат в квадратном трехчлене ( 4x2 4x 17 ), а затем – метод введения под знак дифференциала, свойство инвариантности неопределенного интеграла и табличный интеграл
|
|
dx |
|
|
1 arctg |
x |
|
c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
d (4x2 4x 17) |
1 |
dx |
3 |
|
|
|
|
2 |
|
|
1 |
|
d (2x 1) |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
I3 8 |
|
|
4x2 4x 17 |
2 |
|
8 ln |
|
4x |
|
4x 17 |
|
|
|
|
|
|||||||||||||
|
|
(2x 1)2 16 |
|
4 |
(2x 1)2 42 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 ln |
|
4x2 |
4x 17 |
|
|
1 |
arctg |
2x 1 |
c. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
8 |
|
|
|
|
|
|
16 |
|
4 |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 4. Найти интеграл I4= |
|
|
dx. |
|
|
|
|
|
|
|||||||||||||||||||
3 |
2x x |
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. В числителе подынтегральной дроби выделим производную квадратного трехчлена знаменателя, а затем выполним тождественные преобразования в числителе дроби.
|
|
|
|
x 3 |
|
|
|
|
1 |
( 2x 2) 1 3 |
|
1 |
( 2x 2) 4 |
|
|||
|
|
|
|
|
|
|
2 |
2 |
dx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I4 |
|
|
3 2x x2 |
dx |
|
3 2x x2 |
dx |
|
|
3 2x x2 |
|||||||
|
1 |
|
( 2x 2) |
|
dx 4 |
|
dx |
|
. |
|
|
|
|
|
|||
2 |
3 2x x |
2 |
|
3 2x x |
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для нахождения первого интеграла применим метод введения под знак
дифференциала и табличный интеграл |
dx |
2 |
x c. |
|
x |
||||
|
|
|
44
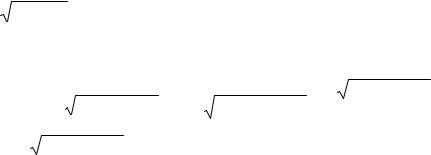
Для нахождения второго интеграла выделим полный квадрат в квадратном трехчлене
3 2x x2 :
3 2x x2 (x2 2x 3) ((x2 2x 1 1) 1 3) 4 (x 1)2 22 (x 1)2 ,
а затем – метод введения под знак дифференциала, свойство инвариантности неопределенного интеграла и табличный интеграл
|
|
|
dx |
|
arcsin |
x |
c. |
|
|
|
|
|
|
|
|
|
||
|
a |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
||||||||
I4 |
|
1 |
d (3 2x x2 ) |
4 |
|
|
d (x 1) |
|
3 2x x2 |
4arcsin |
x 1 |
c |
||||||
2 |
|
3 2x x2 |
|
22 (x 1)2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||||||||
c |
3 2x x2 4arcsin |
x 1 |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
45
