
738
.pdf
Значения c 0, α, β, определяются эмпирическим путем.
В качестве примера приведем квадратичную зависимость молярной теплоемкости азота от температуры:
сP = 29,02 + 0,00531t + 0,000000127 t 2, кДж/(моль∙ К).
В диапазоне температур, имеющих место в современных тепловых машинах, зависимость теплоемкости от температуры с достаточной степнью
точности можно считать линейной. Это значит, что в уравнении (2.34)
можно учитывать только два первых слагаемых, т.е.: |
|
c = c0 +α t |
(2.35) |
Теплоемкость, соответствующую данной температуре, |
называют |
и с т и н н о й. и вычисляют по уравнению (2.34) или (2.35). |
|
В теплотехнических расчетах часто возникает необходимость знать с р е д н е е значение теплоемкости в определенном интервале температур.
|
|
Средней теплоемкостью cср |
данного процесса в интервале температур |
||||||||
|
|
от t1 до t2 называют отношение теплоты процесса q1-2 |
к разности |
||||||||
|
|
температур t2 – t1 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q 1 2 |
|
|||||
|
|
cср = |
|
|
|
|
|
. |
|
|
|
|
|
|
t |
2 |
t |
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
После подстановки значений q1-2 = 2 c dt и с из (2.35), получим: |
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
с с р =с0 |
+ α |
t1 t2 |
. |
(2.36) |
|||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
В Приложении табл.5 приведены значения истинной теплоемкости отдельных газов, а в табл. 6 – их средние значения в диапазоне температур от 0 до 2300 0С. При необходимости вычисления средней теплоемкости в диапазоне температур от t1 до t2 можно применить формулу
|
|
|
|
|
c |
|
|
t2 |
t |
|
c |
|
t1 |
t |
|
|
|
|
сср |
tt |
2 |
|
ср |
|
0 |
|
2 |
|
|
ср |
0 |
|
1 |
. |
(2.37) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
t2 |
t1 |
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Показатель адиабаты к |
|
также зависит от температуры. Это можно по- |
||||||||||||||||
казать, представив соотношение (2.31) в виде |
|
|
|
|
|
|||||||||||||
|
|
|
cp |
|
c R |
1 |
|
R |
|
|||||||||
к = |
|
|
|
|
|
v |
|
|
|
|
|
|
(2.38) |
|||||
|
|
cv |
|
cv |
|
|
cv |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Экспериментальное изучение зависимости |
|
c = f (t) для идеальных га- |
||||||||||||||||
зов показывает, что у каждого газа существует некоторый интервал температур, в котором его теплоемкость практически постоянна.
Идеальный газ в том интервале температур, где теплоемкость не изменяется, называется с о в е р ш е н н ы м..
Соотношения (2.27) и (2.29) справедливы только для совершенного оаза
41
Опытное изучение зависимости теплоемкости газов от давления показывает, что это влияние незначительное, и в практических расчетах его можно не учитывать.
2.2.4 Теплоемкость газовых смесей
В справочной литературе приводятся теплоемкости только для отдельных газов, в то время как при тепловых расчетах приходится встречаться с газовыми смесями. Ниже приведены выражения для вычисления теплоемкости смеси газов, если она задана парциальными давлениями, массовыми или объемными долями.
|
|
n |
cp |
i pi |
|
|||||
сp см = |
|
|
i 1 |
|
|
i |
|
|
|
, |
|
|
см pсм |
|
|||||||
|
|
|
|
|
||||||
cp см = |
|
n |
сp |
gi , |
|
|||||
|
|
|
|
i 1 |
|
|
|
i |
|
|
сp |
см |
n |
|
|
cp |
, ri . |
|
|||
|
|
i 1 |
|
|
i |
|
||||
|
n |
cv i i pi |
|
|||
cv cм = |
i 1 |
|
|
|
. |
|
см |
рсм |
|||||
|
|
|||||
cv cм = n |
|
cvi gi i |
|
|||
|
i 1 |
|
|
|
||
cv см |
n |
|
cv i ri |
|
||
|
i 1 |
|
|
|||
(2.39)
(2.40)
(2.41)
Для смеси газов справедливо уравнение Майера, которое будет иметь
вид
сp см – сv см = R см. |
(2.42) |
2.3. Термодинамические процессы
2.3.1. Понятие термодинамического процесса
Общее представление о состоянии системы и ее изменениях (процессах) изложено в подпункте 1.1.3.
Термодинамический процесс – это определенная последовательность изменения параметров состояния рабочего тела системы.
Термодинамические процессы могут быть равновесными и неравновесными, обратимыми и необратимыми. Если изменение состояния термодинамической системы протекает с нарушением ее внутреннего равновесия, то имеет место неравновесный термодинамический процесс. Реальные процессы, наблюдаемые в природе, в эксперименте, в машинах, являются неравновесными, их описание методами термодинамики невозможно.
С целью изучения основных свойств систем при обмене энергией с окружающей средой используют подход научной абстракции, идеализируют реальные процессы, принимая их за равновесные.
|
|
Термодинамический процесс, протекающий с бесконечно малым |
|
|
|
отклонением |
состояния системы от равновесного, называется |
|
|
р а в н о в е с н ы м. |
|
42 |
|
|
|
Понятие об обратимых и необратимых процессах изложено в подпункте 1.1.5. Ниже рассматриваются только равновесные и обратимые термодинамические процессы идеального совершенного газа.
Для равновесной термодинамической системы связь между термодинамическими параметрами устанавливается уравнением состояния идеального газа (2.9). Следовательно, это уравнение справедливо и для равновесного термодинамического процесса не только в начальном и конечном состояниях системы, но и в любом промежуточном ее состоянии.
Вобщем случае в процессе могут изменяться произвольно (независимо) два термодинамических параметра из трех. Изучение работы тепловых машин показывает, что наибольший интерес для практики представляют конкретные термодинамические процессы, а именно изменения состояния, протекающие при постоянных давлении, объеме, и температуре, а также без теплообмена с окружающей средой. Их характерной особенностью является то, что для совершенного газа величина теплоемкости на всем протяжении процесса остается неизменной.
Втермодинамике широко используются графические методы анализа процессов. При этом удобнее использовать не пространственные трехмерные изображения линий, описываемых функцией f(p,v,T), а их двухмерные проекции на одну из трех координатных плоскостей. Как правило, используется графическое изображение термодинамических процессов в координатах pv
иTs, а в особых случаях – в координатах i s; p i; id и др.
Вpv и Ts – координатах на рис.2.3 и 2.4 показан произвольный термодинамический процесс изменения параметров от состояния 1 до состояния 2.
P |
|
|
|
|
|
|
1 |
|
T |
2 |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
d |
|
|
|
|
|
a |
b |
V |
a |
b |
S |
|
Рис 2.3 |
|
|
Рис. 2.4 |
|
На рис. 2.3 площадь, ограниченная кривой процесса 1-2, осью абсцисс и крайними ординатами a и b , как было показано в 1.2.5, численно равна работе расширения, а площадь, ограниченная кривой процесса, осью ординат и крайними абсциссами c и d, – технической работе.
В Ts - координатах площадь, ограниченная кривой процесса 1-2, осью абсцисс и крайними ординатами а и b, выражается интегралом:
43
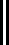
Fа-1-2- б = 12 Tds
2
Поскольку dq = Tds или q = 1 Tds , то Fа-1-2-б численно равна подве-
денной теплоте в процессе.
Так как указанные площади зависят от характера процесса, то теплота и работа являются его функциями.
Независимо от особенностей процесс их анализа проводится в определенной последовательности, заключающейся в следующем:
– устанавливается характер процесса, назначается постоянный пара-
метр;
–с использованием первого закона термодинамики и конкретных особенностей процесса выводится его уравнение;
–из уравнения процесса и уравнения состояния выводятся соотношения между термодинамическими параметрами;
– указывается способ построения графиков в координатах pv и Ts;
–определяется изменение внутренней энергии, энтальпии и энтропии рабочего тела;
–записываются выражения для работы расширения; работы технической и теплоты процесса;
–устанавливается количественное соотношение между теплотой, изменением внутренней энергии и работой в процессе.
Используя указанную последовательность, проведем анализ обобщенного для всех возможных процессов – п о л и т р о п н о г о.
2.3.2. Политропный процесс
Определение процесса
Термодинамический процесс, протекающий при неизменной теплоѐмкости, называется п о л и т р о п н ы м.
Название “политропный” происходит от греческих слов “поли” – много и “тропос” – направление, путь. В политропном процессе в общем случае могут изменяться все термодинамические и калорические параметры кроме теплоѐмкости, которую обозначают через cп.
Вывод уравнения процесса.
Для вывода уравнения используем выражение первого закона термодинамики, записанное через энтальпию и внутреннюю энергию:
dq = di - vdp и dq = du + pdv.
Выразив через теплоемкости записанные выражения, получим:
cп dT = cp dT – vdp и cпdT = cv dT + pdv.
Отсюда
44
|
|
|
|
|
(сп – сp)dT = -vdp |
и (cп –cv)dT = pdv. |
|
|
|||||||||
|
Разделим почленно первое уравнение на второе: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
cп c p |
vdp |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
c |
п |
c |
v |
pdv . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь левая часть равенства определяется только теплоемкостью рабочего |
|||||||||||||||||
|
Разделим почленно первое уравнение на второе: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
cп cp n . |
|
|
|
|
(2.43) |
||
|
|
|
|
|
|
|
|
|
|
cп cv |
|
|
|
|
|
|
|
|
Проведя разделение переменных, |
получим: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
n |
dv dp . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
v |
|
p |
|
|
|
|
|
|
После интегрирования этого соотношения в пределах от начала до кон- |
||||||||||||||||
ца процесса и антилогарифмирования, будем иметь: |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
p1 v1n = p2 v2n. |
|
|
|
|
|
||||
|
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
р vn = const. |
|
|
|
|
(2.44) |
||||
|
Выражение (2.44) |
называется у р а в н е н и е м п о л и т р о п н ог о |
|||||||||||||||
п р о ц е с с а. |
Оно |
устанавливает |
|
|
|
|
|
|
|||||||||
связь |
между |
параметрами |
состоя- |
|
Cn |
|
|
|
|||||||||
(+ |
8 |
) |
|
|
|
||||||||||||
ния |
в |
процессе |
с |
теплоемкостью |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
cn = const. Показатель степени n в |
|
|
|
|
|
|
|||||||||||
уравнении называют |
п о к а з а т е - |
|
Cp |
|
|
|
|||||||||||
л е м |
|
п о л и р о п ы. |
Он прини- |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
мает |
|
для |
|
каждого |
сn конкрет- |
|
C V |
|
|
|
|||||||
ное |
числовое |
|
значение |
и, как |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
изображено на рис.2.5, может ме- |
n (- 8) |
0 |
|
1 |
x |
n (+ 8) |
|||||||||||
няться |
от |
- ∞ до |
+∞. Здесь зависи- |
|
|
|
|
|
|
||||||||
мость |
теплоемкости |
политропного |
|
|
|
|
|
|
|||||||||
процесса от показателя |
n получена |
|
|
|
|
|
|
||||||||||
из (2.43) в виде |
|
|
|
|
|
|
|
|
Cn |
|
|
|
|||||
|
|
|
c n к . |
|
|
|
|
|
|
(- |
8) |
|
|
|
|||
|
|
c |
|
|
(2.45) |
|
|
|
|
|
|
|
|||||
|
|
n |
v |
n -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 |
|
|
||
|
Соотношение между термодинамическими параметрами |
|
|||||||||||||||
|
Используя уравнения (2.9) и (2.44), получим следующие соотношения: |
||||||||||||||||
|
p |
v |
|
n |
|
|
v |
|
p |
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
1 |
|
|
и |
2 |
|
|
1 |
n |
; |
|
|
|
(2.46) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
p1 |
|
|
|
|
|
v1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
v2 |
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|||
|
|
|
T |
|
|
|
|
|
T |
p |
|
|
n |
|
|
|
|||||||||
p |
|
n 1 |
|
2 |
|
|
|||||||||||||||||||
2 |
|
|
|
2 |
|
и |
2 |
|
|
|
|
|
; |
(2.47) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p1 |
T1 |
|
T1 |
|
p1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
v |
|
|
|
|
v |
2 |
T |
n 1 |
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
1 |
|
|
и |
|
|
|
|
|
1 |
|
|
|
|
(2.48) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
T1 |
|
v2 |
|
|
|
|
|
v1 |
T2 |
|
|
|
|
|||||||
Уравнения (2.46) – (2.48) при заданном показателе политропы n и из- |
||||||||||||||||||||||||||
вестном одном из состояний процесса позволяют определить любое другое |
||||||||||||||||||||||||||
состояние, если в нем известен хотя бы один из параметров. |
|
|
|
|
||||||||||||||||||||||
При анализе процессов часто возникают задачи определения показателя |
||||||||||||||||||||||||||
политропы по параметрам двух известных состояний. Выражение для вы- |
||||||||||||||||||||||||||
числения n |
получим из уравнения (2.46) в виде: |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
p |
|
|
|
v T |
|
|
|
|
|
|||
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
n = |
p2 |
= |
ln |
|
p |
2 |
|
|
ln v T |
|
|
|
|
(2.49) |
|||||||||
|
|
|
|
|
v2 |
|
|
|
|
|
|
1 |
2 . |
|
|
|
||||||||||
|
|
|
|
|
|
|
ln |
|
|
ln |
p T |
2 |
|
ln |
v |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
v1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
p2T1 |
|
|
|
v1 |
|
|
|
|
|
|||||
Графическое изображение процесса |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Графическое изображение политропного процесса в координатах pv |
||||||||||||||||||||||||||
или Ts называется п о л и т р о п о й, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Построение кривой процесса в координатах |
|
pv проводится с исполь- |
||||||||||||||||||||||||
зованием уравнения (2.46), записанного в виде: |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
p v n |
1 |
|
, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
1 |
|
vi n |
|
|
|
|
|
|
|
|
|
|
где pi |
и vi – текущие значения давления и удельного объема; |
|
|
|
|
|||||||||||||||||||||
p1 |
и v1 – |
исходные значения указанных параметров. |
|
|
|
|
||||||||||||||||||||
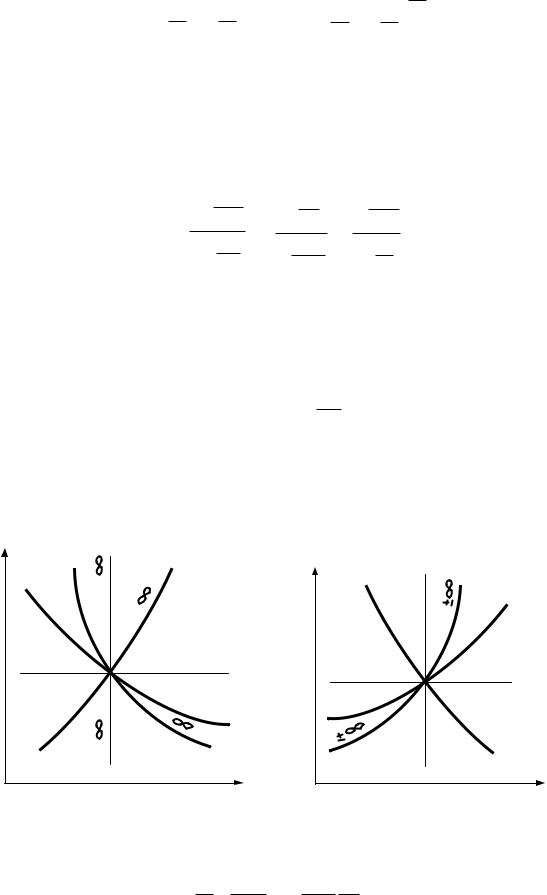
На рис. 2.6 изображены некоторые политропные процессы в pv - коор- |
||||||||||||||||||||||||||
динатах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
V |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n= - |
V |
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
n=k |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
n=1 |
|
|
|
|
|
n=1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
n=1 |
|
|
|
|
|
|
|
n= |
|
|
|
1 |
V |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
V n |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
V |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||
|
|
n=+ |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n=k |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.7 |
|
|
|
|
Для построения процесса в координатах |
|
Ts, рис. 2.7, |
|
|
используют |
|||||||||||||||||||||
уравнение второго закона термодинамики, так |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
ds dq |
cn dT |
cv |
n к dT . |
|
|
|
|
|
|
|
(2.50) |
||||||||||
|
|
|
|
|
|
|
T |
|
|
T |
|
|
|
n - 1 |
|
T |
|
|
|
|
|
|
|
|
||
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связь параметров начального состояния с текущим получим путем интегрирования выражения (2.50) в пределах от 1 до i,
|
n к |
T |
|
||
si = s1 + cv |
|
ln |
|
. |
(2.51) |
n 1 |
T |
||||
|
|
|
1 |
|
|
Справедливы и следующие выражения: |
|
||||
si = s1 + cpln Ti /T1 – R ln pi /p1 |
и si = s1 + cvln Ti /T1 + R ln vi /v1 . |
|
|||
Работа процесса.
Используя уравнение политропы, выразим работу расширения (1.9) через начальные и конечные параметры процесса
2 |
2 |
n |
2 |
|
|
lрасш = pdv p1 |
v 1 |
dv p1v1n |
dv |
. |
|
n |
n |
||||
1 |
1 |
v |
1 |
v |
|
|
|
|
|||
После интегрирования и некоторых преобразований получим:
|
1 |
|
( p1v1 p2 v2 ) = |
RT |
|
|
|
|
T |
|
|
lрасш = |
|
|
1 |
|
1 |
|
2 |
. |
|||
n 1 |
|||||||||||
n |
1 |
T |
|||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
Заменив отношение температур отношением давлений, будем иметь:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
p |
2 |
|
|
n |
|
|
|
|
|||
l |
|
|
|
= |
|
|
RT |
1 |
|
|
|
|
|
|
. |
(2.52) |
|||||||||||
|
|
|
n 1 |
|
|
|
|
|
|||||||||||||||||||
|
|
расш |
|
|
1 |
|
|
|
|
p |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проводя те же операции, что и при выводе lрасш |
получим уравнение |
||||||||||||||||||||||||||
для технической работы в виде |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
T |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
= - |
|
vdp |
|
|
|
RT |
1 |
2 |
|
|
|
|||||||||||||
|
|
n |
|
|
|
|
|
||||||||||||||||||||
|
тех |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
T |
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
n 1 |
|
|
|||||||||
lтех = |
|
|
n |
|
|
|
|
|
|
|
n |
|
|
. |
(2.53) |
||||||||||||
|
|
|
|
|
RT |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n 1 |
1 |
|
|
p |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сравнивая выражения (2.52) и (2.53), видим, что техническая работа в n раз больше работы расширения, т.е.
lтех = n lрасш.
Теплота процесса.
Теплоту политропного процесса выражают через теплоемкость, либо используют для этого выражение первого закона термодинамики:
q = cп (Т2 – Т1) = cv |
n к |
T T |
|
, |
||||||
|
|
1 |
||||||||
|
|
n 1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
q = ∆u + lрасш = cv (Т2 |
– Т1) - |
|
R |
|
T2 T1 , |
|||||
n |
|
|
||||||||
|
|
|
|
|
1 |
|
|
|||
q = i + lmex = cp (T2 – T1) - |
|
|
n |
|
R (T2 – T1 ). |
|||||
|
|
|||||||||
|
n 1 |
|||||||||
47
Соотношение между теплотой, работой и внутренней энергией.
Для оценки доли теплоты, затраченной на изменение внутренней энергии, в термодинамике при исследовании циклов вводят коэффициент α , которым обозначают отношение
α = |
u |
. |
(2.54) |
|
|||
|
q |
|
|
Долю тепла, расходуемую на совершение работы расширения, обозначают через , тогда
|
l |
расш |
или |
1 . |
(2.55) |
|
q |
||||
|
|
|
|
|
Выразив изменение внутренней энергии и теплоту через теплоемкости, получим:
|
u |
|
cv T |
|
n 1 |
|
1 |
1 к |
|
α = |
|
|
|
и |
|
. |
|||
|
c T |
n к |
|||||||
q |
n к |
||||||||
|
|
|
п |
|
|
|
|
|
|
Таким образом, распределение теплоты между внутренней энергией и работой в процессе можно оценить по известному показателю политропы.
Втеплотехнике часто используются так называемые и з о п а р а м е т-
ри ч е с к и е процессы: изобарный, изохорный, изотермический и адиабатный.
2.3.3. Изобарный процесс
Процесс, протекающий при постоянном давлении, называют и з о- б а р н ы м.
Уравнение процесса записывается в виде p = const или cn = cp.
Из уравнения политропы следует, что для изобарного процесса n = 0. Соотношение параметров в начальном и конечном состояниях процесса устанавливается с использованием уравнений состояния, записанных для этих точек: p1v1 = RT1 и p2v2 = RT2. Поделив одно уравнение на другое, получим:
v1 |
|
T1 |
. |
|
|
||
v2 |
|
T 2 |
|
В изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам.
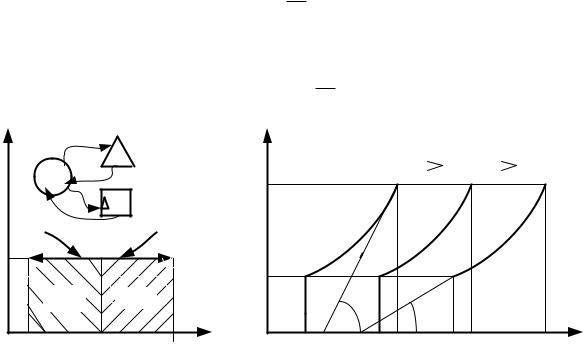
График процесса называется и з о б а р о й. В pv–координатах (рис.2.8) изобара – прямая линия, параллельная оси удельных объемов. В координатах Ts изобара – логарифмическая кривая (рис.2.9), так как она описывается уравнением, полученным из (2.51) при n = 0:
|
Ti |
|
|
si = s1 + cp ln |
|
. |
(2.56) |
T |
|||
1 |
|
|
|
48
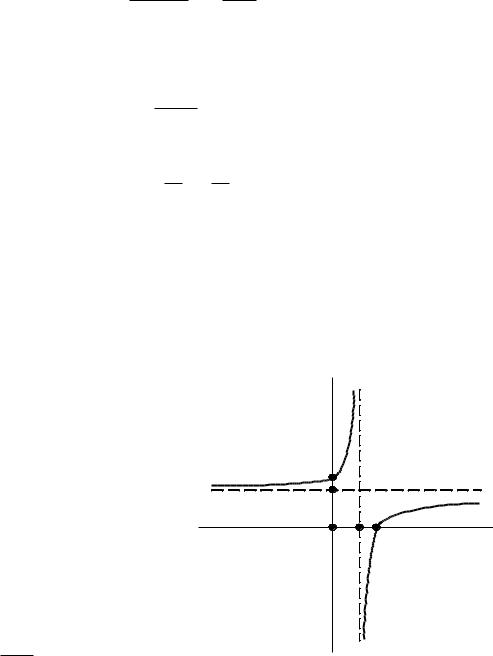
|
Крутизна |
изобары в Ts-координатах для каждой температуры опре- |
|||||||
деляется тангенсом угла наклона кривой к оси абсцисс, т.е. |
|
||||||||
|
|
|
|
|
tg β = dT .. |
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
Принимая во внимание, |
что |
для изобарного процесса справедливы |
|||||||
уравнения |
dq = T ds и |
dq = cp dT, |
получим: |
|
|
|
|||
|
|
|
|
|
tg β = T . |
|
|
(2.57) |
|
|
|
|
|
|
|
c p |
|
|
|
p |
|
|
|
|
T |
|
|
|
|
|
|
|
lр |
|
|
|
|
|
|
|
|
|
|
|
|
p |
P* |
P** |
|
|
q |
|
|
|
|
|
|||
|
|
|
|
T2 |
|
2 o |
o |
o |
|
|
|
|
|
|
|
||||
|
|
|
u |
|
|
|
|
2* |
2** |
|
|
|
|
|
|
|
|
|
|
|
-q |
|
+q |
|
|
|
|
|
|
2 |
2* |
1 |
|
2 |
|
|
|
|
|
=p |
|
|
|
|
|
|
|||
о |
о |
о |
|
|
|
|
|
|
|
p1 |
|
T1 |
1 |
1* |
1** |
|
|||
|
|
|
|
|
|||||
|
|
|
lрасш |
|
|
o |
o |
o |
|
|
lсжlc |
|
|
|
|
|
|
||
|
lрасш |
|
|
|
|
|
|
||
|
|
ж |
|
|
|
|
** |
|
|
|
|
|
|
|
|
|
|
||
|
V* |
v1 |
v2 v |
|
a |
c b |
e d |
f s |
|
|
|
Рис. 2.8 |
|
|
|
|
Рис. 2.9 |
|
|
Отсюда следует, что с увеличением температуры и уменьшением теплоемкости крутизна изобары растет. Подкасательная к изобаре в любой точке определяет значение истинной теплоемкости cp при температуре T .
Все изобары являются эквидистантными кривыми (на рис.2.9 изобары при р, р* и р**), так как при одной и той же температуре они имеют одинаковые угловые коэффициенты. Кроме того, расстояние между двумя изобарами вдоль оси абсцисс при разных температурах одинаково. Так при температуре T1 отрезок ce между изобарами р* и р** определяется выражением:
|
з** c dT vdp |
|
|
|
p** |
|||||
sce |
з* |
v |
|
|
R ln |
|
|
. |
||
T |
|
|
p |
* |
||||||
|
|
|
|
|
|
|
|
|
||
Аналогично найдем отрезок d f |
межу теми же изобарами при темпера- |
|||||||||
туре Т2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
** |
|
|
|
|
|
|
|
sd f |
R ln |
p |
. |
|
|
|
||
|
|
* |
|
|
|
|||||
|
|
|
|
|
|
p |
|
|
|
|
В итоге получили |
sce sd f или |
c e = d f. |
|
|
|
|||||
Изменение внутренней энергии запишем через теплоемкость при постоянном давлении, используя для этой цели уравнение Майера:
∆u = (cp – R) (T2 – T1).
Изменение энтальпии в процессе вычисляется как
∆i = cp(T2 - T1).
Приращение энтропии можно записать и через cp, и через cv:
49
s2 – s1= cp ln (T2/T1) и
Работа расширения выражается
s2 – s1 = cv ln (T2/T1) + R ln (v2 /v1).
следующим образом:
lрасш = 12 pdv p(v2 v1) R(T2 T1) .
При изменении температуры на один градус работа расширения численно равна величине газовой постоянной.
Техническая работа будет равна нулю, так как dp = 0:
lтех = - 12 vdp 0 .
Количество теплоты, сообщаемое газу в изобарном процессе, вычисляется по уравнению:
q = cp (Т2 – Т1) = i2 – i1.
Часть сообщенной теплоты идет на изменение внутренней энергии, а другая часть – на работу расширения.
u |
|
cv T2 T1 |
|
|
1 |
|
|
l |
расш |
1 |
к 1 |
|||
α = q |
|
|
|
|
|
, |
|
|
|
. |
||||
c |
T T |
|
к |
|
|
|||||||||
|
|
q |
к |
|||||||||||
|
|
p |
2 1 |
|
|
|
|
|
|
|
|
|
|
|
2.3.4. Изохорный процесс
Процесс, протекающий при постоянном объеме, называется и з о х о р н ы м.
Уравнение процесса записывается в виде v = const или cn = cv. Показатель политропы для изохорного процесса получим из уравнения
политропы, если раскроем его относительно удельного объема:
|
n |
const |
const* |
||
v = |
|
p |
|
1 . |
|
|
|
|
|
|
|
|
|
p n |
|||
|
|
|
|||
Из этого следует, что удельный объем может быть постоянным только при показателе политропы, равном n= ±∞.
Из уравнения состояния при v=const получим связь между параметрами в конечных точках процесса:
p2 T2 . p1 T1
Это значит, что при постоянном объеме давление газа изменяется прямо пропорционально изменению абсолютной температуры.
График процесса называется и з о х о р о й. В pv–координатах (рис.2.10) изохора – прямая линия, параллельная оси давлений. В координатах Ts изохора (рис.2.11) – логарифмическая кривая, так как текущие значения энтропии и температуры связаны уравнением:
|
= |
i dq |
|
i c |
dT |
cv ln |
T |
|
|||
si - s1 |
|
|
|
v |
|
i |
. |
(2.58) |
|||
|
T |
|
T |
|
|||||||
|
1 |
|
1 |
|
|
T |
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
50
