
738
.pdf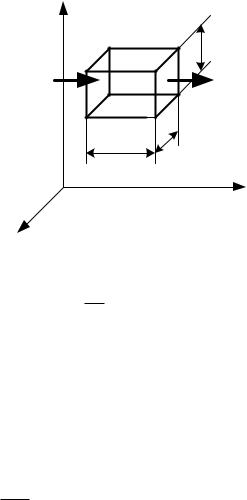
(рис.6.2), который расположен так, что его грани параллельны соответству- |
|||||||||||||
ющим координатным плоскостям. С целью упрощения вывода уравнения |
|||||||||||||
предположим, что имеется одномерное (в направлении оси |
x ) температур- |
||||||||||||
ное поле и что теплофизические свойства тела не зависят от координат и |
|||||||||||||
времени. |
|
|
|
|
|
|
|
|
|
|
|
||
|
При выводе уравнения используется |
|
|
|
|
|
|
||||||
закон сохранения энергии, который для |
|
|
|
|
|
|
|||||||
рассматриваемого случая |
устанавливает, |
y |
|
|
|
|
|
||||||
что |
количество |
теплоты, |
подведенное к |
|
|
|
|
|
dy |
||||
элементарному |
объему за время |
d , |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
равно изменению его энтальпии. |
|
qx |
|
|
|
|
qx+dx |
||||||
|
В |
|
выделенный |
объем |
через |
|
|
|
|
||||
|
|
|
|
|
|
|
z |
||||||
грань с |
координатой x |
за время |
d |
|
|
|
dx |
d |
|||||
проходит |
qx dy |
dz d |
теплоты. |
Через |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
противоположную грань от тела будет от- |
|
|
|
|
|
|
|||||||
водиться |
q x+dx |
dy dz d |
теплоты. Раз- |
|
|
|
|
|
x |
||||
ность этой энергии аккумулируется дан- |
z |
|
|
|
|||||||||
|
|
|
|
||||||||||
ным элементарным объемом. Следова- |
|
|
|
|
|
|
|||||||
тельно, можно записать: |
|
|
|
|
|
Рис. 6.2 |
|
||||||
|
|
|
|
|
- |
|
|
|
|
T |
, |
|
(6.6) |
|
|
|
q x dy dz d |
q x+dx dy dz d = dx dy dz cр |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
ρ |
– |
плотность; |
|
|
|
|
|
|
|
|
|
|
|
cр |
– |
массовая теплоемкость при постоянном объеме; |
|
|
||||||||
|
Т |
– частная производная температуры по времени. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
является неизвестной функцией координаты x. Раз- |
||||||||||
|
q x+dх |
||||||||||||
ложим ее в ряд Тейлора и ограничимся двумя первыми членами ряда, в итоге |
|||||||||||||
будем иметь: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
qx dx. |
. |
|
|
|
|
|
|
|
|
|
|
q x+dx = q x |
+ x |
|
|
|
|
||
С учетом полученного выражения равенство (6.6) приобретает вид:
|
|
|
T |
|
|
|
qx |
dx dy dz d dx dy dz c |
|
d . |
|
|
p |
||||
|
x |
|
|||
После сокращения и подстановки выражения (6.5), записанного для одномерного температурного поля, получим:
сp |
T |
|
2T |
или |
T |
a |
2T |
. |
(6.7) |
|
|
x2 |
|
||||||||
|
||||||||||
|
|
|
|
x2 |
|
|||||
Для выделенного параллелепипеда, имеющего трехмерное температурное поле, необходимо провести аналогичные операции вдоль осей y и z.
В итоге трехмерное температурное поле будет описываться дифференциальным уравнением вида:
111
T |
|
2T |
|
2T |
|
2T |
|
||||
|
a |
|
2 |
|
2 |
|
2 |
. |
(6.8) |
||
|
|
x |
|
y |
|
z |
|
||||
|
|
|
|
|
|
|
|
||||
Уравнение (6.8) называется д и ф ф е р е н ц и а л ь н ы м у р а в н е - н и е м т е п л о п р о в о д н о с т и для трехмерного нестационарного температурного поля. Оно устанавливает связь между временными и пространственными изменениями температуры в любой точке тела.
Величину a |
|
|
|
называют коэффициентом т е м п е р а т у р о - |
|
|
||
|
c p |
|
п р в о д н о с т и . Коэффициент температуропроводности характеризует физическое свойство вещества и имеет единицу м2/с. В нестационарных тепловых процессах а устанавливает скорость распространения изотермических поверхностей. Чем больше коэффициент температуропроводности, тем интенсивнее изменяется температура в теле. Численное значение а определяют химический состав и состояние вещества, а также температура. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы прогреваются быстрее, так как они имеют большее значение а . Определяют коэффициент температуропроводности экспериментальным путем, его значения для материалов приводятся в теплотехнических справочниках.
Полученное дифференциальное уравнение описывает процесс изменения температуры в системе в самом общем виде. При интегрировании его возможно бесчисленное множество решений, удовлетворяющих этому уравнению. Чтобы получить из множества решений одно частное, надо знать особенности явления, т.е. иметь дополнительные сведения о нем.
Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называют у с л о - в и я м и о д н о з н а ч н о с т и .
Условия однозначности включают:
–геометрические условия, характеризующие форму и размер тела или системы;
–физические условия, которыми обладают тела данной системы (плотность, теплоемкость и т.д.);
–граничные условия, которые характеризуют взаимодействие системы с окружающей средой, т.е. условия протекания процесса на границе тела;
–временные условия, характеризующие протекание процесса в начальный момент времени.
Дифференциальное уравнение и приведенные четыре условия однозначности определяют конкретное единичное явление.
Граничные условия могут быть заданы четырьмя способами.
Граничное условие п е р в о г о (I) р о д а . При этом условии считается известной температура на поверхности тела в любой момент времени;
112
Граничное условие в т о р о г о (II) р о д а . Здесь задается для любого времени значение плотности теплового потока в каждой точке поверхности тела;
Граничное условие т р е т ь е г о (III) р о д а . В этих условиях известны температура теплоносителя (окружающей тело среды) –Tm и коэф-
фициента теплоотдачи α |
между поверхностью тела и теплоносителем. Гра- |
||
ничное условие третьего рода записывается так: |
|||
|
T T |
|
T |
|
|
. |
|
|
m cm |
|
|
|
|
|
n ст |
Граничное условие |
ч е т в е р т о г о |
(IY) р о д а предполагает |
|
наличие процесса теплообмена тела с окружающей средой по закону теплопроводности. Считается, что между телами имеется идеальный контакт и температуры соприкасаемых поверхностей одинаковы. В этом случае имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения, т.е.
|
|
T |
|
|
|
|
T |
|
|
|
2 |
|
|
|
|||
1 |
|
|
|
|
|
. |
||
|
|
n ст 1 |
|
|
|
|
n |
ст 2 |
6.3. Стационарная теплопроводность
6.3.1. Теплопроводность однослойной плоской стенки
Исходным уравнением для анализа стационарной теплопроводности плоской однослойной стенки является дифференциальное уравнение (6.8):
T |
|
2T |
|
2T |
|
2T |
|
|||
|
a |
|
|
|
|
|
|
|
|
. |
|
|
2 |
|
2 |
|
2 |
||||
n |
|
x |
|
y |
|
z |
|
|||
|
|
|
|
|
|
|
||||
Для решения поставленной задачи данное уравнение необходимо дополнить условиями однозначности.
Геометрические условия
Задана плоская стенка толщиной δ, рис. 6.3. Плоской называют стенку, которая имеет бесконечно большие длину и ширину по сравнению с толщиной. При этом условии температура по y и z постоянна.
Физические условия
Принимаем коэффициент теплопроводности материала стенки независимым от температуры, т.е. постоянным по ее толщине: λ = const.
Временные условия
Температура любой точки стенки не меняется во времени, тогда
∂Т/∂η = 0.
Граничные условия
Для решения данной задачи используем граничные условия I рода, т.е.
при x = 0, T = Tcm 1 ; при x = δ, T = Tcm 2.
113
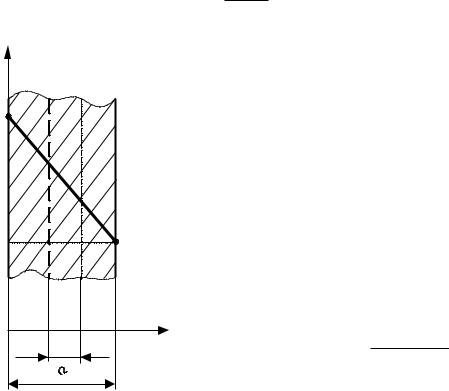
Необходимо определить характер изменения температуры в плоской стенке, т.е. T=f(x) и получить формулу плотности теплового потока.
Исходное уравнение (6.8) при условиях однозначности будет иметьследующий вид:
|
2T |
0 |
|
|
(6.9) |
||
|
x2 |
|
|
|
|
||
|
Первое интегрирование уравнения (6.9) дает |
||||||
T |
|
|
T |
C1 . |
|
||
|
|
|
x |
|
|
|
|
Тст.1 |
|
После второго интегрирования получим: |
|||||
|
|
|
T = C1 x +C2 |
(6.10) |
|||
|
|
Здесь C1 и C2 – постоянные, которые |
|||||
|
определяются из граничных условий. Так, при |
||||||
|
x = 0, |
T = Tcm 1 постоянная |
C2 = Tcm 1 ; |
при |
|||
|
x = δ, |
T = Tcm 2, отсюда |
C1 = (Tcm 2 – Tcm 1) / δ . |
||||
Тст.2 |
|
Подставляя значения постоянных |
С1 и |
||||
|
С2 в выражение (6.10), получим уравнение, |
||||||
|
устанавливающее изменение температуры по |
||||||
|
толщине плоской стенки для случая Tcm 1>Tcm 2: |
||||||
dx |
x |
|
T Tcm 1 Tcm 1 |
Tcm 2 x |
(6.11) |
||
|
|
|
|
|
|
|
|
o |
|
Из уравнения (6.11) следует, что при по- |
|||||
|
стоянном |
коэффициенте |
теплопроводности |
||||
Рис. 6.3 |
температура в стенке изменяется по линейному |
||||||
закону; в координатах |
T x |
она изобразится |
|||||
|
|||||||
прямой линией от Tcm 1 до Тcm 2 , (см. рис 6.3).
Для определения плотности теплового потока, проходящего через стенку в направлении оси x, воспользуемся законом Фурье, согласно которому
|
|
|
T |
|
|
|
q |
x . |
|
||
Заменим ∂Т/∂x значением С1, |
получим: |
|
|
||
|
|
Tcm 1 T cm |
2 . |
(6.12) |
|
q |
|
||||
|
|
|
|
|
|
Анализ уравнения (6.12) показывает, что количество тепла, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности и разности температур на наружных поверхностях стенки и обратно пропорционально толщине стенки.
Разность температур (Тст1 - Tcm2) принято называть т е м п е р а- а т у р н ы м н а п о р о м . Отношение λ / δ н а з ы в а ю т т е п л о - в о й п р о в о д и м о с т ь ю , а обратную ей величину δ/λ – т е р - м и ч е с к и м с о п р о т и в л е н и е м .
114
Используя уравнения (6.11) и (6.12), получим выражение:
T Tcm 1 |
|
q |
x , |
(6.13) |
|
|
|||||
|
|
|
|
которое устанавливает характер распределения температуры по толщине стенки при известных граничных условиях I и II рода.
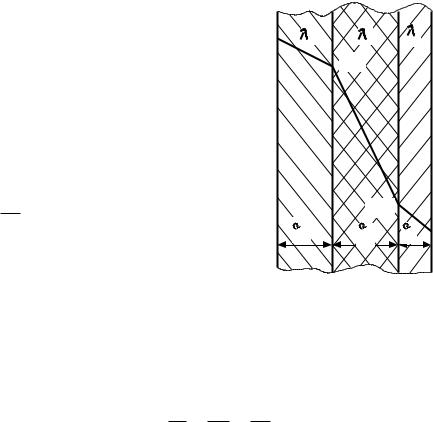
6.3.2.Теплопроводность плоской многослойной стенки
Втеплонапряженных конструкциях энергетических установок часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов и различной толщины. Получим уравнение плотности теплового потока через многослойную стенку, полагая контакт между слоями настолько плотным, что температура на соприкасающихся поверхностях двух смежных слоев одинакова.
Характерной особенностью распространения теплоты при стационарном режиме является то, что плотность теплового потока не зависит от коор-
динаты, т.е. величина q для любого слоя стенки одна и та же.
Решение поставленной задачи рассмотрим на примере трехслойной плоской стенки (рис. 5.5).
Уравнения плотности теплового пото- |
|
|
Тст.1 |
|
|
|
|
|
||||||||||||
ка для каждого слоя стенки запишем анало- |
|
|
1 |
|
2 |
|
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
гично выражению (6.12) в виде системы: |
|
|
|
|
|
|
|
|
Тст.2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tcm 1 Tcm 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Tcm 2 Tcm 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 Tcm 3 Tcm 4 |
|
|
|
|
|
|
|
|
|
|
|
|
Тст.3 |
|||||
q |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
o 1 |
o2 |
|
o3 Тст.4 |
||
Из этих уравнений определим темпе- |
|
|
|
|
|
|
|
|
|
|||||||||||
ратурные напоры в каждом слое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.4 |
|||
Tcm 1 Tcm 2 q |
1 |
, |
Tcm 2 |
Tcm 3 |
q |
2 |
|
|
и |
|
|
Tcm 3 Tcm 4 |
|
3 |
. |
|||||
|
|
|
|
|
|
q |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
Сложив, левые и правые части этих равенств, получим: |
|
|
|
|||||||||||||||||
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|||||
|
|
|
|
cm 1 |
cm 4 |
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или
115
|
q |
Tcm 1 Tcm 4 |
|
|
|
|
||||||||
|
1 |
|
2 |
|
3 |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|||
Для многослойной стенки, состоящей из |
n |
слоев, формула плотно- |
||||||||||||
сти теплового потока будет иметь вид: |
|
|
|
|
|
|
|
|
|
|||||
|
q |
Tcm 1 Tcm n 1 |
|
|
|
(6.14) |
||||||||
|
|
i n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i |
|
|
|
|
|
|||
|
|
|
|
i 1 |
|
i |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для многослойной стенки с различными коэффициентами теплопро- |
||||||||||||||
водности слоев температурный график представляет собой ломаную линию, |
||||||||||||||
(см. рис. 6.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вычисления теплового потока через однослойную цилиндриче- |
||||||||||||||
скую стенку (например, трубу) используется следующее уравнение: |
|
|||||||||||||
|
|
l Tcm 1 |
Tcm 2 |
, |
|
|
(6.15) |
|||||||
Q |
|
1 |
|
|
|
|
d2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 ln d |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
где l – длина трубы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 и d2 – внутренний и наружный диаметры трубы. |
|
|||||||||||||
6.4 Понятие о решении задач нестационарной теплопроводности |
||||||||||||||
Тепловые процессы называются нестационарными, если температур- |
||||||||||||||
ное поле системы, в которой протекает теплообмен, изменяется по |
||||||||||||||
времени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нестационарные процессы теплопроводности имеют место в теплона- |
||||||||||||||
пряженных элементах тепловых машин при их запуске, выключении или при |
||||||||||||||
изменении режима работы. Кроме того, нестацио- |
|
|
||||||||||||
нарная теплопроводность характерна для |
соору- |
T |
|
|||||||||||
жений незащищенного грунта при суточном изме- |
|
|||||||||||||
Tср |
|
|||||||||||||
нении температуры, для большего количества тех- |
|
|||||||||||||
|
|
|||||||||||||
нологических процессов и многих теплообменных |
|
|
||||||||||||
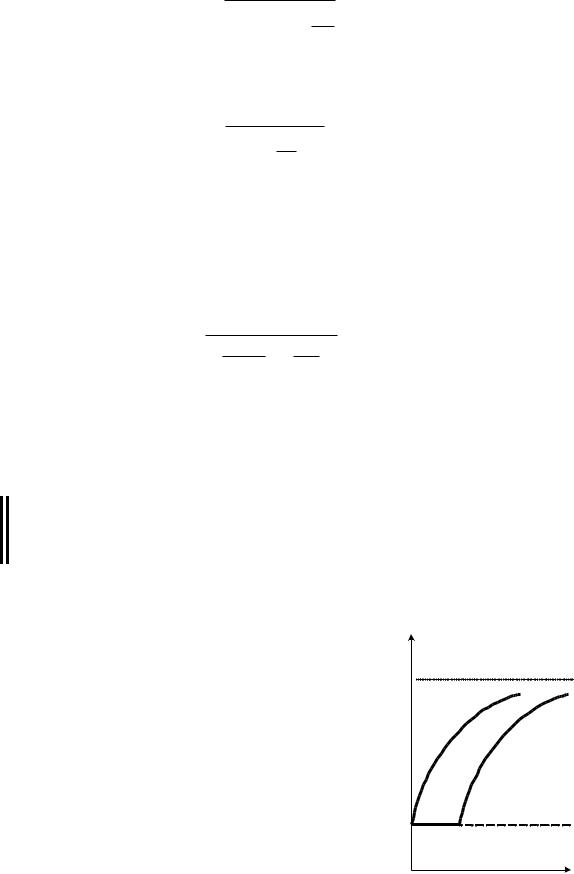
устройств. На рис.6.5 показан временной характер |
1 |
|
||||||||||||
изменения температур двух точек твердого тела, |
2 |
|
||||||||||||
нагреваемого в среде с постоянной температурой |
|
|||||||||||||
|
|
|||||||||||||
Тср. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По мере прогрева тела температура в каждой |
T0 |
|
||||||||||||
точке асимптотически приближается к температу- |
|
|
||||||||||||
ре нагревающей среды. Наиболее быстро изменя- |
|
|
||||||||||||
ется температура точек поверхности |
|
(кривая 1). |
0 |
|
||||||||||
Точки, лежащие внутри тела (кривая 2), будут |
Рис. 6.5 |
|||||||||||||
|
||||||||||||||
|
|
|||||||||||||
116 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прогреваться с некоторым запаздыванием.
Решить задачу нестационарной теплопроводности – значит найти для заданной точки тела величину температуры и количество теплоты в искомый момент времени. Исходными уравнениями задачи нестационарной тепло-
проводности являются дифференциальное |
уравнение (6.8) |
|||||||||
T |
|
2T |
|
2T |
|
2T |
|
|||
|
a |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
||||
|
|
x |
|
y |
|
z |
|
|||
|
|
|
|
|
|
|
||||
и условия однозначности, заданные в виде: |
|
|
|
|
–теплофизических свойств тела , , |
cp ; |
|
|
|
– формы и геометрических размеров тела |
Ф, l ; |
|
||
– температуры тела в начальный момент времени при |
|
|||
Тс т= Т0= f (xст, yст, zcn, ); |
|
|
|
|
|
|
dT |
||
– граничных условий III рода (TСТ |
Т |
ср ) |
|
|
|
||||
|
|
dx ст |
||
= 0
.
Дифференциальное уравнение и условия однозначности дают законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции
T=f(x, y, z, , , cp, , ,T0 ,Т срФ, l) ,
которая удовлетворяла бы исходному уравнению и условиям однозначности.
Отсюда видно, что температура зависит в общем виде от большого числа переменных и постоянных параметров, и определение ее представляет сложную математическую задачу. В зависимости от условий однозначности и требуемой точности разработаны и используются различные методы решения, которые можно разделить на следующие группы:
–аналитические методы;
–численные методы;
–методы аналогий.
Каналитическим методам отнесем решения задач нестационарной теплопроводности, не требующие машинной или аналогичной ей техники. Некоторые из этих методов изложены, например, в [4, 7].
В настоящее время наиболее распространены численные методы решения задач нестационарной теплопроводности. Постановка задач, используемые программы, алгоритмы решений приводятся в ряде работ, например,
в[4, 6.7].
117

Глава 7 Конвективный теплообмен
7.1. Теплоотдача
7.1.1. Основной закон теплоотдачи
Понятие конвективного теплообмена охватывает процесс переноса теплоты конвекцией между твердыми поверхностями и омывающими их теплоносителями. Теплоносителем, как правило, является либо жидкость, либо газ. Однако в качестве теплоносителей могут использоваться двухили трехфазные системы: газ – жидкость; газ – твердые частицы; газ – жидкость
–твердые частицы.
Втеплоносителе с неоднородным полем температур при вынужденном или естественном перемещении макроскопических элементов наряду с конвекцией происходит процесс переноса тепла теплопроводностью.
Совместный процесс конвекции и теплопроводности называют к о н в е к т и в н ы м т е п л о о б м е н о м .
Конвективный теплообмен протекает как внутри теплоносителя, так и на границах его соприкосновения с поверхностями обтекаемых тел.
Конвективный теплообмен между теплоносителем и поверхностью обтекаемого им тела называют т е п л о о т д а ч е й .
Обычно в инженерной практике исследуют теплоотдачу, конвективный же теплообмен внутри теплоносителя при этом не рассматривается.
Тепловой поток при теплоотдаче всегда направлен в сторону меньшей температуры. В процессе теплоотдачи плотность теплового потока, согласно закону Ньютона, прямо пропорциональна температурному напору между
теплоносителем и поверхностью теплообмена, т.е. |
|
q T, |
(7.1) |
где α – коэффициент пропорциональности, называемый к о э ф ф и ц и е
н- |
|
т о м т е п л о о т д а ч и; |
|
∆Т – температурный напор. |
|
При Tm >Tcm это ∆T = Tm - Tcm ; если Tc m> Tm, то |
∆T = Tcm - Tm . |
Здесь индексом m обозначена температура теплоносителя, индексом cm |
|
– температура поверхности теплообмена (стенки). |
|
Для произвольной поверхности при Tm > Tcm |
закон Ньютона запишет- |
ся в виде: |
|
|
Tcm |
.F . |
(7.2) |
Q Tm |
|||
Значения F, Tm и Tcm в уравнении (6.2) не отражают условий теплооб- |
|||
мена, влияющих на величину Q . Здесь |
α не является физической посто- |
||
|
|
|
|
118 |
|
|
|

янной, присущей данному теплоносителю, а зависит от множества факторов, формирующих картину течения около стенки. По этой причине простота уравнения (7.1) представляется кажущейся, и особенности его использования заключаются в сложности определения коэффициента теплоотдачи.
7.1.2. Факторы, влияющие на коэффициент теплоотдачи.
Величина коэффициента теплоотдачи характеризует интенсивность конвективного теплообмена на границе “теплоноситель-стенка”.
Численно коэффициент теплоотдачи равен тепловому потоку, приходящемуся на единицу поверхности при температурном напоре, равный единице, т.е.
Q .
F T
Отсюда же следует и единица α – Вт/(м2 К).
Коэффициент теплоотдачи имеет весьма широкий диапазон численных значений, табл. 7.1.
|
|
Таблица 7.1 |
||
Особенности теплоотдачи |
, |
вm / м2 К |
. |
|
Естественная конвекция газов |
|
6…40 |
|
|
Вынужденное движение газов |
|
12…120 |
|
|
Вынужденное движение пара в трубах |
110…2200 |
|
|
|
Естественная конвекция воды |
110…1100 |
|
|
|
Вынужденное движение воды |
500…11000 |
|
|
|
Пузырьковое кипение воды |
8500…18000 |
|
||
Конденсация водяного пара |
4500…22000 |
|
||
На величину коэффициента теплоотдачи влияют, прежде всего, теплофизические свойства теплоносителя, его фазовое состояние, вид движения
(естественное или вынужденное) |
и р е ж и м т е ч |
е н и я теплоносителя. |
Различают л а м и н а р н ы й , |
п е р е х о д н ы й |
и т у р б у л е н т - |
н ы й режимы течения. |
|
|
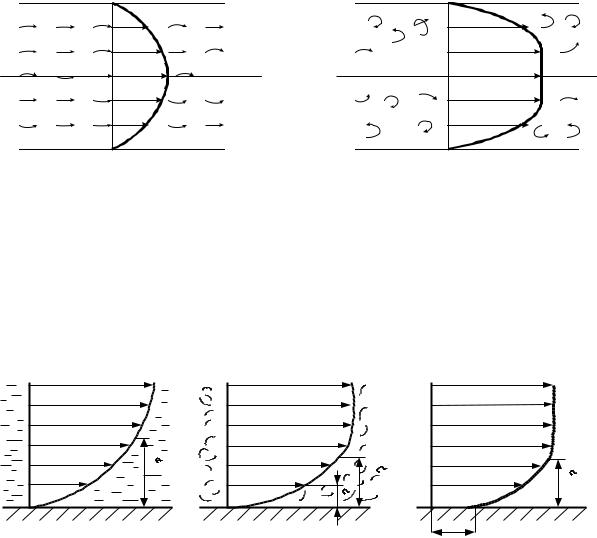
При ламинарном (слоистом) режиме макрочастицы жидкости движутся, не перемешиваясь, параллельно омываемым стенкам и траекториям других частиц. В силу внутреннего трения скорость теплоносителя переменна по сечению нормальному к поверхности. Так, для канала круглого сечения эпюра скорости имеет параболическую форму, рис.7.1, а Перенос тепла при ламинарном режиме движения происходит в осноном за счет теплопроводности теплоносителя и естественной конвекции.
При турбулентном режиме макрочастицы перемещаются по сложным траекториям, не совпадающим с общим направлением потока. Их движение неупорядоченное, хаотичное. Эпюра скорости имеет вид усеченной параболы, (см. рис. 7.1, б). Теплоотдача при турбулентном режиме течения тепло-
119
носителя отличается несравненно большей интенсивностью, чем при ламинарном режиме
Re < 2300 |
а |
Re > 10000
б
Рис. 7.1
Как при ламинарном, так и при турбулентном режимах движения скорость теплоносителя непосредственно на стенке равна нулю, а с увели - чением расстояния по нормали от стенки она возрастает.
Слой теплоносителя около поверхности тела, где скорость изменяется
от нуля до величины, примерно равной 0,9 |
скорости невозмущенного потока, |
|
называют |
г и д р о д и н а м и ч е с к и м |
пограничным слоем и обознача- |
ют буквой |
δд , рис.7.2. |
|
C |
о g |
а
C |
оg |
ол |
б |
Рис. 7.2 |
Tm |
оT |
Tст |
в |
Кроме того, необходимо отметить, что в турбулентном пограничном слое непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или
л а м и н а р н ы м п о д с л о е м и обозначают δл (см. рис. 7.2, б).
Если температуры стенки и теплоносителя не одинаковы, то вблизи стенки образуется тепловой пограничный слой δт (см. рис.7.2, в). В нем температура изменяется от Tcm до ≈ Tm , т.е. все изменение температуры происходит в сравнительно тонком слое, непосредственно прилегающем к поверхности теплоотдачи. Значения толщин δд и δт в общем случае не равны, соотношение между ними зависит от рода жидкости. Однако изменения в δд приводят к изменениям δт. С увеличением скорости теплоносителя значения толщин δд , δт и δл уменьшаются.
120
