книги / Прикладной статистический анализ в горном деле (Многомерная математическая статистика)

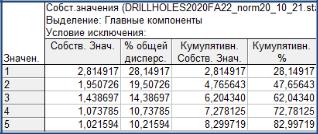
В анализе используется 10 исходных переменных, каждая нормированная переменная имеет дисперсию, равную единице. Тогда общая дисперсия данных составляет 10. Первая факторная переменная объясняет 2,81 частей от 10 единиц. Это составляет 2,81·100 / 10 = 28,1 % общей дисперсии. Вклад остальных факторных переменных можно рассчитать аналогичным образом, вычисления приведены во втором столбце таблицы. В третьем столбце приведены накопленные собственные значения, а в последнем – накопленный процент объяснения общей дисперсии, он составляет 82,997 %. Это хороший общий результат, считается, что факторный анализ должен объяснять не менее 60–70 % общей дисперсии. Детальный вклад каждой исходной переменной в результаты факторного анализа отображают факторные нагрузки и факторные веса.

Таблица 5.2 Собственные значения факторов (больше единицы)

Второй – критерий каменистой осыпи, с ним мы уже встречались в главе, посвящённой кластерному анализу. Это графический метод, предложенный Кэттелем (Cattell, 1966). На графике отображаются собственные значения, представленные в таблице ранее, в виде простого графика. Считается, если непрерывное падение собственных значений замедляется и кривая уровня остальных собственных значений становится пологой, отражая только случайный «шум» (рис. 5.6), то точка перегиба графика и является границей отбора последнего фактора.

Практика использования факторного анализа показала, что критерий Кайзера иногда завышает количество факторов, а

131

график каменистой осыпи предлагает оставить в анализе слишком мало факторов. В условиях, когда в ФА анализируем небольшое число факторов и много переменных, оба критерия работают достаточно хорошо [80].

После проведения анализа необходимо получить ответы на вопросы, как понимать и использовать полученное решение, какое оно будет иметь содержательное толкование. Для ответа на них обычно исследуется несколько вариантов решений с различным числом латентных переменных, только после этого перебора выбирается одно наиболее приемлемое. Этот вопрос далее будет рассматриваться детально.

Рис. 5.6. График каменистой осыпи

На графике каменистой осыпи видно, что пятое собственное значение больше единицы, по этому ограничению в анализе представлено всего 5 значений из 10. Но на этом графике видно, что выполаживание графика начинается после четвёртого корня. Возможно, пятый фактор будет лишним.

В закладке «Описательные» имеются возможности посмотреть коэффициенты корреляций и основные статистики, помимо этого, построить уравнение множественной регрессии

(рис. 5.7).

132

Основные результаты факторного анализа выражаются в наборах факторных нагрузок и факторных весов.

Таблица 5.3

Факторные нагрузки

В табл. 5.3 можно вычислить значения основных факторов из выражения (5.3). В выражении сi коэффициент перед исходной переменной Xi, например:

F1 = 0,530302∙GDA – 0,247271∙POWER + 0,109484∙KCL + ... .

Из этой таблицы можно получить и исходные переменные, например:

POWER = – 0,247271∙F1 + 0,248484∙F2 + ... – 0,342126∙F5.

Для вычисления собственных значений первой латентной переменной (фактора 1) достаточно возвести в квадрат факторные нагрузки, после чего сложить их по строке (табл. 5.4).

Вычисленное собственное значение латентной переменной разделим на количество исходных переменных. Частное от деления покажет, какая доля дисперсии объясняется данным фактором: 2,814 / 10 = 0,28 %. Из таблицы следует, что первая латентная переменная объясняет около 28 % информации.

134

Численные значения каждой латентной переменной (каждого фактора) именуют факторными весами для каждой исходной переменной. Та исходная переменная, у которой наибольшее значение факторного веса, обладает большей степенью влияния на фактор. Можно предположить, что она определяет свойства данного фактора. В таблице факторных весов содержится n строк, по числу исходных переменных и k столбцов по числу латентных факторов. Таким образом, данные о факторных нагрузках позволяют сформулировать выводы о наборе исходных признаков, отражающих тот или иной фактор, об относительном весе отдельной переменной в структуре каждого фактора. В свою очередь, данные о факторных весах определяют ранжирование переменных по каждому фактору. Значения факторных весов можно рассматривать как значения индекса, характеризующего уровень влияния переменных в рассматриваемом факторе.

Так, фактор 1 имеет значимую нагрузку с высотной отметкой пробы (UP_BORDER), можно сказать, что этот фактор отвечает за геопространственное положение проб по глубине залегания пласта (табл. 5.4). Немного ниже значимости нагрузка у координаты Х и химических компонентов. У второго фактора значимые нагрузки имеют HO и вероятность проявления ГДЯ. Следующие два фактора не имеют значимых нагрузок, но пятый фактор связан с координатой Y.

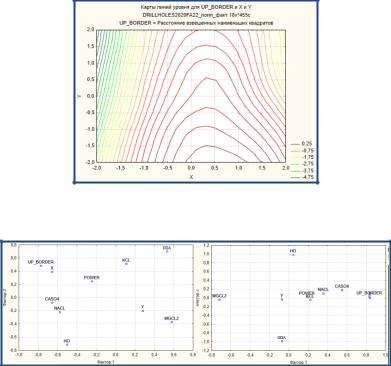
Интерпретировать их назначение пока трудно. Возможно, потребуется дальнейшее улучшение факторных нагрузок путём вращения факторов, уменьшения количества исходных переменных, которые не дают ощутимого уменьшения дисперсии или уменьшения количества факторов. Для интерпретации факторов необходимы детальные знания об изучаемом процессе. Любая дополнительная информация может помочь трактовать назначение факторов. Например, изолинии распространения высотной отметки кровли пласта, представленные на рис. 5.9, объясняют её зависимость от координат.

Уменьшение количества факторов, возможно, будет являться стимулом к концентрации исходных факторов. Значи-

136

мость установлена на уровне 0,7. В нагрузках имеются близкие к этому уровню значения.

Рис. 5.9. Изолинии высотных отметок в системе координат (данные нормированы)

Рис. 5.10. Графики факторных нагрузок в осях первых двух факторов: а – до вращения, б – после вращения факторов

Можно вывести и трёхмерное изображение (рис. 5.11). На первом этапе попробуем вращение факторов, метод выберем биквартимакс нормализованный. При вращении изменяется плоскость проекции факторов, в результате чего факторы становятся ближе друг к другу. На рис. 5.10 заметно изменение в положении факторов. Такое вращение не изменит вычисленные собственные значения, но повлияет на величины факторных нагрузок.

137

ные (координата Х; высотная отметка пласта UP_BORDER). Второй фактор включает значимые переменные, связанные с газодинамическими явлениями – нерастворимый остаток НО и вероятность проявления ГДЯ. Третий фактор содержит переменные по химическому составу сильвинитового пласта. Четвёртый и пятый факторы имеют всего по одной значимой переменной, каждая из них отвечает за положение пробы в пространстве, в ходе дальнейшего анализа, возможно, их понадобиться объединить, уменьшая количество факторов.

В факторном анализе тесная связь исходной переменной с рассматриваемым латентным фактором предполагает и большое значение факторной нагрузки. Положительный знак у факторной нагрузки указывает на прямую зависимость исходной переменной с латентной, а отрицательный знак – на обратную связь той же переменной с фактором.

С учётом этих замечаний настораживает отсутствие нагрузки по исходной переменной CaSO4. Если она не имеет значимых нагрузок на факторы, следовательно, она является лишней в списке исходных данных и её можно удалить из анализа.

При рассмотрении редуцированной матрицы в п. 5.1 обращалось внимание, что на её главной диагонали стоят не единицы, поясняющие всю дисперсию переменной, а величина объясняемой части дисперсии, именуемая общностью. Эта статистика определяет вклад переменной в пояснение дисперсии, её полезность. Поэтому, прежде чем принимать решение об удалении каких-либо переменных, необходимо выполнить анализ их влияния на факторы.

Вращение факторов. После выполнения первых расчётов ориентация факторных осей произвольна, что хорошо заметно на графиках (см. рис. 5.10). И в ряде случаев интерпретация результатов факторного анализа становится неоднозначной. Для решения вопроса о распределении переменных по факторам используется приём вращения факторов относительно переменных таким образом, чтобы получить наиболее компактное расположение переменных в пространстве факторов. Соотношение признаков в осях факторов при этом никак не изменится. Ранее от-

139

мечалось, что связь между переменной и фактором отражает факторная нагрузка, она, являясь подобием коэффициента корреляции, может принимать значения от – 1 до + 1. В ходе изыскания простой структуры целесообразно стараться получить на каждую переменную максимальное число высоких факторных нагрузок по одним факторам. По другим факторам нагрузки должны быть минимальными. Используя этот подход, ФА стремится сделать так, чтобы одну группу переменных можно было с большой вероятностью объяснить влиянием одних факторов, а другую – других. В этом случае каждая переменная имеет наиболее простое факторное объяснение, т.е. характеризуется преобладающим влиянием некоторого одного фактора и в меньшей степени связана с другими факторами. И наоборот: один фактор должен быть специфическим образом связан с одной группой переменных и не связан с другими переменными. В идеальном варианте хорошая структура получается тогда, когда все переменные располагаются на соответствующих факторных осях, т.е. имеют высокие факторные нагрузки только по одному фактору, а по остальным – нулевые.

В процессе вращения факторов происходит перераспределение дисперсии по заданному методу. Вращение применяется после выделения факторов для увеличения высоких корреляций и для уменьшения малых. В программе Statistica используется несколько методов вращения, один из наиболее популярных – метод «варимакс», который представляет собой процедуру максимизации дисперсий. Вращение может быть ортогональным и косоугольным. Цель ортогональных вращений – определение простой структуры факторных нагрузок, целью большинства косоугольных вращений является определение простой структуры вторичных факторов, т.е. косоугольное вращение следует использовать в частных случаях. Чаще других используются ортогональные методы вращения:

• варимакс критерий – индекс сложности каждого фактора, который пропорционален числу переменных, связанных с этим фактором. Метод «варимакс» максимизирует разброс квадратов нагрузок для каждого фактора, что приводит к увеличению боль-

140