Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Теория функций комплексного переменного

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Функция	w =	1 .	Преобразование	w =	1	является кон-
		z			z

формным во всей расширенной комплексной плоскости.

Преобразование w = 1z состоит из двух симметричных от-

ражений: относительно единичной окружности и относительно действительной оси.

Точки M и M1 называются симметричными относительно единичной окружности, если

1)они находятся на одном луче, выходящем из центра окружности, из начала координат;

2)произведение их расстояний от центра окружности рав-

но квадрату радиуса окружности OM OM1 =1.

Если центр окружности находится в начале координат и точка M изображает комплексное число z, то точка M1 со-

ответствует		комплексному числу			R	.	Окружности		(прямые)
ответствует		комплексному числу				.	Окружности		(прямые)
					z
при отображении w = 1			переходят в				окружности		(прямые).
		z
Точке	z = 0	соответствует точка		w = ∞ , точке				z = ∞ – точка
w = 0.	Неподвижные точки отображения w = 1							– точки z =1
							z		1
							z

и z2 = −1.

Для того чтобы найти образ области G при конформном отображении, используют принцип соответствия границ, со-

гласно которому конформное отображение одной области на другую определяется взаимно однозначным соответствием между их границами.

Пусть в плоскости z граница L области G задана уравнением F(x; y) = 0. Найдем уравнение Φ(u;v) = 0 образа границы L в плоскости w при конформном отображении с по-

мощью функции w = f (z). Для этого выделим действительную

и мнимую часть функции	w = f (z).	Так как w =u +iv,
z = x +iy, то задание функции	z = f (z)	равносильно заданию
двух функций u =u(x; y) , v = v(x; y). Далее, из системы урав-
нений
u =u(x, y),
v = v(x, y),		(4.30)
F(x, y) = 0

исключим переменные x и y.

В результате получим искомое

уравнение Φ(u;v) = 0.

Линия Φ(u;v) = 0

разбивает

плоскость

w на непересе-

кающиеся области Γ1 и Γ2.

Для того чтобы найти образ области G,

нужно взять про-

извольную пробную точку z0

из области

G и найти ее об-

раз w0 .

Если w0 Γ1,

то образом области

G будет являться

область Γ1. В противном случае – область Γ2.

Пример 4.10. Найти образ окружности

=3 при отобра-

жении w = 4 .

Пусть z = x +iy,

w =u +iv. Тогда соотношение w =

4 при-

мет вид u +iv =

−i

4 y

, откуда u =

x +iy

x2 + y2

v = −

4 y

x2 + y2

Система уравнений для определения образа окружности z =3 имеет вид

u =

(1)

+ y

(2)

+ y

x2 + y2 =9.

(3)

Исключим из этой системы x и y. Так как x2 + y2 =9, то

из формул (1) и (2) следует:

x = 9 u, y = −9 v.

Значит в силу

−

=9,

т.е. u

Таким

формулы (3),

образом, окружность

при отображении w =

переходит

в окружность с центром в начале координат, радиуса R = 43 .

Пример 4.11. Найти образ области z ≤3 при отображе-

нии w = 4z .

Образом границы рассматриваемой области в силу примера 4.10 является окружность с центром в начале координат, ра-

диусом R = 43 . Рассмотрим пробную точку z =1. Ее образом является точка w = 4, лежащая вне полученной окружности.

Следовательно, образом круга z ≤3 является область w ≥ 43 (рис. 11).

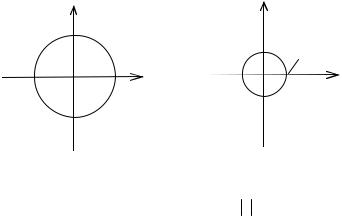
y	z	v	w
	3		4 3
0	x	0	u
0	x	0	u

Рис. 11

Пример 4.12. Найти образ области z ≥3 при отображении w = z − 4z .

Найдем образ границы рассматриваемой области.

Пусть z = x +iy,

w =u +iv. Тогда соотношение

w = z −

4 y

примет вид

u +iv = x +iy −

= x +

+i y −

+iy

+ y

откуда u = x 1+

, v

= y 1

−

+ y

Из системы уравнений

u = x

+ y

v = y

−

+ y

x2 + y2

находим уравнение для образа границы рассматриваемой об-

	9		2	9		2		u2				v2
ласти:			u	+		v	=9 или				+				=1 . Таким обра-
		13			5			(13	9 )	2		(5	9 )	2

зом, образом окружности	z	=3 при преобразовании w = z −	4
зом, образом окружности	z	=3 при преобразовании w = z −	4
			z
			z

является эллипс с центром в начале координат и полуосями, равными 139 и 59 .

В качестве контрольной точки возьмем точку z = 4. Ее образом является точка w =3, лежащая внутри эллипса. Следовательно, образом искомой области является множест-

во точек				плоскости			W ,	определяемое			неравенством
	u2			v2
		+			≤1	и	представляющее			собой	внутренность
	(139 )2		(59 )2
эллипса.
					Интегрирование функции
					комплексного переменного
	Пусть однозначная функция								f (z)	определена и непре-
рывна в области G, а							L – кусочно-гладкая незамкнутая кри-
вая, лежащая в области G.
	Пусть			z = x +iy, f (z) =u +iv,					где u =u(x; y), v = v(x; y) –
действительные функции переменных x и y.
	Вычисление					интеграла от		функции		f (z)	комплексного

переменного z сводится к вычислению двух криволинейных интегралов по координатам функции действительных переменных x и y по формуле

∫ f (z)dz = ∫ udx −vdy +i∫ vdx +udy.			(4.31)
L	L	L
			45

Интеграл ∫ f (z)dz, вообще говоря, зависит от пути интег-

рирования L.

Если кривая L определяется уравнением y = y(x), a ≤ x ≤b, то равенство (4.31) примет вид

∫ f (z)dz = ∫b (u(x; y(x) −v(x; y(x) y′(x))dx +

+ib∫(v(x; y(x) +u(x; y(x) y′(x))dx.

Пример 4.13. Вычислить интеграл ∫ z2dz по дуге кубиче-

ской параболы y = x3 , соединяющей точки z1 = 0 и z2 =1+i. Функция f (z) = z2 может быть задана следующим обра-

зом: z2 =( x +iy)2 =(x2 − y2 )+i2xy. Следовательно,

∫ z2dz = ∫ ((x2 − y2 )+i2xy)(dx +idy) =

=∫ (x2 − y2 )dx −2xydy +i∫ 2xydx +(x2 − y2 )dy.

	L		L
	Уравнение линии L запишем в виде z = x +iy.						На дуге L
справедливо равенство y = x3 ,			0 ≤ х ≤1.
	Поэтому
	1		1
∫ z2dz = ∫(x2 − x6 )dx −2xx3 3x2dx +i∫ 2xx3dx +(x2 − x6 )3x2dx =
L	0		0
1	1		x3		1			x9	1
1	1		x3		1			x9	1
= ∫	(x2 −7x6 )dx +i∫	(5x4 −3x8 )dx =		− x7		+ i x5 −			=
= ∫	(x2 −7x6 )dx +i∫	(5x4 −3x8 )dx =		− x7		+ i x5 −			=
0	0		3		0			3	0
46			3		0				0
46

= −23 + 23 i.

Если

кривая L

задана параметрическими

уравнениями

x = x(t),

y = y(t),

t1 ≤t ≤t2 ,

то равенство (4.31) примет вид

∫

(

)

−

(

)

f (z)dz

= ∫ (

x(t); y(t)

x′(t)

x(t); y(t)

y′(t) dt

Lt1

+it∫2 (v( x(t); y(t)) x′(t) +u ( x(t); y(t)) y′(t))dt.

∫ (z2 + zz )dz, где L –

Пример 4.14. Вычислить интеграл

дуга окружности

=1,

0 ≤ arg z ≤ π.

Положим z = eit , тогда dz =ieit dt,

0 ≤t ≤ π. Поэтому

∫ (z2 + zz )dz =

(ei3t +eit )dt =

∫

(ei2t +1)ieit dt = i∫

i3t

−

Если f (z) – аналитическая функция в односвязной облас-

ти G, то интеграл ∫ f (z)dz

не зависит от пути интегрирования,

а зависит только от координат начальной и конечной точек z1 и z2. В этом случае справедливо равенство

			z2
		∫ f (z)dz = ∫ f (z)dz.		(4.32)
		L	z1
Если	кривая	L задана	параметрическими	уравнениями
x = x(t),	y = y(t) ,	t1 ≤t ≤t2 , то равенство (4.32) примет вид
			t2
		∫ f (z)dz = ∫ f ( z(t)) z′(t)dt.
		L	t1
				47

Пример 4.15. Вычислить интеграл ∫ ez dz , где L – отрезок

прямой y = −x , соединяющий точки z1 = 0

и z2 = π−iπ.

Запишем

параметрические

уравнения

линии

L : x =t ,

y = −t , или в комплексной форме z =t −it ,

где параметр t из-

меняется от 0 до π. Тогда

dz =

t+it

(1+i)t

1−i

(1+i)t

∫ e

(1−i)dt = (1−i)∫ e

1+i

(

)

(

)

(

)

= −i

e(1+i)π

−1

= −i

eiπeπ −1

= i

eπ +1 .

Если функция f (z)

аналитична в односвязной областиG ,

содержащей точки z1

и z2 , то имеет место формула Ньютона–

Лейбница

∫ f (z)dz = Φ(z2 ) −Φ(z1 ),

(4.33)

где Φ(z) – некоторая первообразная для функции

f (z) .

Пример 4.16. Вычислить интеграл

∫ (

)

3z2 +2z dz , где L –

дуга параболы y = x2

между точками z

=1−i и z

= 2 +i .

Так как функция

f (z) =3z2 +2z

аналитична на всей ком-

плексной плоскости, то рассматриваемый интеграл не зависит от пути интегрирования и может быть вычислен с помощью формулы Ньютона–Лейбница

∫	(			)		(		) 1−i
		3z2	+	2z dz	=		z3 + z2		2+i = (2	+i)3 +(2 +i)2 −(1−i)3 −(1−i)2 =
L		=8 +12i −6 −i +4 +4i −1−1+3i +3 −i −1+ 2i +1 = 7 +19i.
		=8 +12i −6 −i +4 +4i −1−1+3i +3 −i −1+ 2i +1 = 7 +19i.

Замена переменных в интегралах от функции комплексного переменного производится аналогично случаю функции действительного переменного. Пусть аналитическая функция

z = ϕ(w) отображает взаимно		однозначно контур L z-плос-
кости на контур L1 w-плоскости. Тогда
∫ f (z)dz = ∫ f (ϕ(w))ϕ′(w)dw.			(4.34)
L	L1
Пример 4.17. Вычислить интеграл ∫ z sin z2dz , где L – от-
		L
резок AB прямой, zA = 0,	zB =1+i.
Функция z = w2 аналитична всюду. Тогда
∫ z sin z2dz	1+i	1 sin z2 (z2 )′dz =
	= ∫
L	0	2

= −12 cos z2 10+i = 12 (1−cos 2i) = 12 (1−ch 2) .

Формула интегрирования по частям в интегралах от функции комплексного переменного также аналогична случаю функции действительного переменного. Если функции f (z)

и ϕ(z) аналитичны в односвязной области G , точки z1 и z2 принадлежат области G , то

z					z
z					z
∫2 f (z)ϕ′(z)dz =[ f (z)ϕ(z)]				z2 − ∫2 ϕ(z) f ′(z)dz.
z				z1	z
1					1
					i
Пример 4.18. Вычислить интеграл ∫ z cos zdz .
					0
Функции f (z) = z			и ϕ(z) = cos z аналитичны всюду.
Применяя формулу интегрирования по частям, получим
i		i				i
∫ z cos zdz		= ∫ z(sin z)′dz = ( z sin z)				i0 −∫sin zdz	=
∫ z cos zdz		= ∫ z(sin z)′dz = ( z sin z)				i0 −∫sin zdz	=
0		0			0

= (isin z +cos z)	i	=i sin i −sin 0 +cosi −cos 0 =i ish1+cos1−1 =
	0
							49

= −sh1+ch1−1 = −e1 −2e−1 + e1 +2e−1 −1 =

= −e +e−1 +e +e−1 −2 = e−1 −1. 2

Пример 4.19. Вычислить интеграл от функции комплекс-

ного переменного

∫

z3dz ,

где

AB – отрезок прямой, zA = 0 ,

zB =i .

Так как подынтегральная функция

f (z) = z3

аналитична

всюду, то

можно

воспользоваться

формулой

Ньютона–

Лейбница ∫

z3dz = ∫ z3dz =

−0 =

Пример 4.20. Вычислить интеграл от функции комплекс-

ного переменного

∫

z dz,

где

ABC – ломаная, zA = 0, zB =i ,

ABC

zc =1+i .

Подынтегральная функция f (z) = z определена и непрерывна всюду, ломаная ABC представляет собой кусочногладкую кривую, поэтому искомый интеграл сводится к вычислению двух криволинейных интегралов по координатам по формуле

∫ f (z)dz =∫udx −vdy +i∫ vdx +udy.

ГГ Г

Следовательно,

∫ z dz =	∫ (x −iy)(dx +idy) =	∫	xdx + ydy +i ∫ −ydx + xdy.
ABC	ABC	ABC	ABC

Воспользуемся свойством аддитивности криволинейного интеграла:

∫ f (z)dz = ∫ f (z)dz + ∫ f (z)dz.

ABC AB BC

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в папке книги

#
19.11.202327.99 Mб1Теория упругости микронеоднородных сред..pdf
#
12.11.202311.07 Mб1Теория упругости неоднородных тел..pdf
#
12.11.20238.54 Mб6Теория упругости. Задача Сен-Венана. Плоская задача теории упругости.pdf
#
12.11.20235.05 Mб2Теория упругости. Ч. 1 Основные уравнения механики сплошных сред. Вариационные методы.pdf
#
12.11.202321.88 Mб2Теория упругости..pdf
#
12.11.20231.22 Mб5Теория функций комплексного переменного..pdf
#
19.11.202328.91 Mб2Теория функций комплексной переменной..pdf
#
12.11.20235.34 Mб3Теория химических реакторов введение в основной курс..pdf
#
12.11.20236.48 Mб1Теория химических реакторов. Введение в основные разделы курса.pdf
#
12.11.20232.15 Mб15Теория электрической связи. Основные понятия.pdf
#
13.11.202324.95 Mб10Теория электрической связи. Помехоустойчивая передача данных в информационно-управляющих и телекоммуникационных системах модели, алгоритмы, структуры.pdf