книги / Теория функций комплексного переменного

ции f (z) , если да – восстановить ее при условии f (0) =1 .

Решение

Найдем частные производные:

∂u

= 2e2x cos 2 y,

∂u

= −2e2 х sin 2 y,

∂x

∂y

∂2u

= 4e2 x cos 2 y,

∂2u

= −4e2 х cos 2 y.

∂x2

∂y2

Проверим формулу

∂2ϕ

+

∂2ϕ

= 0.

∂x2

∂y2

∂2u

+

∂2u = 4e2 x cos 2 y −4e2 х cos 2 y = 0 , (x, y) R2 .

∂x2

∂y2

Видим, что функция

u(x, y) гармоническая в

плоско-

сти

и,

следовательно, существует такая аналитическая на

множестве

комплексных чисел

функция f (z) , что

f (z) =

∂v

=

∂u = 2e2 x cos 2 y,

(1)

∂y

∂x

∂v

= −∂u

= 2e2 х sin 2 y.

(2)

∂x

∂y

v = e2 x sin 2 y +C(x) .

(3)

∂v = 2e2 х sin 2 y +

С′(х).

∂x

Сопоставляя результат с полученным в формуле (2), име-

ем С′(х) = 0 , откуда С(х) = А.

Таким образом,

v = e2 x sin 2 y + А

и

f (z) =u +iv = e2 x cos 2 y +ie2 x sin 2 y +iA =

= e2 x (cos 2 y +i sin 2y) +iA = e2 xe2iy +iA =

= e2( x+iy) +iA = e2 z +iA.

Учитывая условие f (0) =1 , получаем A = 0 .

Итак, f (z) = e2 z .

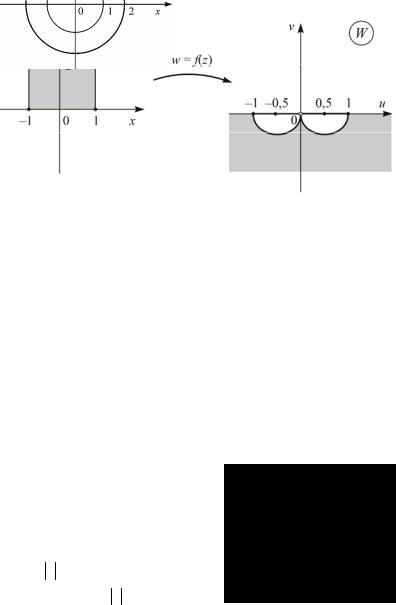
Задание 7. Найти область плоскости W , в которую ото-

1

Re z

≤1,

бражается с помощью функции w =

область D:

z

Im z ≥ 0

плоскости Z.

в плоскости W

при отображении с помощью функции

w = f (z) =u +iv,

нужно исключить x и у из уравнений

u =u(x, y),

(1)

v = v(x, y),

F(x, y) = 0.

Если кривая задана параметрическими уравнениями

x = x(t),

или

z = z(t) = x(t) +iy(t) ,

y = y(t)

то параметрические уравнения её образа

при отображении

w = f (z) =u +iv будут выглядеть следующим образом:

u =u(x(t), y(t)) =U (t),

= v(x(t), y(t)) =V (t).

v

В данном примере граница области

D состоит из трех

частей: L1 : x = −1,

y ≥ 0,

L2 : x =1, y ≥ 0,

L3 : y = 0,−1 ≤ x ≤1 .

w =

1

=

1

=

x −iy

=

x

+i

−y

;

z

x +iy

x2 + y2

x2 + y2

x2 + y2

u =

x

,

v = −

y

.

x

2 + y2

x2 + y2

u =

x

,

x

2

+ y

2

u = −

1

,

y

1+ y

2

v = −

,

x

2

+ y

2

y

v = −

.

1+ y

2

x = −1,

y ≥ 0

u = −

1

≤ 0.

1+ y2

Окончательное

уравнение

границы

L1:

u

+ 1

2 +v2

= 1

2

4

при u ≤ 0, v ≤ 0 .

Аналогично находим

образ

L2 :

u

−

1

2

+v2 = 1

при

2

4

u ≥ 0, v ≤ 0.

Образ L3 находим из системы

u =

x

,

x

2

+ y

2

y

u =

1

,

v = −

,

x

x

2

+ y

2

v

= 0.

= 0,

−1 ≤ x ≤1

y

Следовательно,

образ

границы

L3:

v = 0,

u ≥1

при

Для изображения образа

области D на плоскости W

возьмем контрольную точку.

Точка z =i обратится в точку

w = −i.

94

функции f (z)

по степеням z − z0 . Указать главную и правиль-

ную части ряда.

а) f (z) =

2z +1

, z

= 0 ;

z2 + z −2

0

б) f (z) =

2z +1

,

z0 =1 .

(z −1)(z +

2)

Решение

а) Функция f (z) =

2z +1

имеет две конечные особые

z2 + z −

2

точки z1 =1 и

z2 = −2 . Отметим их на плоскости Z, проведем

ветственно

через точки

z1 =1

и z2 = −2.

Следовательно,

име-

3) в окрестности бесконечно удаленной точки

z

> 2 .

Найдем ряды Лорана для функции

f (z)

в каждой из этих

областей.

Представим функцию

f (z)

в виде суммы элементарных

дробей:

2z +1

=

1

+

1

.

z2 + z −

2

z

−1

z +2

1) В круге

z

<1 функция расладывается в ряд Тейлора по

формуле (5.9).

Приведем элементарные дроби

1

и

1

к виду

1

,

z −1

z +2

1

−t

где

t

<1 при

z

<1:

f (z) = −

1

+

1 1

.

1

− z

2 1+

z

2

Так как в рассматриваемой области

z

<1, то в силу фор-

мулы (5.15)

=1+ z + z2 + z3 +... + zn +... = ∑ zn .

1

∞

1− z

n=0

Так как

z

<1, то тем более

z

<1 (если

z

<1, то тем бо-

2

< 2),

лее

z

следовательно, в силу формулы (5.15)

1

z

z

2

z

3

z

n

∞

z

n

=1−

+

−

+... +(−1)n

+... =

∑ (

−1)n

.

z

2n

2n

1+

2 4

8

n=0

2

1

1

1

∞

1

∞

zn

−

+

= −∑ zn +

∑ (−1)n

=

− z

z

2n

1

2

1+

n=0

2 n=0

2

∞

n

∞

n zn

∞

(−1)n

n

= −∑ z

+ ∑ (−1)

= ∑

−1 z

.

2n+1

2n+1

n=0

n=0

n=0

рассматриваемую функцию в виде

f (z)

= 1

1

+

1 1

.

z 1− 1

2 1+

z

z

2

Первое слагаемое раскладываем в области

z

>1 ,

т.е. за-

писываем главную часть ряда Лорана, второе – в круге

z

< 2 –

правильная часть.

Применяя формулы (5.16) и (5.15), получим

1

1

1

1

1

∞

1

=1

+

+

+

+...

+

+... =

∑

,

1

z

z2

z3

zn

zn

n=0

1− z

1

z

z

2

z

3

z

n

∞

(

−1)n

z

n

=1

−

+

−

+... +(−1)n

+... =

∑

.

z

2n

2n

1+

2 4

8

n=0

2

Записываем окончательный результат:

1

1

1

1

∞ 1

∞

zn

+

=

∑

+ ∑ (−1)n

.

z

1

2

z

2n+1

n=1 zn

n=0

1− z

1

+

2