
1465
.pdfВзяв интеграл от этого многочлена при р = 1, 2, 3, 4, получим следующие базисные функции:
φ2 |
= ξ2 −1, |
φ3 |
= 2(ξ3 − ξ), |
|
(4.9) |
φ4 |
= 0,25(15ξ4 −18ξ2 + 3), |
φ5 = 7 ξ5 −10ξ3 + 3ξ.
Функции ϕ 0 и ϕ 1 имеют вид (4.4). Производные этих функций ортогональны, что приводит к матрице разрешающих соотношений диагональной формы.
Еще один вид элементов – эрмитовы элементы. Базисные функции для них могут быть получены аналогичным образом как для лагранжевых элементов, но с использованием полиномов Эрмита вместо полиномов Лагранжа. При этом в каждом узле элемента будут определяться не только значения искомой функции, но и ее производные [5].
Рассмотрим одномерный элемент с s узлами, причем узлы не обязательно расположены равномерно. Пусть у каждого узла две степени сво-
боды – функция θ и ее производная ∂θ |
s/∂ x. Аппроксимация искомой |
||
функции на элементе имеет вид |
|
|
|
θ = ∑ φ0i (x)θi + φ1i (x) ∂ θi . |
|||
s |
|
|
|
i=1 |
|
∂ x |
|
Первый индекс у базисной функции ϕ ji обозначает порядок дифференцирования соответствующей узловой переменной, а второй – номер узла. Для того чтобы выполнялись условия
θ(xk ) = θk , |
∂ θ(xk ) |
=∂ |
θk |
, |
∂ x |
|
|||
|
∂ x |
|||
базисные функции должны удовлетворять соотношениям
φ0i (xi ) =1, φ′0i (xi ) = 0, φ0i (xi ) = 0, φ′0i (xi ) = 0,
φ1i (xi ) = 0,
φ′ (x ) =1,
1i i
φ1i (xi ) = 0, φ1′i (xi ) = 0.
211
Этим условиям удовлетворяют полиномы Эрмита [7]
s |
|
2 |
|
s |
|
− x |
||
(x |
− x j ) |
|
x |
|||||
φ0i (x) = ∏ |
|
∑ |
||||||
|
|
|
1 + 2 |
i |
|
, |
||
|
− x j ) |
2 |
|
|
||||
j=1, j≠ i (xi |
|
|
j=1, j≠ i xi |
− x j |
||||
|
|
|
|
|
|
|
|
|
s |
(x |
− x j ) |
2 |
|
||
φ1i (x) = ∏ |
|
|
(x − xi ) . |
|||
(x |
− x |
) |
2 |
|||
j=1, j≠ i |
|
|
||||
i |
j |
|
|
|
|
|
В качестве конкретного примера рассмотрим случай s = 2. Тогда
|
∂ θ1 |
∂ θ2 |
|
|
θ = φ01 (x)θ1 + φ11 (x) |
|
+ φ02 (x)θ2 + φ12 (x) |
|
, |
∂ x |
∂ x |
|||
где базисные функции
|
|
|
(x |
− x)2 |
|
|
|
x |
− x |
|
|
|||||
φ01 (x) = |
|
|
2 |
|
|
|
|
|
1 |
+ 2 |
|
|
|
1 |
|
, |
|
|
(x2 − x1 ) |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x2 |
− x1 |
|||||||
φ02 (x) = |
|
|
(x |
− x )2 |
|
x |
− x |
|
|
|||||||
|
|
|
1 |
2 1 |
+ 2 |
2 |
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(x2 − x1 ) |
|
|
x2 − x1 |
|
|||||||||
φ11 (x) = |
|
|
(x |
− x)2 |
|
|
− x1 ), |
|
|
|
|
|||||
2 |
|
|
|
(x |
|
|
|
|
||||||||
(x |
− x )2 |
|
|
|
|
|
||||||||||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
φ12 (x) = |
|
(x − x )2 |
|
(x |
− x2 ). |
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|||||||
(x |
− x )2 |
|
|
|
|
|
||||||||||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
В локальных нормированных координатах аппроксимация и базисные функции принимают вид
|
∂ θ1 |
∂ θ2 |
|
|
θ = φ01 (ξ)θ1 + φ11(ξ) |
|
+ φ02 (ξ)θ2 + φ12 (ξ) |
|
, |
∂ x |
∂ x |
|||
φ01 (ξ) =1 − 3ξ2 + 2ξ3 , |
φ02 (ξ) = 3ξ2 − 2ξ3 , |
|
||
φ11 (ξ) = hξ(1 − ξ)2 , |
|
φ12 (ξ) = h(ξ3 − ξ2 ). |
|
|
Узловые производные по координате x заменяются на производные по ξ : ∂ θ /∂ x= h−∂1 θ∂/ ξ, при этом величина h = x2 – x1 в последних соотношениях сокращается.
212
Описанная процедура может быть обобщена включением дополнительно к функции и ее первым производным также производных более высокого порядка. Для двумерных элементов базисные функции получаются в виде произведения одномерных базисных функций.
4.2.2. Двумерные базисные функции высших степеней
Двумерные базисные функции для прямоугольников. Простой пря-
моугольный элемент может быть получен следующим образом. Вводится локальная нормированная система координат ( −1 ≤ξ, η ≤1) (рис. 4.2, а)
ξ = 2(x − xce ) / hxe , dξ = 2dx / hxe ,
(4.10)
η= 2( y − yce ) / hye , dη= 2dy / hye ,
где (xce , yce ) – координаты центра элемента в системе xOy.
С каждым элементом ассоциируются четыре узла (ξ l,η l), l = 0, 1, 2, 3. Пусть
ξl = ξξl e , ηl = ηηl e .
Тогда билинейные базисные функции имеют вид
φl = (1 / 4)(1 + ξl )(1 + ηl ), l = 0, 1, 2, 3 , |
(4.11) |
что получено простым перемножением одномерных базисных функций. Такой элемент называется лагранжевым элементом первой степени.
Базисные функции лагранжева элемента вычисляются перемножением отвечающих этому узлу стандартных одномерных функций от х и у. Действительно, если узлы элемента находятся в вершинах прямоугольной сетки, то, сопоставляя каждому узлу двойной индекс (r, s), соответствующую узлу (r, s) базисную функцию можно записать как
φers (ξ, η) = Λ rp (ξ)Λ sp (η) , |
(4.12) |
где Λ rp – многочлен Лагранжа степени p, определенный соотношениями (4.4)–(4.6). На рис. 4.2 приведен вид некоторых лагранжевых базисных функций на прямоугольном элементе. Отметим, что φers будет равно единице только в узле (r, s) и тождественно равно нулю во всех других узлах.
213
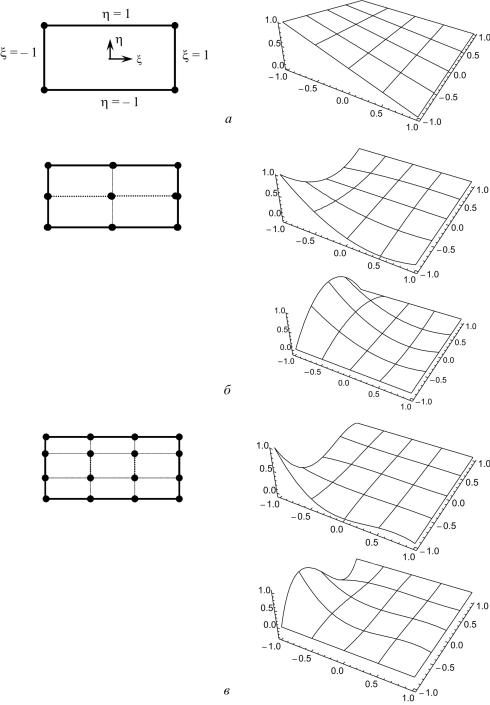
Рис. 4.2. Три элемента лагранжева семейства и некоторые соответствующие базисные функции: а – элемент первого порядка; б – элемент второго порядка; в – элемент третьего порядка
214
Отметим, что поскольку базисные функции (4.12) определены произведением многочленов степени р отдельно от х и у, то число членов
вэтом произведении превышает число членов, необходимое для воспроизведения многочлена степени р от х и у.
На рис. 4.3, а построен треугольник Паскаля, по которому можно определить число членов в многочлене произвольной степени (например
вкубическом многочлене – 10 членов). На рис. 4.3, б дополнительно выделены шесть членов, появляющихся в кубической лагранжевой базисной функции, определенной соотношением (4.12). Можно уменьшить число узлов, ассоциированных с элементами высокого порядка, обеспечив, чтобы базисные функции элемента содержали бы только члены, входящие
вмногочлен соответствующей степени. Это семейство так называемых серендиповых элементов (рис. 4.3, в). Здесь узлы располагаются (по возможности) на границах элементов, а базисные функции (для узлов, расположенных не в вершинах элемента) получаются умножением членов степени р по одной переменной на линейные члены по второй перемен-
ной (рис. 4.4, а, б).
Функции формы для четырехугольных серендиповых элементов 2-го и 3-го порядка, содержащие 8 и 12 узлов (см. рис. 4.4) соответственно, представляют собой полиномы
ϕ |
= α |
1 + α |
2 ξ |
+ α |
3η |
+ α 4 ξη + α |
5 ξ 2 |
+ α |
6 η |
2 |
+ α |
7 ξ 2 η |
+ α |
8 ξη |
2 , |
|
ϕ |
= α |
1 + α |
2 ξ |
+ α |
3η |
+ α 4 ξη |
+ α |
5 ξ 2 |
+ α |
6 η |
2 |
+ α |
7 ξ 2 η |
+ α |
8 ξη |
2 + |
|
|
+ α 9 ξ 3 + α 10 η 3 + α |
11ξ 3η + α 12 ξη 3 . |
|
|
|
|
|
||||||||
Функции формы равны нулю во всех узлах, кроме узла, номер которого совпадает с номером соответствующей функции формы; кроме того, они принимают нулевые значения вдоль всех границ элемента, которые не содержат указанного узла. Функции формы могут быть получены либо путем решения СЛАУ (аналогично тому, как это делалось для одномерной функций и для линейных функций формы на треугольнике), либо комбинированием функций, которые обращаются в нуль на границах элемента. Множество функций, равных нулю вдоль одной из сторон элемента, можно получить из функций формы для билинейного четырехугольного элемента (4.11).
215

Рис. 4.3. Треугольник Паскаля: а – заштрихованы элементы, образующие полный кубический полином; б – заштрихованы элементы, образующие кубический лагранжев полином; в – заштрихованы элементы, образующие кубический серендипов полином [3]
216

Рис. 4.4. Элементы серендипова семейства и некоторые соответствующие базисные функции: а – элемент второго порядка; б – элемент третьего порядка [8]
Итак, общая формула для четырехугольных серендиповых элементов 2-го и 3-го порядка имеет вид [9]
φβ |
= ∏4 |
Fj (α1 + α2ξ + α3η+ α4ξ2 + α5η2 ) , |
|
j=1 |
|
217
f , если узел β не принадлежит стороне j, j = 1, 2, 3, 4, где Fj = j
1, если узел β принадлежит стороне j. Здесь функции
f1 = (1 + η), f2 = (1− ξ), f3 = (1 − η), f4 = (1+ ξ).
Каждая из них обращается в нуль на одной из границ элемента. Степень многочлена в круглых скобках определяется числом имеющихся узловых условий. Его коэффициенты определяются приравниванием ϕ β к единице в узле β и нулю во всех других узловых точках, которые не
4
входят в произведение ∏ Fj . Коэффициенты α 4 и α 5 всегда равны нулю
j=1
вслучае квадратичного элемента.
Пример. Построить функцию формы для квадратичного четырехугольного элемента для 0-го узла (см. рис. 4.4, а).
Начнем с определения произведения:
∏4 |
Fj = f1 f2 f3 f4 =1 f2 f3 1 = (1 − ξ)(1− η) . |
j=1 |
|
Общее выражение для ϕ 0 имеет вид
φ0 = (1− ξ)(1− η)(α1 + α2ξ+ α3η).
Произведение (1 – ξ ) (1 – η ) тождественно обращается в нуль в узлах 3, 4, 5, 6, 7. Константы α 1, α 2 и α 3 должны быть выбраны так, чтобы ϕ 0 была равна единице в нулевом узле и нулю в узлах 1 и 7, то есть
0 : φ0 (−1; −1) = 2(α1 − α2 − α3 ) = 1, 1: φ0 (0; −1) = 2(α1 − α3 ) = 0, 7 : φ0 (−1; 0) = 2(α1 − α2 ) = 0.
Таким образом, α1 = α2 = α3 = −1 / 4.
218
Окончательно функция формы для 0-го узла имеет вид
φ0 = −1 / 4(1− ξ)(1− η)(1+ ξ+ η).
Построим функцию формы для квадратичного четырехугольного элемента для 1-го узла (см. рис. 4.4, а), который располагается в середине стороны элемента.
Определяем произведение (так как узел принадлежит только одной – первой стороне):
∏4 Fj = f1 f2 f3 f4 =1 f2 f3 f4 = (1 − ξ)(1− η)(1+ ξ) .
j=1
Общее выражение для ϕ 1 имеет вид
φ1 = (1− ξ)(1− η)(1+ ξ)(α1 + α2ξ+ α3η) .
Поскольку произведение (1 – ξ ) (1 – η ) (1 + ξ ) тождественно обращается в нуль на трех сторонах элемента, тогда остается удовлетворить только одному узловому значению ϕ 1 = 1 при ξ = 0 и η = –1, а значит, следует определить только одну константу α 1:
1: φ1(0; −1) = 2α1 =1.
Таким образом, α1 =1 / 2 .
Окончательно функция формы для 1-го узла имеет вид
φ0 =1 / 2(1− ξ2 )(1− η) .
В общем виде квадратичные и кубические функции формы для четырехугольного элемента выражаются следующим образом:
для квадратичных элементов |
|
|
угловой узел φl = (1 / 4)(1 + ξl )(1 + ηl ) |
(ξl + ηl −1), |
l = 0, 2, 4, 6 , |
узел в середине стороны φl = (1 / 2)(1 − ξ2 )(1 + ηl ), |
l = 1, 5 , |
|
φl = (1 / 2)(1 + ξl )(1 − η2 ), l = 3, 7 ;
для кубических элементов
угловой узел φl = (1 / 32)(1 + ξl )(1 + ηl )(−10 + 9(ξ2 + η2 )), l = 0, 3, 6, 9 ,
узел в середине вертикальных сторон φl = (9 / 32)(1− ξ2 )(1+ ηl )(1+ 9ξl ), l =1, 2, 7, 8 ,
219
узелвсередине горизонтальныхсторон φl =(9 / 32)(1+ξl )(1−η2 )(1+9ηl ),
l = 4, 5,10,11.
Базисные функции иерархического типа для прямоугольников.
При имеющемся наборе одномерных базисных функций иерархического типа генерирование иерархических базисных функций для прямоугольного элемента не составляет никакой проблемы. Функции для угловых узлов совпадают со стандартными билинейными функциями (4.11). Для неугловых узлов приемлемым оказывается любое произведение одномерной иерархической функции с локальной переменной вдоль стороны элемента, скажем, ξ и линейной (или иерархической) функции от другой локальной переменной, скажем, η . Например, используя одномерные базисные функции (4.7), можно построить следующие базисные функции:
типичный угловой узел
φ3e (ξ, η) = (1 / 4)(1 + ξ)(1+ η) , |
(4.13) |
типичная сторона 2–3
φe2 (2−3) (ξ, η) = (1 / 4)(1 + η)(ξ2 −1),
(4.14)
φ3e (2−3) (ξ,η) = (1 / 6)(1 + η)(ξ3 − ξ),
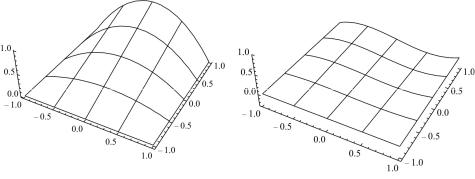
причем этот процесс может быть продолжен до любой степени. Вид этих функций приведен на рис. 4.5.
а |
б |
Рис. 4.5. Базисные функции иерархического типа: а – квадратичная (4.141), б – кубическая (4.142)
220
