
1465
.pdfизменить эффективность текста программы – сделать ее короче, выполнение более быстрым, реализацию метода более простой. Для иллюстрации различных подходов будем вычислять с помощью пакета факториал заданного натурального числа.
1. Предопределение: любому действию, которое требуется выполнить, соответствует специальная функция. Пример – классический научный калькулятор. В нашем случае примером предопределения будет команда
Factorial[9] ---> 362880.
Можно ввести и “9!”.
2. Программирование на основе списков: для вычисления необходимо предварительно составить список целых чисел (для приведенного примера от 1 до 9) и применить к нему операцию перемножения элементов. Создать список натуральных чисел можно с помощью уже известной функции “Table[]”, но существует и более простая в использовании функция создания числовых списков “Range[]”:
Range[9] ---> {1,2,3,4,5,6,7,8,9}
Как применять к некоторому списку те или иные функции, мы рассмотрим позже, а пока приведем только один пример. Отметим, что полученный список хранится в ядре пакета в виде конструкции “List[1,2,3,4,5,6,7,8,9]”, а применение к нему функции перемножения элементов (или другого действия) представляется как замена названия функции “List” на новое, в нашем случае – это имя (функция) “Times”. Для замены названия функции на другое применяется функция “Apply[f,expr]”, где f – новое название функции, применяемое к выражению expr. Итак, создадим функцию
listFact[n_]: =Apply[Times,Range[n]] listFact[9] ---> 362880
3. Рекурсия: идея заключается в том, что сама создаваемая функция выполняет только один оператор, который требуется повторять для решения задачи. То есть код программы сдержит небольшую выполняемую часть и использует результаты своих вычислений, сделанных при других значениях аргументов. Факториал 9 при этом подходе определяется как факториал 8, умноженный на 9:
recurFact[n_]: =n recurFact[n–1]; recurFact[0]=1; recurFact[9] ---> 362880
91
4. Процедурное программирование: используются операторы цикла,
условные операторы и прочее. В качестве примера рассмотрим один из операторов цикла – цикл “Do[expr,iterator]”. Синтаксис этой функции аналогичен синтаксису функции “Table[]”, но операторы цикла, выполняя повторы предписанным образом, не возвращают никакого результата, результаты вычислений можно сохранять в переменных и обращаться к ним после завершения работы цикла. Создадим новую функцию:
loopFact[n_]: =Module[{fact}, fact=1; Do[fact*=i,{i,2,n}]] loopFact[9] ---> 362880
Проверьте, чему будет равно вычисленное выражение loopFact[0], и объясните результат. Отметим, что помимо цикла “Do[]” «Mathematica» дает возможность работать с циклами “For[]” и “While[]”. Здесь на особенностях их использования останавливаться не будем.
Преобразование символьных выражений. Для преобразования символьных выражений используются следующие основные встроенные функции: 1) “Expand[expr]” – раскрытие скобок в выражении, для примера выполните команду “e1=Expand[(x–7)5(2x+3)4(8–x)]”; 2) “Factor[expr]” –
разложение на множители, выполните “e2=Factor[e1]”; 3) для тригонометрических выражений используются специальные функции “TrigExpand[expr]” и “TrigFactor[expr]”; 4) для степенных выражений – “PowerExpand[expr]”; 5) общая функция, служащая для упрощения любых выражений, – это функция “Simplify[expr]”. При использовании функции “FullSimplify[expr]” пакет применяет алгоритмы более глубокого упрощения, в том числе специальных функций, что в ряде случаев позволяет получить более простые конечные выражения.
Стандартные математические функции, реализованные в пакете, – это “Power[x,n]” (возведение x в степень n, которая может быть дробной), тригонометрические функции “Sin[x]”, “Cos[x]”, “Tan[x]”, “Cot[x]”, обратные тригонометрические функции “ArcSin[x]”, “ArcCos[x]”, “ArcTan[x]”, “ArcCot[x]”, логарифмические функции “Log[x]” (натуральный логарифм x), “Log[a,x]” (логарифм x по основанию a), экспонента “Exp[x]”.
Найти производную позволяет функция “D[f[var],var]”, где первый аргумент указывает функцию, а второй переменную, по которой берется производная. Пример: “D[f[x,y],x]” – первая частная производная f по x, “D[f[x,y],x,x]” – вторая частная производная f по x, “D[f[x,y],{x,2}]” – так-
же вторая частная производная по x (после запятой в фигурных скобках
92
указывается любой порядок производной), “D[f[x,y],x,{y,3}]” – первая частная производная по x и третья по y.
Интегрирование реализуется с помощью “Integrate[f[var],var]”, во втором аргументе можно также указать и пределы интегрирования: “{var,a,b}” для определенных интегралов. Численное интегрирование реализуется с помощью функции “NIntegrate[f[var],{var,a,b}]”. При этом необходимо задавать числовые значения всех параметров в подынтегральной функции.
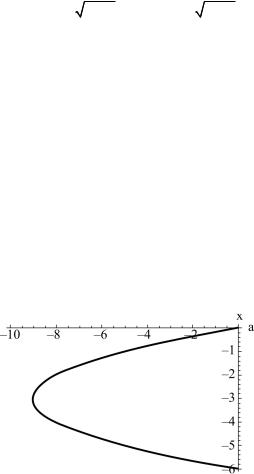
Решение уравнений. Основной функцией для точного решения уравнений является функция “Solve[eqn,x]”, где eqn – уравнение, которое может содержать любые параметры, а x – неизвестная величина. Уравнение в пакете задается с помощью логической операции “==”. Например:
“sol=Solve[x + 6 – a/x == 0, x]” ---> “{{x → − 3− 9+ a},{x→ − 3+ 9+ a}}”.
Как видно, решение представляется в виде подстановок. Полученное в примере решение сохраняется во введенной переменной sol. Для графического исследования поведения корней уравнения в зависимости от параметра a построим график (рис. 1.17):
“Plot[x /. sol, {a, -10, 0}, AxesLabel → {"a", "x"},
PlotStyle → Thick, LabelStyle → {Black, FontFamily → "Times", 16}]”.
Для решения системы уравнений используется та же функция со спи-
ском уравнений и неизвестных: “Solve[{eqn1,eqn2,…},{x1,x2,…}]”. Моди-
фикация этой функции “NSolve[]” дает приближенные значения корней уравнения (примените ее к решению записанного выше уравнения). Читателям предлагается решить точно и приближенно уравнение
“x4 – 2 x3 – x2 – 2 x + 1 == 0”.
Рис. 1.17. Зависимость значений корней x1, x2 уравнения “x + 6 – a/x == 0” от параметра a
93
Отметим, что функции “Solve[]” и “NSolve[]” предназначены для решения полиномиальных уравнений.
Другая функция, позволяющая получить более полное решение ряда уравнений (в том числе некоторых трансцендентных), – это функция с таким же набором аргументов “Reduce[{eqn1,eqn2,…},{x1,x2,…}]”.
Кроме уравнений эта функция позволяет решать и неравенства, в также системы уравнений и неравенств. Дополнительный аргумент позволяет задать поле, над которым будет проведен поиск решения, например:
“Reduce[x4 – 2 x3 – x2 – 2 x + 1 == 0, Reals]”,
где параметр Reals задает поле действительных чисел. Также может вестись поиск решения над полем целых чисел.
Пример решения неравенства (выполнить самостоятельно):
“Reduce[40 + (–18 + p) p ≤ 155,p]”.
Для численного поиска корней трансцендентных уравнений в пакете имеется функция “FindRoot[eqn,{x,x0}]”, которая находит ближайший к x0 корень уравнения eqn. Для нахождения нуля функции вместо уравнения eqn подставляется имя функции f. Эта функция использует метод Ньютона поиска корня. При задании двух начальных значений “{x,x0,x1}” функция будет применять метод секущих. Эта функция может находить и комплексные корни, если задается начальное комплексное значение.
Для точного решения дифференциальных уравнений, как обыкновенных, так и в частных производных, используется модификация “DSolve[]”. Для численного решения дифференциальных уравнений предусмотрена функция “NDSolve[]”, которая допускает выбор метода решения и задания параметров метода. В последующих главах будут рассмотрены примеры использования этих функций при построении дискретных моделей некоторых физико-механических процессов.
Для нахождения минимума функции одного или нескольких аргументов используются функции: 1) “Minimize[f[x1,x2,…],{x1,x2,…}]”, причем дополнительно можно задавать ограничения cons в виде равенств и нера-
венств “Minimize[{f[x1,x2,…], cons},{x1,x2,…}]”, поле dom (Reals, Integers),
над которым ведется поиск решения “Minimize[f[x1,x2,…],{x1,x2,…},
dom]”, 2) “NMinimize[f[x1,x2,…],{x1,x2,…}]”, причем можно также зада-
вать ограничения, выбирать метод численного решения и управлять его па-
94
раметрами, 3) “FindMinimum[f[x1,x2,…],{x1,x2,…}]”, здесь можно зада-
вать метод численного решения, управлять его параметрами, выбирать начальную точку для поиска минимума, задавать ограничения. Отметим, что первая и вторая функции “Minimize[]” и “NMinimize[]”ведут поиск глобального минимума, а функция “FindMinimum[]” ищет локальный минимум. Метод поиска решения задачи минимизации задается опцией “Method→ name”, где name – название метода, принимающее одно из сле-
дующих значений: "Automatic", "Gradient", "ConjugateGradient", "InteriorPoint", "QuasiNewton", "Newton", "LinearProgramming", "QuadraticProgramming", "LevenbergMarquardt", названия которых говорят сами за себя. Значение "Automatic" принято по умолчанию и означает автоматический выбор одного из перечисленных методов в соответствии с некоторым предварительным анализом постановки.
Остальные функции, потребность в которых появится при изложении последующего материала, будут описываться по мере необходимости в других главах пособия.
Список литературы к главе 1
1.Босс В. Интуиция и математика. – М.: КомКнига. 2007. – 192 с.
2.Введение в математическое моделирование/ В.Н. Ашихмин [и др.]; под ред. П.В. Трусова. – М.: Логос, 2005. – 440 с.
3.Воробьев Е.М. Введение в систему «Математика»: учеб. пособие. – М.: Финансы и статистика, 1998. – 262 с.
4.Гольдштейн Р.В., Городцов В.А. Механика сплошных сред. Ч. 1. Основы и классические модели жидкостей. – М.: Наука. Физматлит, 2000. –
256с.
5.Димитриенко Ю.И. Нелинейная механика сплошной среды. – М.:
Физматлит, 2009. – 624 с.
6.Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы. – М.: Мир, 1974. – 304 с.
7.Жилин П.А. Векторы и тензоры второго ранга в трехмерном пространстве. – СПб.: Нестор. 2001. 276 с.
8.Жилин П.А. Актуальные проблемы механики // Актуальные проблемы механики: материалы междунар. летней школы-конфе- ренции. Т. 1. Институт проблем машиноведения РАН. – СПб., 2006. –
306 с.
95
9. Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложения. – М.: Наука.
1986. – 232 с.
10.Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. – М.: Мир, 2002. – 461 с.
11.Седов Л.И. Механика сплошной среды: в 2 т. Т. 1. – СПб.: Лань,
2004. – 528 с.
12. Седов Л.И. Механика сплошной среды: в 2 т. Т. 2. – СПб.: Лань, 2004. – 560 с.
13. Трусделл К. Первоначальный курс рациональной механики сплошных сред. – М.: Мир, 1975. – 592 с.
96
ГЛАВА 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ДЕФОРМИРУЕМЫХ ТВЕРДЫХ ТЕЛ НА АТОМАРНОМ УРОВНЕ. ДИСКРЕТНЫЙ ПОДХОД
В связи с интенсивным развитием вычислительной техники расширяются возможности дискретных подходов описания механического поведения твердых тел, в том числе их неупругого деформирования и разрушения [6–7]. Одним из таких подходов является метод молекулярной динамики/статики, позволяющий с помощью задания потенциала межатомного взаимодействия описывать различные физикомеханические эффекты, сопровождающие деформирование твердых тел. В частности, при анализе упругого поведения твердого тела дискретный подход позволяет провести численный эксперимент по установлению особенностей упругого отклика. Например, оценить его линейность/нелинейность по отношению к накладываемым деформациям, исследовать симметрийные, анизотропные свойства упругого закона, определить зависимость упругих модулей от размеров тела (в том числе для тел микро- и наномасштабов). Полученные зависимости могут использоваться в многоуровневых упругопластических моделях деформирования твердых тел, например металлических поликристаллов, мезоуровень которых отождествляется с отдельным зерном или фрагментом, в микро- и наномеханике, для уточнения моделей, используемых в механике микронеоднородных (композиционных) материалов.
Межчастичные потенциалы в дискретном подходе являются приближенным способом описания силового взаимодействия частиц материала, качественно отражающим основные свойства атомов отталкиваться на малых расстояниях, притягиваться при увеличении расстояния и «не чувствовать» друг друга на больших расстояниях. Получаемые количественные результаты зависят от числовых значений параметров потенциалов. В настоящее время не существует единых методик определения этих параметров для произвольных материалов.
97
2.1. ИСТОРИЯ ДИСКРЕТНОГО ПОДХОДА. МЕТОД МОЛЕКУЛЯРНОЙ ДИНАМИКИ. СРАВНЕНИЕ РАЗЛИЧНЫХ ПОТЕНЦИАЛОВ. ЧИСЛЕННЫЕ МЕТОДЫ
Одним из способов теоретического исследования термомеханических свойств конденсированных сред является дискретный подход, основанный на прямом моделировании движения частиц, вызванного их взаимодействием и приложенными внешними воздействиями. История дискретного подхода в статической постановке начинается в 1827 году с работ Клода Луи Мари Анри Навье (1785–1836) и Огюстена Луи Коши (1789–1857) об определении структуры линейного упругого закона и числа независимых упругих модулей. Навье вывел уравнение равновесия упругих тел, исходя из предположения, что идеальное упругое тело состоит из молекул, между которыми возникают силы взаимодействия. При выводе он принимал, что силы взаимодействия направлены по прямым, соединяющим частицы тела, и пропорциональны расстояниям между ними (первое приближение для потенциала межатомного взаимодействия). Для изотропных тел его уравнения содержали только одну упругую постоянную. Примерно в то же время и Коши исследовал строение упругого закона. Он изначально ввел два упругих модуля для изотропного материала. В самом общем случае принимал, что каждая из 6 компонент тензора напряжений является однородной линейной функцией от 6 компонент тензора деформаций, то есть для описания упругого поведения твердого тела необходимо не более 36 упругих постоянных. Принимая молекулярную теорию, Коши снизил число упругих постоянных в обобщенном законе Гука с 36 до 15. В изотропном случае он получил, как и Навье, только одну упругую постоянную. Молекулярной теории при анализе упругих свойств материалов придерживался и Симеон Дени Пуассон (1781–1840). В 1829 году он опубликовал работу, в которой на основе молекулярной теории показал, что при простом растяжении стержня осевое удлинение сопровождается поперечным сужением на величину ν = 1 / 4 . И если E ― модуль Юнга, то модульG вопытенапростойсдвигизотропногоматериаладолженбытьравен:
G = |
|
E |
= 0, 4 E . |
|
+ 1 / 4) |
||
2(1 |
|
||
Проведенные впоследствии эксперименты показали результаты, расходящиеся с представлениями одноконстантной теории. Хотя всегда оставалось сомнение, что испытуемый материал в действительности является изотропным. Поэтому представление о возможности полностью оце-
98
нить упругие свойства изотропного тела одной упругой постоянной на ранних стадиях развития теории упругости пользовалось всеобщим признанием (Навье, Коши, Пуассон, Ламе, Клапейрон…).
Изменения были внесены Джорджем Грином (1793–1841), который предложил вывод уравнений теории упругости без использования какой бы то ни было гипотезы о строении тел. Главный вклад в развитие теории упругости им был сделан в работе «О законах отражения и преломления света на поверхности раздела двух некристаллических сред». В этой статье им был сформулирован следующий принцип: «Каким бы образом элементы материальной системы ни действовали друг на друга, полная сумма произведений внутренних сил на элементы тех направлений, вдоль которых они действуют, для каждой заданной части массы должна быть всегда равна полному дифференциалу некоторой функции». Тем самым он внес в теорию упругости понятие потенциала. Грин также показал, что в предположении малых перемещений потенциал является однородной функцией второй степени от шести компонент деформаций. В самом общем случае она содержит 21 постоянную. Эти постоянные полностью определяют упругие свойства материала. Для изотропного тела остаются две упругие постоянные.
Работа Грина явилась отправным пунктом долгой дискуссии о количестве упругих модулей и привела к формированию двух школ в теории упругости: «упругость по Коши», «упругость по Грину». Таким образом, первое противопоставление дискретного и непрерывного подхода возникло со спора о количестве упругих постоянных для изотропной линейно упругой среды.
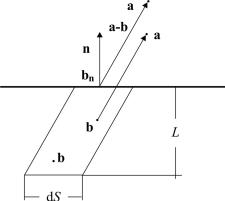
Рис. 2.1. Цилиндр для определения напряжений Коши в упругом теле
Рассмотрим основные идеи, которым следовали Навье, Коши, Пуассон при выводе упругого закона из представлений о дискретном строении вещества. Чтобы найти тензор напряжений Коши, рассмотрим упругое пространство с мысленным разрезом, на поверхности которого выделена бесконечно малая материальная площадка n dS с нормалью n.
Построим на этой площадке в направлении, противоположном n, цилиндр высотой l, которая превыша-
99

ет расстояние, на котором еще существенно взаимодействие между парой частиц (рис. 2.1). Вектор напряжений на площадке n dS вызван си-
лами, действующими на частицы с радиусом-вектором b цилиндра со стороны всех частиц с радиусом-вектором a из «положительного» (см. рис. 2.1) полупространства.
Принимаются следующие предположения:
1. В результате деформирования из начальной ненапряженной конфигурации частицы a и b перемещаются в положения a' и b'. Поле вектора перемещений u(x) будем считать непрерывным однозначным на всем упругом пространстве. Тогда
a ' = a + u(a) , b ' = b + u(b) , a '− b ' = a − b + u(a) − u(b) = a − b + uab . (2.1)
Значения вектора перемещений u(a) и u(b) определены для точек
упругого континуума, в которые попадают рассматриваемые частицы. 2. Предположим, что сила парного взаимодействия fab между части-
цами a и b направлена по линии a '− b ', а ее величина зависит от расстояния между частицами и пропорциональна их массам ma , mb :
fab = mamb f ( |
|
a '− b ' |
|
) (a '− b ') / |
|
a '− b ' |
|
. |
(2.2) |
|
|
|
|
3. Функцию f (r) будем считать непрерывной вместе со всеми производными любого порядка.
4.Функция f (r) с ростом расстояния r настолько быстро стремится
кнулю, что в рассмотрении остаются значения f (r) только для беско-
нечно малых r.
5. Принимается, что накладываемое поле перемещений соответствует однородному полю линейного тензора малых деформаций ε без поворотов материальных объемов, поэтому u(r) = ε r , то есть
a '− b ' = r (a− b)= (I+ ε) (a− b) . |
(2.3) |
Относительное изменение расстояния между частицами a '− b ' / a − b равно
λ = |
|
a−' b ' |
|
/ |
|
a− b |
|
= ε: mm , |
(2.4) |
|
|
|
|
где единичный вектор m = (a − b) / a − b , аналогично, m ' = (a '− b ') / a '− b ' . Предположения 4 и 5 позволяют линеаризовать функцию f (r) :
100
