1465

Следует отметить, что при использовании иерархических элементов добавление многочленных компонент очень легко осуществить локально, чтобы добиться уточнения в области, где неизвестная функция изменяется особенно быстро и, следовательно, аппроксимация может давать наибольшие погрешности.

Двумерные базисные функции для треугольников. L-координаты.

Треугольные элементы часто называют симплексами, поскольку это простейшая плоская фигура, которой можно покрыть без разрывов и наложений плоскую область.

Кроме того, если рассмотреть семейство треугольников произвольного вида при условии, что узлы располагаются в точках пересечения семейства прямых, проведенных параллельно сторонам треугольника, то каждый раз число таких узлов оказывается достаточным, чтобы построить семейство полных многочленов (рис. 4.6).

Рис. 4.6. Семейство треугольных элементов: а – треугольник Паскаля;

б– элемент первого порядка; в – элемент второго порядка;

г– элемент третьего порядка

Рассмотрим построение двумерного линейного треугольного элемента. Линейный треугольный элемент содержит три узла i, j, и k, расположенных в вершинах треугольника, перенумерованных против часовой стрелки (рис. 4.7). Координаты узлов в системе координат хОу: (xi, yi), (xj, yj), (xk, yk) соответственно. Функции формы для каждого узла записываются в виде

221

узлавычисляются изусловия, чтовсвоем узле базисная функция равна 1 в остальных узлах – 0. Тогда для i-го узла получим СЛАУ относительно неизвестных коэффициентов:

Таким образом

222

Для определения неизвестных шести констант необходимо решить СЛАУ из шести уравнений, полученных из условия равенства базисной функции 1 в своем узле и равенства нулю в остальных узлах:

Аналогичные системы уравнений необходимо решить для определения функций форм оставшихся пяти узлов. Однако такой способ построения для функций формы высших степеней не очень удобен. Рассмотрим более простой способ, основанный на использовании локальной системы координат.

Запишем линейную зависимость между локальными координатами L1, L2, L3 и декартовыми координатами произвольной точки внутри треугольника:

Здесь (xi, yi), (xj, yj), (xk, yk) – декартовы координаты вершин треугольника. Очевидно, что функция L1 должна принимать значение 1 в i-м узле и обращается в 0 в остальных вершинах – совершенно так же, как базисные функции линейного треугольного элемента.

Несложно показать, что L1 выражаются через координаты вершин треугольника в виде соотношений

223

1 xi yi

где ∆ = 1 x j y j = 2S∆ .

1 xk yk

Аналогично для L2, L3.

Линии уровня этой функции L1 = const параллельны стороне треугольника, противоположной узлу i. Можно показать, что

соотношениями (4.15)–(4.19).

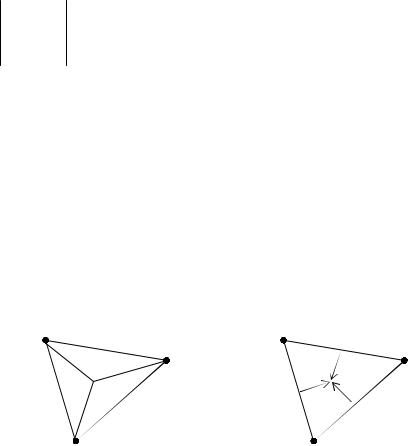
L-координаты любой точки внутри треугольника могут быть вычислены как отношение площадей (рис. 4.9):

Рис. 4.9. Локальные L-координаты в треугольном элементе

Из геометрических соображений очевидно, что

Общий вид функции формы высших порядков для треугольного элемента в L-координатах задается выражением

где n – порядок треугольного элемента (число узлов на стороне –1); Fδ = Li − c – функция L-координат, определяется из уравнений n линий

224

уровня функций L1, L2, L3, которые проходят через все узлы, за исключением узла, для которого определяется функция формы; Fδ(L1, L2 , L3 ) – значение

этих функций в узле, для которого составляется функция формы. Соотношение(4.25) являетсяполиномом Лагранжа, записанного вL-координатах.

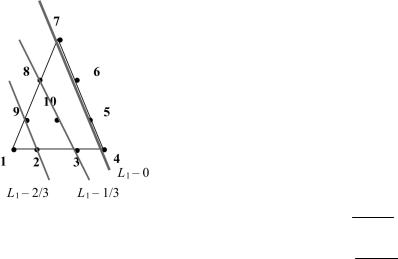
Пример. Составить функцию формы для 1-го узла кубического элемента.

Вычислим значения этих функций для 1-го узла, имеющего L-коор-

динаты (1, 0, 0):

F1 (1, 0, 0) =1,

F2 (1, 0, 0) = 2 / 3,

F3 (1, 0, 0) =1 / 3.

Окончательно получаем базисную функцию для 1-го узла:

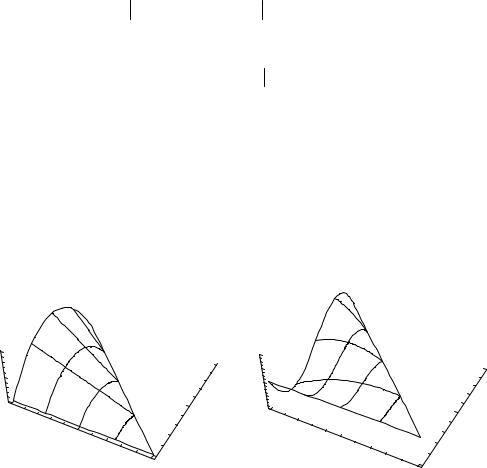
На рис. 4.11 показаны типичные базисные функции для линейных, квадратичных и кубических треугольных элементов.

В[9] приведены выражения для всех функций форм квадратичных

икубических треугольных элементов.

225

0.5

1.0 0.0

а

1.0

0.5

0.0

1.0

1.0

0.5

0.5

0.00.0

б

в

Рис. 4.11. Базисные функции на треугольном элементе:

а– линейный, б – квадратичные, в – кубические

В[3] приводится вид иерархических базисных функций для треугольников, записанные в L-координатах. Например, для стороны треугольника j–k их можно записать по аналогии с соотношениями (4.8) в виде

226

Такой вид соотношений можно объяснить следующим образом: поскольку L1 вдоль стороны j–k тождественно равно нулю и в силу (4.213)

[L2 + L3]j-k = 1;

если ξ – обычная безразмерная локальная координата элемента типа использовавшейся для построения иерархических базисных функций для одномерныхэлементов, измеряемаявдольстороныj–k, томожнозаписать

L2 j−k = −(ξ−1) / 2, L3 j−k = (ξ+1) / 2 .

Тогда можно положить

ξ = (L3 − L2 ) j −k .

Отметим, что для построения базисных функций степени выше 2 набора иерархических функций, соответствующих узлам на сторонах элемента, недостаточно для определения полного многочлена и требуются внутренние иерархические функции, тождественно равные нулю на границах элемента. Например, для кубической аппроксимации можно использовать функцию L1L2L3, а для аппроксимации четвертой степени можно ввести три дополнительных функции L12 L2 L3 , L1L22 L3 , L1L2 L23 .

На рис. 4.12 показаны типичные иерархические квадратичная и кубическая базисные функции.

Рис. 4.12. Иерархические функции формы на треугольном КЭ: а – квадратичная; б – кубическая

227

Отметим еще одно преимущество L-координат – использование интегральных формул для интегрирования по объему и границе конечного элемента.

Например, можно вычислить интеграл от произведения базисных функций:

4.2.3. Трехмерные базисные функции

Рассмотренные выше способы построения одномерных и двумерных базисных функций можно обобщить для трехмерных элементов в виде параллелепипедов и тетраэдров.

Например, используя трехмерные нормированные координаты ( −1 ≤ ξ, η, ζ≤ 1), можно записать следующие формы для элементов в виде

прямоугольных параллелепипедов серендипова семейства [3]: Элемент первого порядка (8 узлов)

φl = (1 / 8)(1 + ξ%l )(1 + η%l )(1 + ζ%l ) .

Элемент второго порядка (20 узлов): угловые узлы

φl = (1 / 8)(1 + ξ%l )(1 + η%l )(1 + ζ%l )(ξ%l + η%l + ζ%l − 2) ;

узел на ребре

ξl = 0, ηl = ±1, ζl = ±1,

φl = (1 / 4)(1 − ξ2 )(1+ η%l )(1+ ζ%l ) .

Элемент третьего порядка (32 узла): угловой узел

φl = (1 / 64)(1 + ξ%l )(1 + η%l )(1 + ζ%l )(9(ξ2 + η2 + ζ2 ) −19) ;

узел на ребре

φl = (9 / 64)(1 − ξ2 )(1 + 9ξ%l )(1 + η%l )(1 + ζ%l ) .

228

Функции формы степени p лагранжева семейства для прямоугольных параллелепипедов в локальной нормированной системе координат ( −1 ≤ ξ, η, ζ≤ 1) могут быть записаны как обобщение на трехмерный слу-

чай соотношений (4.12):

φersq (ξ, η, ζ) = Λ rp (ξΛ) sp (Λη) qp (ζ) .

Аналогично плоским треугольным элементам можно построить тетраэдрические элементы, функции формы которых записываются в пространственных L-координатах. Аналогично соотношению (4.21) запишем линейную зависимость между локальными координатами L1, L2, L3, L4 и декартовыми координатами произвольной точки Р внутри треугольника:

x = L1xi + L2 x j + L3 xk + L4 xl , x = L1 yi + L2 y j + L3 yk + L4 yl , 1 = L1 + L2 + L3 + L4 .

Здесь (xi, yi), (xj, yj), (xk, yk), (xl, yl) – декартовы координаты вершин тетраэдра. Очевидно, что функция L1 должна принимать значение 1 в i-м узле и обращается в 0 в остальных вершинах – совершенно так же, как базисные функции линейного тетраэдрального элемента. Можно показать, что

φi = L1, φj = L2 , φk = L3 , φl = L4 .

L-координаты любой точки Р внутри треугольника могут быть вычислены как отношение объема тетраэдра с вершиной в этой точке к объему всего тетраэдра (рис. 4.13):

229

4.2.4. Разбиение области на элементы. Требования к конечным элементам

Дискретизация области. Процесс дискретизации можно разделить на два этапа: разбиение расчетной области на элементы и нумерация элементов и узлов. Сложности второго этапа связаны с требованиями повышения эффективности вычислений [9].

Рассмотрим принципы разбиения двумерной области на линейные треугольные элементы. Двумерная область выбрана для удобства иллюстрации, но идеи, представленные здесь, легко обобщить на трехмерный случай. Линейный треугольник выбран потому, что это простейший из двумерных элементов в смысле аналитической формулировки.

При разбиении любой двумерной области сначала область делится на четырехугольные или треугольные подобласти, которые затем подразделяются на треугольники. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала.

Наиболее просто разбить треугольную подобласть на элементы, если выбрать определенное число узлов вдоль каждой стороны, соединить соответствующие узлы прямыми линиями и точки пересечения этих линий считать узлами (рис. 4.14). Узлы на сторонах подобласти необязательно располагать на равных расстояниях. Варьирование расстояния между ними позволяет изменять размеры элементов. Если треугольная подобласть криволинейная, то криволинейные границы элементов заменяются на прямые отрезки. Если на стороне треугольной подобласти выбрано п узлов, число треугольных элементов в результате разбиения равно (п – 1)2.

Четырехугольные зоны обычно разбиваются на элементы соединением узлов на противоположных сторонах. Пересечения линий определяют внутренние узловые точки (рис. 4.15). Внутренние четырехугольники могут рассматриваться как элементы; но они могут быть разбиты и на треугольные

230