2.5.Динамика колебательного движения.

Уравнение динамики гармонического колебания найдём решая прямую задачу: по заданному закону движения 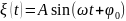, определить действующую силу. Здесь A – амплитуда, - начальная фаза. Следуя определённому выше алгоритму, найдём скорость и ускорение маятника:

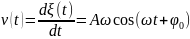
- гармоническая функция

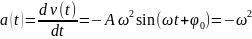ξ

Так как 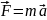, то = - - решение задачи. Сила, пропорциональная смещению и направленная в сторону противоположную ему, вызывает колебательное движение.

Утверждение, что уравнение движения задано, предполагает заданными величины: A, , (или необходимо задавать начальные условия).

Тогда силу можно записать в явном виде: F(t)=– .

Уравнение колебаний в канонической форме

Выведем на примере пружинного маятника.

равновесия.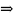

– динамическое уравнение колебаний

в каноническом виде. Где - постоянная величина, характеризующая

свойства системы ( ). В нашем случае,

Решение уравнения вида: есть гармоническая

функция Постоянные –- функции начальных условий.

Полное начальное условие: t = 0, .

Пример: пусть при t = 0. 0. :

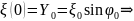две неизвестные величины: Воспользуемся вторым условием

. Тогда . ox

Найдем каноническое уравнение математического маятника: x

- каноническое уравнение математического маятника.

Его решение известно

X(t)= . где ; - из начальных условий.

Физический маятник - твёрдое тело, имеющее ось вращения.

Запишем уравнение моментов: , .

Найдём момент силы относительно точки подвеса:

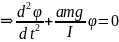– дифференциальное уравнение в каноническом виде.

. Уравнение колебаний: Sin(

2.6.Динамика волнового движения. Волновое уравнение. Кинематическое уравнение волны: –волна распространяется в положительном направлении Ox. – в отрицательном направлении оси OX.

Таким образом, Продифференцируем дважды и приравняем вторые производные:

=

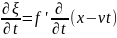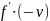
– волновое уравнение в канонической форме, где C – характеризует упругие свойства среды и свойства колебательной системы.

`Итак, получены уравнения динамики основных механических систем в виде дифференциальных уравнений второго порядка

движение материальной точки или поступательное твёрдого тела.

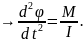; вращательное движение твёрдого тела относительно точки (оси)

вместе сложное движение твёрдого тела

-уравнение колебаний в канонической форме

– волновое уравнение в канонической форме.

Раздел 3. Движение в неинерциальных системах отсчета

Поступательные и центробежные силы инерции. Силы инерции в общем случае. Сила Кориолиса.

Постановка задачи. В предыдущих разделах были рассмотрены Механические системы, движение которых описывалось относительно условно неподвижных тел (систем) отсчёта. В качестве параметра, определяющего различные типы движений, было выбрано ускорение. Такое описание оказалось чрезвычайно полезным, поскольку ускорение при динамическом описании связано непосредственно с причиной изменения состояния движения – силой. В таких системах отсчёта (названных инерциальными) работают основные законы механики, что позволяет сформулировать разнообразные математические модели механических систем. Для решения ряда практических задач часто требуется рассмотрение движения МС относительно подвижных тел (систем) отсчёта.

П усть имеем одно тело отсчёта условно неподвижное и второе, которое может двигаться относительно первого. Векторную систему отсчёта S свяжем с первым телом, систему отсчёта с подвижным телом отсчёта. В качестве исследуемой МС возьмём простейшую - материальную точку. Полагаем далее, что движение нерелятивистское т.е. время в системах одинаковое, массы постоянные, расстоянию между двумя точками одинаково в S и . Положение начала подвижной системы относительно S задаётся радиус-вектором 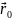, положение точки соответственно (t) и (t).

По правилам векторного сложения имеем: (t) = (t). (1)

Продифференцируем по времени: (2)

Соотношение (2) представляет правило сложения скоростей Галилея.

1. Пусть система движется с постоянной скоростью. Тогда обе системы инерциальные. Ускорения:

и законы механики - одинаковы.

2. Система движется с ускорением, тогда и Соответственно законы механики в системах S и имеют различный вид.

В системе S : m . В системе _отн= --m _пер

Подвижная система неинерциальная. Законы движения механических систем принимаю другой вид.

Выполнение законов в них требует, кроме сил, действующих со стороны других тел (F), добавления других сил, связанных с ускоренным движением системы отсчёта.

Силы, действие которых связано с ускоренным движением системы отсчета – силы инерции.

Свойства сил инерции:

1. Эти силы отсутствуют в инерциальных системах отсчёта.

2. Мы не можем указать конкретное тело, со стороны которого действуют силы инерции.

3. Силы инерции остаются пропорциональны массе тел.

4. Ели силы инерции действуют на систему тел, то они внешние

5. Если на систему тел действуют силы инерции, то в ней не выполняются законы сохранения энергии, импульса, момента импульса в традиционной форме. Т.е. движение под действием сил инерции эквивалентно движению во внешних силовых поля.

= – m Это сила инерции поступательного движения.

3. Пусть система S’ вращается вокруг неподвижной оси с угловой скоростью ,. Тогда

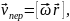
Если скорость вращения постоянна то и =

. Тогда на неподвижное тело в этой системе также будет действовать сила инерции, которую можно найти по общему правилу: = –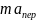 = – m = –m r– это центробежная сила инерции. Она направлена по радиусу от оси вращения.

4. Рассмотрим более общий случай. Пусть система движется поступательно со скоростью и вращается с угловой скоростью вокруг неподвижной оси ( т.е движется произвольно). Тогда по принципу суперпозиции движения полная скорость системы: -это составляющая вектора скорости, связанная с вращением. Пусть далее, все параметры движения (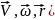 есть функции времени. По правилу сложения векторов ускорений:

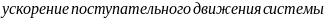, . Порождает поступательную силу инерции = – m

Рассмотрим слагаемое , где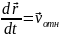 - скорость движения тела m, относительно системы S’. ускорение, связанное с неравномерностью вращение системы. При -это ускорение, связанное с изменением радиус-вектора точки по направлению =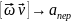 = = r- нормальное ускорение

И ускорения, связанного с изменением скорости за счёт изменением радиуса-вектора точки по величине, при движении вдоль радиус –вектора. Это ускорение Кориолиса.

Тогда =

Сила инерции = – m -также состоит из двух составляющих: центробежной силы инерции, связанной только с вращением тела (с изменением радиуса-вектора точки по направлению) и силы инерции Кориолиса, связанной с движением тела, относительно подвижной системы (с).

Теорема Кориолиса.

Абсолютное ускорение тела есть векторная сумма ускорений: относительного, переносного и Кориолиса.

Здесь

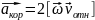
То есть .

S’: - m закон динамики тела в S'.

= – 2m[ ], сила перпендикулярна к веторам скоростей.