1.5.7. Теорема Пуассона

В теореме Бернулли устанавливается связь между относительной частотой появлений события и его вероятностью Р при условии, что последняя от опыта к опыту не изменяется. Другими словами, теорема Бернулли справедлива и при проведении опытов в неизменных условиях.

Оказывается, аналогичная связь существует и при переменных условиях опыта, т.е. когда вероятность от опыта к опыту меняется. Теорема, в которой устанавливается связь между относительной частотой появления события и некоторой постоянной величиной при переменных условиях опыта, называется теоремой Пуассона.

Теорема Пуассона. Если производится n независимых опытов и вероятность появления события А в i-м опыте равна P_i, то при увеличении n относительная частота появления события m/n сходится по вероятности к среднему арифметическому значению вероятностей P_i, т.е.

(1.133)

Доказательство. Пусть произведено n независимых опытов с вероятностью появления события А в i-м опыте P_i. Обозначим число появлений события А в i-м опыте через X_i (i=1, 2, 3, …, n).

Очевидно , общее число появлений события А в n опытах:

(1.134)

а относительная частота

(1.135)

Определим математическое ожидание и дисперсию относительной частоты появления события А:

(1.136)

поскольку ряд распределения для X_i имеет вид:

Xi	0	1
Pi	qi	pi

где ;

(1.137)

поскольку

(1.138)

Итак,

(1.139)

. (1.140)

Применяя неравенство Чебышева (1.110) для случайной величины m/n, получим

(1.141)

а учитывая равенство (1.140), будем иметь:

(1.142)

Каким бы ни было число ε, при n→∞ величина дроби , а вероятность .

1.6. Проверка статистических гипотез

При разработке планов статистического контроля и регулирования качества, а также при статистическом анализе полученных результатов приходится решать задачи сравнения. Например, сравнение точности работы станка или измерительной системы со стандартом, сравнение качества нескольких станков и т.д. Для решения этих задач по данным выборочных наблюдений используются статистические критерии, т.е. методы статистической проверки гипотез. Рассмотрим некоторые общие положения.

Статистической гипотезой называют любое предположение о виде или параметрах неизвестного закона распределения.

Сопоставление высказанной гипотезы относительно генеральной совокупности с имеющимися выборочными данными, сопровождаемое количественной оценкой степени достоверности получаемого вывода и осуществляемое с помощью того или иного статистического критерия, называется проверкой статистических гипотез.

Нулевой гипотезой (Н₀) называют выдвинутую гипотезу, которую нужно проверить, а гипотезу (Н₁), противоположную нулевой, называют конкурирующей.

Проверка статистических гипотез осуществляется с помощью статистического критерия (К), который является функцией от результатов наблюдения.

Под статистическим критерием (К) понимают однозначно определенное правило, устанавливающее условия, при которых проверяемую гипотезу (Н₀) по результатам наблюдений следует либо отвергнуть, либо не отвергнуть. Основу критерия составляет специально составленная выборочная характеристика (статистика) Q_n^*=Q_n^*(x₁, x₂, ..., x_n), точное или приближенное распределение которой известно, где x₁, x₂, ..., x_n — выборочные наблюдения.

Каждый критерий разбивает все множество возможных значений ста­тистики на две непересекающиеся области: критическую область и область принятия гипотезы. Если наблюдаемое значение статистики критерия попадает в критическую область, то гипотезу (Н₀) отвергают. В противном случае гипотезу не отвергают. При использовании статистического, критерия возможны четыре случая:

• гипотеза Н₀ верна и ее принимают согласно критерию;

• гипотеза Н₀ неверна и ее отвергают согласно критерию;

• гипотеза Н₀ верна, но ее отвергают согласно критерию (ошибка первого рода);

• гипотеза Н₀ неверна, но ее принимают согласно критерию (ошибка второго рода).

Значение критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия К_набл.

Значения критерия, разделяющие совокупность значений критерия на область допустимых значений и критическую область, определяемые на заданном уровне значимости α по таблицам распределения случайной величины К, выбранной в качестве критерия, называют критическими точками К_кр.

Статистический критерий не дает логического доказательства или опровержения гипотезы. Так как гипотеза (Н₀) проверяется по результатам выборочных наблюдений, то неизбежно имеет место некоторая, хотя бы и очень малая, вероятность ошибочного решения как первого, так и второго рода. При неограниченном увеличении объема выборки и использовании обоснованного критерия, возможно, добиться как угодно малых вероятностей обеих ошибок. Однако наиболее часто в практических задачах контроля имеют дело с фиксированным объемом выборки, когда задаются вероятностью ошибки первого рода — так называемым уровнем значимости α.

Выбор уровня значимости α зависит от сопоставления потерь, связанных с ошибками первого и второго рода. Следует учитывать, что уменьшение α приводит к росту вероятности ошибки второго рода. Поскольку в большинстве практических задач определить величину потерь оказывается весьма затруднительно, то, как правило, пользуются некоторыми стандартными уровнями значимости. К таким значениям можно отнести: α=0,1; 0,05; 0,01; 0,005; 0,001. Наиболее часто используют значение α=0,05, которое означает, что в среднем в 5 случаях из ста мы можем допустить ошибку и отвергнуть гипотезу Н₀, в то время как она справедлива.

В небольшой доле случаев нулевая гипотеза принимается, в то время как на самом деле она ошибочна. Вероятность ошибки второго рода - β. Вероятность 1-β называют мощностью критерия.

Под мощностью критерия понимают вероятность того, что нулевая гипотеза (Н₀) будет отвергнута, если верна конкурирующая (H₁) гипотеза, т.е. вероятность (1—β) не допустить ошибку второго рода.

Результаты решения относительно нулевой гипотезы представлены в табл. 1.

Таблица 1

Нулевая гипотеза Н0	Результаты решения относительно Н0
	Отклонена	Принята
Верна	Ошибка 1-го рода, ее вероятность Р(Н1/Н0)=α	Правильное решение, его вероятность Р(Н0/Н0)=1-α
Неверна	Правильное решение, его вероятность Р(Н1/Н1)=1-β	Ошибка 2-го рода, ее вероятность Р(Н0/Н1)=β

С целью обеспечения максимума мощности критерия в зависимости от гипотезы Н₁ выбирают правостороннюю, левостороннюю или двустороннюю критические области. Границы критической области при заданном уровне значимости α находят из соотношений:

— для правосторонней критической области (рис. 10 а)

; (1.143)

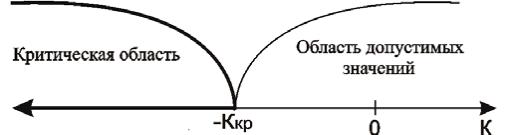
— для левосторонней критической области (рис. 10 б)

; (1.144)

— для двусторонней симметричной области (рис. 10 в)

; (1.145)

, (1.146)

где Q_кр^’ — левосторонняя, a Q_кр^’’ — правосторонняя границы критической области.

Основной принцип проверки статистических гипотез состоит в следующем:

- если наблюдаемое значение критерия принадлежит критической области, то нулевая гипотеза отклоняется в пользу конкурирующей;

- если наблюдаемое значение критерия принадлежит области допустимых значений, то нулевую гипотезу нельзя отклонить.

а)

б)

в)

Рис. 10. Границы критических областей

Статистические критерии позволяют либо отвергнуть гипотезу (высказанная гипотеза противоречит данным наблюдений), либо не отвергнуть (гипотеза не противоречит данным наблюдений, а потому ее можно принять в качестве одного из допустимых решений). При этом неотрицательный результат не означает, что наше предположение (гипотеза) является единственно подходящим. Поэтому статистически проверенную гипотезу следует рассматривать как достаточно правдоподобное, не противоречащее опыту утверждение.