3.3. Планирование экспериментов

Для сокращения числа имитационных экспериментов (расчетов на ЭВМ) при сохранении заданной точности в последнее время находят все более широкое применение методы теории оптимального планирования эксперимента. Планирование эксперимента в задачах моделирования состоит в выборе логической структуры искусственного эксперимента на ЭВМ и позволяет обоснованно проводить выбор значений управляемых параметров для выполнения расчетов на модели.

В планировании экспериментов для описания результирующей характеристики (в нашем случае - критерия оптимальности) используют полиномиальные модели, аппроксимирующие реальный вид целевой функции:

Эта функция в планировании экспериментов называется функцией отклика или уравнением регрессии, пространство, в котором строится функция отклика, - факторным пространством (рис. 28). Коэффициенты функции отклика b₀, b_i, b_ij, b_ii и т.п. можно интерпретировать как значения частных производных в точке, вокруг которой производится разложение в ряд неизвестной целевой функции.

Для поиска оптимума в области определения факторов выбирают произвольную точку А₁. В окрестности точки А₁ выделяют малую подобласть, в которой возможно описать функцию отклика полиномом первой степени (рис. 28). В этой подобласти осуществляют небольшую серию экспериментов (точки I), необходимую для построения линейной модели:

Коэффициенты регрессии b_i используются для определения направления градиента, следуя которому осуществляют дальнейшие опыты (точки II в окрестности точки А₂). Для каждой новой подобласти вновь определяют направление градиента, по которому следуют в дальнейших опытах до тех пор, пока не достигнут оптимума - области М.

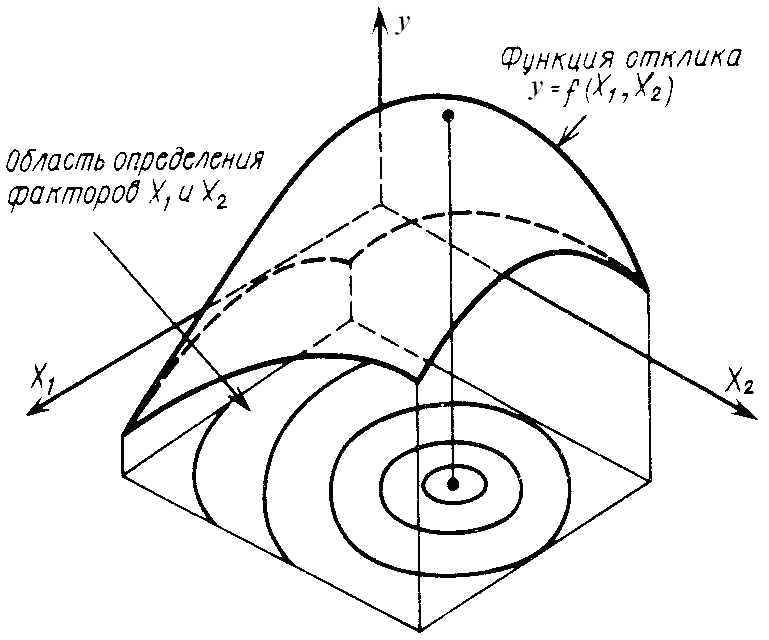
Рис. 27. Функция отклика и факторное пространство

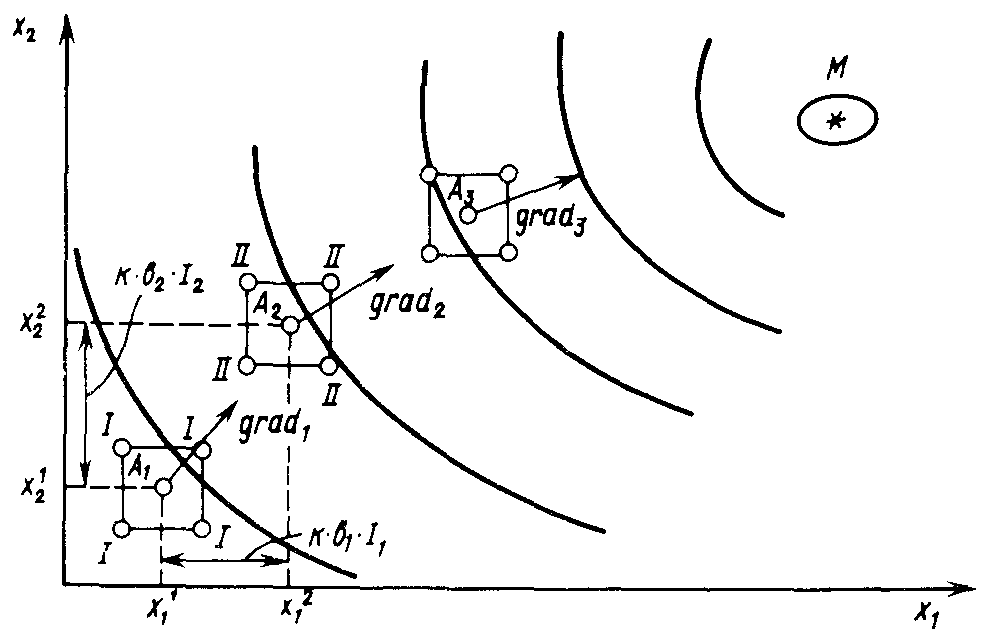
Рис. 28. Планирование имитационных экспериментов при оптимизации по градиенту

Значения коэффициентов регрессии определяются по формуле

где xm_i - значение j-го фактора в m-м эксперименте; y_m - значение выходной характеристики в m-м эксперименте; N - общее число экспериментов в подобласти.

Информацию дня проведения эксперимента записывают в матрице планирования эксперимента (табл. 16), называемой планом эксперимента.

Таблица 16

Матрица планирования эксперимента

№ опыта	Значения факторов					Значение результата
	x1	…	xi	…	xn
1	x11	…	x1i	…	x1n	y1
…	…	…	…	…	…	…
m	xm1	…	xmi	…	xmn	ym
…	…	…	…	…	…	…
N	xN1	…	xNi	…	xNn	yN

Для получения коэффициентов регрессии b_i с высокой точностью и достоверностью к плану эксперимента предъявляется ряд требований, что приводит к формированию значений xm_i. по специальным правилам.

Процедура выбора подобласти проведения эксперимента состоит из двух этапов: выбор основного уровня х_0i и выбор интервалов варьирования I_i. Основной уровень - центр подобласти проведения эксперимента - для первого эксперимента осуществляется эвристически на базе анализа априорной информации. В дальнейшем его величина определяется направлением градиента и шагом эксперимента.

Интервалом варьирования I_i фактора х_i называется некоторое число, прибавление которого к основному уровню дает верхний х_2i, а вычитание - нижний уровень фактора х_1i.

Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по кодированным осям и начало отсчета выбирают так, чтобы верхний уровень соответствовал +1, нижний -1, а основной - 0:

где - кодированное значение фактора.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. Так как число уровней каждого фактора равно двум, то в теории планирования экспериментов рассматривается полный факторный эксперимент n². Для двух факторов план эксперимента и геометрическая интерпретация матрицы планирования 2² приведены на рис. 36.

Полный факторный эксперимент 2³ будет иметь восемь опытов, а его геометрическая интерпретация представляет собой куб.

Матрица полного факторного эксперимента строится следующим образом: в первом столбце знаки меняются поочередно, во втором - через два, в третьем - через четыре и т.д. по степени двойки. Однако полный факторный эксперимент содержит избыточную информацию для определения коэффициентов регрессии b_i, для расчета которых достаточно провести только часть полного факторного эксперимента - дробный факторный эксперимент.

Рис. 29. План и геометрическая интерпретация

эксперимента 2²

Реализуемая часть полного факторного эксперимента называется дробной репликой. Объем дробного факторного эксперимента определяется из следующих условий:

число экспериментов должно быть не меньше числа неизвестных коэффициентов в уравнении регрессии;

число экспериментов должно быть обязательно равно степени числа 2.

Так, для определения 11 коэффициентов уравнения линейной регрессии с 10 факторами требуется провести не менее 11 экспериментов. Ближайшее число по степени числа 2 - это число 16. Оно и определяет объем дробного факторного эксперимента. Так как 16 = 2⁴, а объем полного факторного эксперимента 2¹¹, то обозначение соответствующей дробной реплики 2^11-7 в силу того, что 2^11-7 = 2⁴ = 16.

Как видно из табл. 17, применение дробного факторного эксперимента для случая 15 факторов уменьшает объем расчетов по определению направления градиента в 2048 раз по сравнению с полным факторным экспериментом. Увеличение числа факторов в еще большей степени способствует повышению вычислительной эффективности этого метода.

Таблица 17

Дробные реплики

Естественно, что далеко не любые эксперименты из плана полного факторного эксперимента могут быть использованы при формировании плана дробного факторного эксперимента. Совокупность экспериментов в дробной реплике должна удовлетворять следующим свойствам:

1. Симметричность относительно центра эксперимента - алгебраическая сумма экспериментов-столбцов каждого фактора должна быть равна нулю, кроме столбца, отвечающего свободному члену b₀, т.е.

где m - номер точки опыта; i - номер фактора; М - число различных точек плана матрицы дробной реплики.

2. Нормировка сумма квадратов элементов каждого столбца равна числу точек матрицы, т.е.

3. Ортогональность - сумма построчных произведений плана матрицы любых двух столбцов равна нулю, т.е.

где j - комбинация факторов в m-й точке (i ≠ j).

Ортогональность матрицы позволяет оценить все коэффициенты регрессии независимо друг от друга, т.е. значение любого коэффициента не зависит от того, какие значения имеют другие коэффициенты.

Если план дробной реплики отвечает указанным свойствам, то математическая модель, полученная в результате эксперимента, способна предсказать значения искомого показателя у с одинаковой точностью в любых направлениях на равных расстояниях от центра эксперимента или плана матрицы (свойство рототабельности).

После обработки данных эксперимента и вычисления коэффициентов регрессия b_i определяют следующие значения основного уровня по всем факторам В основу алгоритма определения улучшенных значений основного уровня могут быть положены симплекс-метод, градиентный и др. Например, для движения по градиенту методом Бокса-Вильсона рекомендуется (рис. 29):

1) рассчитать составляющие градиента Δ_i = b_iI_i ;

2) подобрать масштаб для шага изменения основного уровня k;

3) определить новые значения основных уровней по формуле

x¹_0i = x_0i + kΔ_i

4) рассчитать значения целевой функции для точки с координатами х¹₀₁, х²₀₂, …, х¹_0n и сравнить его с наилучшим значением из предыдущей серии экспериментов;

5) если шаг выбран удачно, т.е. получено улучшение, продолжать увеличивать значения основных уровней факторов на величину kΔ_i; если произошло ухудшение, то следует уменьшить масштаб;

6) значение точки, в которой достигнуто максимальное улучшение значения целевой функции, принять за центр новой подобласти проведения эксперимента относительно этой точки вновь повторить вышеописанную процедуру и искать направление градиента.

Если значения коэффициентов регрессии b_i близки к нулю, то это означает, что недалеко находится область оптимума. Для отыскания оптимального решения в этом случае необходимо переходить на полиномиальные уравнения более высокого порядка, например использовать неполный полином второй степени.

Регрессия называется парной, если она описывает зависимость между функцией и одной переменной и имеет вид

(5)

Регрессия называется множественной, если она описывает зависимость функции от нескольких переменных и имеет вид

(6)

Если зависимости (5) и (6) являются линейными, то регрессия называется линейной, в противном случае регрессию называют нелинейной. Зависимости между параметрами объектов проектирования, как правило, являются нелинейными. Очень важной характеристикой регрессионных зависимостей является мера их достоверности, которая оценивается величиной R², находящейся в пределах

При R² = 0 величины, для которых определяются уравнения регрессии, являются независимыми; при R² = 1 имеет место функциональная (а не статистическая) зависимость. Принято считать допустимым R² = 0,7.

Чем больше статистических данных, используемых при определении уравнения регрессии, тем точнее будет определена искомая зависимость. Но при этом следует иметь в виду, что количество статистических данных не может обеспечить получение достоверной зависимости, если в действительности такой зависимости между исследуемыми величинами нет. Вместе с тем, есть минимальное количество К необходимых исходных данных, определяемое методом наименьших квадратов, с помощью которого находится уравнение регрессии. К определяется по формуле

К=М+2, (7)

где М - количество неизвестных величин в искомом уравнении регрессии.

Например, для уравнения парной регрессии:

при линейной зависимости

y = b₀ + b₁x

необходимо определить 2 величины: b₀ и b₁;

при уравнении регрессии в виде полинома 2-й степени

y = b₀ + b₁x + b₂x²

необходимо определить 3 величины: b₀, b₁, b₂.

Уравнение множественной регрессии при решении практических задач принимается, как правило, в виде полинома 2-й степени, для которого число определяемых величин находится по зависимости

M = (n + 2)(n + 1)/2 (8)

где n - число искомых переменных в (6).

Объединяя (7) и (8), нетрудно выяснить минимально необходимое количество исходных данных для определения уравнения регрессии:

K = (n + 2)(n + 1)/2 + 2. (9)

Подчеркнем, что эта величина К является нижней границей количества исходных данных, необходимых для метода наименьших квадратов. А достоверность полученного результата следует оценивать с помощью уже упомянутой величины R².

Если исходных данных, необходимых для определения уравнения регрессии нет, то их можно получить в результате проведения эксперимента. При этом прежде, чем его проводить, необходимо составить план его проведения, включающий два вопроса:

1) какие значения следует назначать переменным в эксперименте;

2) в каком сочетании различным переменным должны назначаться принятые значения.

Определяя значения переменных, задаваемых при проведении эксперимента, удобно от их абсолютных значений х_j перейти к относительным γ_j. Этот переход производится следующим образом:

γ_j = (x_j-x_j^ср)/Δx_j (10)

x_j^ср = (a_j+b_j)/2 (11)

Δx_j^ср = (b_j – a_j)/2 (12)

где а_j, b_j - задаваемые граничные условия в задаче оптимизации:

Если в (9) подставить х_j = а_j, то получим значение относительной переменной j на нижней границе

Аналогично получим на верхней границе

Среднее значение

Обратный переход от относительных значений к абсолютным, как это следует из (9), производится по зависимости

С точки зрения числа различных значений, которые назначают переменным в эксперименте, эксперименты бывают двух видов: двухуровневые; трехуровневые.

В двухуровневом эксперименте переменным придаются значения . В результате такого эксперимента может быть определено уравнение только линейной регрессии, которая, как правило, не отражает фактические зависимости и поэтому имеет низкое значение оценки достоверности R². для получения достоверных уравнений регрессии следует проводить трехуровневые эксперименты, в которых переменным назначаются три значения:

Рассмотрим, в каком сочетании следует придавать установленные значения различным переменным: начнем с двух переменных. Возможные сочетания значений переменных, называют планом эксперимента, который для двухуровневого эксперимента приведен слева на рис. 30, план трехуровневого эксперимента – справа на рис. 30.

Рис. 30. Двухуровневый и трёхуровневый эксперименты

Из этих планов видно, что число проводимых экспериментов может быть определено по зависимости

где S - число уровней, n - число переменных.

Аналогичные планы эксперимента для трех переменных приведены для двухуровневого эксперимента слева на рис. 31, для трехуровневого – справа на рис. 31.

Рис. 31. Планы эксперимента для 3-х переменных

Итак, с одной стороны мы знаем минимальное количество экспериментов, необходимое для определения коэффициентов в уравнении регрессии, с другой стороны - нам известно, как планировать двух- и трехуровневые эксперименты. Сравним эти величины.

В табл. 18 приведены следующие значения:

n - число переменных, М - число коэффициентов, которые надо определить в уравнении нелинейной регрессии, в виде полинома 2-й степени:

К - минимальное количество экспериментов, необходимое для вычисления коэффициентов в уравнении регрессии

К = М + 2,

2ⁿ - количество экспериментов в двухуровневом плане,

3ⁿ - количество экспериментов в трехуровневом плане.

Таблица 18

Количество экспериментов

Из таблицы видно, что минимально потребное число экспериментов К находится в пределах

2ⁿ < K < 3ⁿ,

следовательно, для рассматриваемого вида уравнения регрессии двухуровневых экспериментов недостаточно, а трехуровневые в полном объеме являются излишними. Сравнение этих величин приведено в двух последних столбцах таблицы:

N_недост = K – 2ⁿ

N_изл = 3ⁿ – K.

Таким образом, проведение трехуровневого эксперимента обеспечит получение исходных данных, достаточных для определения коэффициентов регрессии, но существует план эксперимента, который называется композиционным, - он позволяет обойтись без проведения излишних экспериментов. Известен целый ряд подходов к их составлению, например:

1. Принять за основу план двухуровневого эксперимента.

2. Определить недостающее число экспериментов.

N_недост = K – 2ⁿ.

3. Вычисленное число недостающих экспериментов N_недост провести при среднем значении γ = 0. В качестве примера в табл. 19 приведен композиционный план такого эксперимента для n = 3.

Таблица 19

План эксперимента

В этом плане первые 8 экспериментов представляют собой двухуровневый план, а дополнительные 4 эксперимента проводятся при средних значениях = 0. В результате проведения эксперимента по такому плану будет получено количество исходных данных, необходимых для определения уравнения регрессии в виде полинома 2-й степени. Аналогично могут быть составлены композиционные планы для любого числа переменных n. Последовательность работ для получения необходимого количества исходных данных.

1. Определить число переменных n в задаче оптимизации.

2. Принять вид уравнения регрессии и установить число искомых коэффициентов и необходимых исходных данных.

3. Составить план проведения эксперимента для определения значений переменных.

4. Перейти к абсолютным значениям переменных х_j по зависимостям

где x_j^ср, Δх_j определяются по (10) и (11).

Составить таблицу для проведения эксперимента.

Таблица составлена для трех переменных х₁, x₂, х₃ и двух искомых функций, определяемых в результате эксперимента у₁, у₂.

5. Провести эксперименты по принятому плану.

6. для каждого сочетания значений х_j записать результат эксперимента для значений у₁, у₂:

Полученная таблица представляет собой исходные данные, необходимые для определения уравнения регрессии. Очевидно, что приведенная методика дает возможность составить план эксперимента для любого количества переменных и определяемых функцией.

Эксперименты с ответственными решениями, как правило, всегда являются довольно дорогими и более длительными, чем хотелось бы. Поэтому с реальными вариантами решений экспериментировать приходится очень редко.

Целесообразно экспериментировать с математическими и компьютерными моделями решений. При этом используется теория планирования экспериментов, которая базируется на принципах активного воздействия на объект управления с целью обеспечения определенных преимуществ при построении и использовании модели объекта.

Целью экспериментов с моделями решений может быть выбор наилучших вариантов при заданных затратах или минимизация затрат для выбора вариантов с заданными значениями характеристик.

Моделью для постановки и проведения экспериментов с решениями является рассмотренная выше схематическая модель объекта с управляемыми входными характеристики - Х и выходными характеристиками - Y на фоне ошибки :

Предполагается, что ошибки  являются случайными величинами в общем случае с неизвестным законом распределения. Если ошибки являются не случайными, а систематическими, например вызванные инструментом измерения, то такие ошибки превращаются в случайные искусственно путем специальных приемов перемешивания - рандомизации их.

Рассмотрим пример моделирования получения прибыли. Предположим, что имеется следующая ситуация. Нас интересует зависимость Y - прибыли небольшой туристической фирмы от двух факторов:

Х₁ - количества сотрудников в агентстве и Х₂ - уровня цен на туристские услуги.

Положим, что количество сотрудников меняется от 3 до 6 человек, уровень цен колеблется от 90% до 110% от средних цен, а диапазон изменения прибыли колеблется от 50% до 100% по отношению к затратам.

Планирование эксперимента предполагает активное воздействие на исходные данные для создания рациональных условий построения модели объекта и удобства использования ее на практике. Полагаем, что руководитель туристического агентства может менять характеристики объекта: количество сотрудников и средний уровень цен на предоставляемые услуги. Поэтому этот эксперимент можно организовать по активной схеме полного факторного эксперимента на двух уровнях. Для этого перейдем следующим образом от натуральных характеристик Х₁ и Х₂ к безразмерным характеристикам х₁ и х₂:

Этот переход осуществляется по соотношению:

х_i = (Х_i – Х_i0)/ΔХ_i,

где ΔХ интервал варьирования i характеристики. В нашем примере этот интервал, как видно из схемы, равен 1 сотруднику. За ноль на безразмерной оси взято значение на натуральной оси

Х_i0 = 4.

для второй характеристики имеем:

Здесь за ноль взят 100% уровень цен, а за интервал варьирования 10%. Теория планирования эксперимента говорит, что в новых осях х₁ и х₂ можно построить следующую модель объекта:

Y = f(х₁,х₂) = b₀ + b₁х₁ + b₂х₂ + b₁₂х₁х₂.

Коэффициенты модели b в данном случае определятся по следующей схеме активного воздействия на объект:

u	X0	X1/x1	X2/x2	X1X2
1	+	- / 3	- / 90	+
2	+	+ / 5	- / 90	-
3	+	- / 3	+ / 110	-
4	+	+ / 5	+ / 110	+

Таблица содержит столько столбцов, сколько надо определить коэффициентов в модели. Плюсы в таблице соответствуют 1, а минусы соответствуют -1 для безразмерных характеристик искомой модели. В знаменателе стоят соответствующие значения натуральных характеристик. Таблица состоит из столбцов, Х₁ и Х₂ составляющих план эксперимента, и столбцов, которые являются вспомогательными для расчетов соответствующих коэффициентов модели - Х₀ и Х₁Х₂.

Коэффициенты b_i определяются по соотношению:

b_i =1/4 _uх_iuу_u.

В соотношение входят усредненные результаты опытов - наблюдений над объектом:

у_u = 1/n (у₁ +у₂+…+у_n)

Предположим, что наши наблюдения над объектом туристическим агентством – по спланированной таким образом схеме дали следующие результаты: Y₁ и Y₂ :

Полученные данные позволяют рассчитать коэффициенты модели:

b₀ = 1/4 (105+92+120+110) = 106,75

b₁ = 1/4 (-105+92-120+110) = -5,75

b₂ = 1/4 (-105-92+120+110) = 8,25

b₁₂ = 1/4 (+105-92-120+110) = 0,75

Модель зависимости прибыли от числа сотрудников туристического агентства и уровня цен на услуги имеет вид:

Y = 106,75 – 5,75х₁ + 8,25х₂ + 0,75х₁х₂.

Схема эксперимента позволяет следующим образом трактовать полученную модель.

Для нулевых значений характеристик, то есть для числа сотрудников 4 и 100% уровня цен на услуги прибыль равна 106,75%.

При 3 сотрудниках и 90% уровне цен, то есть при х₁ =-1 и х₂= -1 прибыль равна Y = 106,75+5,75-8,25+0,75 = 105.

При 5 сотрудниках и 90% уровне цен (х₁ = 1, х₂ = -1) прибыль равна

У= 106,75-5,75-8,25-0,75=92.

При 3 сотрудниках и 110% уровне цен (х₁ = -1, х₂=1) прибыль равна

У = 106,75 + 5,75х₁ + 8,25х₂ - 0,75х₁х₂ = 120.

Мы видим, что эксперименты с моделью объекта по определенной схеме показывают, что наилучшим вариантом решения реальной задачи по получению наибольшей прибыли будет сочетание наименьшего числа сотрудников и наибольшего уровня цен.

Полученная модель позволяет также решить и вторую задачу и сказать, что наибольшее влияние оказывает уровень цен (коэффициент b₂= 8,25), эффект числа сотрудников меньше, так как коэффициент b₁ = -5,75. Взаимодействие числа сотрудников и уровня цен характеризуется коэффициентом b₁₂= 0,75. Его величина самая маленькая, то есть эффект взаимодействия незначителен. Для подобных выводов требуется найти ошибку эксперимента и ее влияние на величину коэффициентов. Мы оставляем этот вопрос для любознательного читателя.

Полученная модель также пригодна для нахождения сочетания значений характеристик, дающего максимум прибыли. Мы рассмотрим решение этой задачи в главе Подобные эксперименты с моделями объекта вполне доступны любому ЛПР в любой организации.

Активный эксперимент предоставляют ЛПР определенные преимущества перед обычной схемой эксперимента и его коротко можно сформулировать следующим образом:

• простой способ построения модели,

• незначительные затраты на проведение эксперимента,

• наглядная интерпретация результатов эксперимента по построенной модели,

• возможность выделения наиболее значимых характеристик,

• возможность определения оптимальных значений характеристик.