2.4.3. Пример реализации конечного автомата с помощью сфэз

Пусть задана таблица состояний конечного автомата.

Таблица 14

Текущее состояние	Следующее состояние		Выход
	0	1	0	1
s0	s0	s1	1	0
s1	s2	s1	0	1
s2	s0	s1	1	1

Требуется реализовать данный автомат с помощью СФЭЗ.

Анализ таблицы состояний показывает, что алфавиты . Это говорит о том, что символы входного и выходного алфавитов можно не кодировать. Для решения поставленной задачи кодируем только внутренние состояния конечного автомата посредством двух булевых переменных и 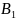. Пусть состояния кодируются следующим образом:

Таблица 15

s0	0	0
s1	1	0
s2	0	1

В результате получаем следующую систему частично определённых булевых функций

Таблица 16

A				B
0	0	0		1	0	0
0	1	o		0	0	1
0	0	1		1	0	0
1	0	0		0	1	0
1	1	0		1	1	0
1	0	1		1	1	0
0	1	1		-	-	-
1	1	1		-	-	-

Здесь булевы переменные и отображают код следующего состояния автомата.

Логические функции , и можно физически реализовать посредством следующих логических схем.

,

,

.

После проведения минимизации системы частично определённых булевых функций, будем иметь:

,

,

.

Объединяя три последние логические схемы, получим модель конечного автомата в виде СФЭЗ.

Рис. 8

Здесь изображены триггеры (ТР) – устройства, технически реализующие единичную задержку. При этом, переменные и отражают те состояния триггеров, в которых они должны находиться в следующий момент времени.

Таким образом, получаем СФЭЗ, реализующую таблицу состояний заданного конечного автомата.

2.4.4. Эксперименты с автоматами

Эксперимент с автоматами — это способ получений информации о внутренней структуре автоматов по их поведению. Основная задача экспериментов — получить сведения о строении автомата путем наблюдения его реакции на внешние воздействия.

Рассмотрим автоматы, в которых не выделены начальные состояния. В этом случае автомат задается пятеркой (A,S,B,φ, ). Множество всех конечных слов в алфавите обозначается . Пусть автомат (A,S,B,φ, ) находится в состоянии и на вход подаётся слово . Тогда на выходе будет некоторое слово и после подачи всего слова автомат оказывается в состоянии . Раcширяя функции и , положим .

Определение 1. Два состояния и автомата (A,S,B,φ, ) называются отличимыми, если существует входное слово такое, что . При этом слово называется экспериментом, отличающим от . Длину слова I( ) называют длиной эксперимента.

Теорема 3 (Мура). Если в автомате состояния и отличимы и , то существует эксперимент , отличающий и , длина которого .

Определение 2. Пусть даны два автомата и , т.е. автоматы, имеющие одинаковые входной и выходной алфавиты. Пусть и . Говорят, что эксперимент отличает состояния и , если .

Теорема 4. Даны два автомата и , причем и . Тогда, если состояния и отличимы, то существует отличающий их эксперимент , длина которого .