1.8. Энтропия источника без памяти как скорость создания информации

Факт существования высоковероятных множеств дискретного ис­точника без памяти играет фундаментальную роль в формулировании и доказательствах прямых теорем кодирования теории информации. В случае эффективного кодирования источника это представляется осо­бенно наглядным. Прямая теорема кодирования источника без памя­ти является следствием теоремы о высоковероятных множествах та­кого источника.

Предполагается, что источник без памяти выбирает сообщения из ансамбля и H(A) есть энтропия этого ансамбля, так что пря­мая теорема кодирования источника может быть сформулирована сле­дующим образом:

Пусть R> Н(А), тогда для любого положительного р_е найдется код со скоростью R, который кодирует дискретный источник без памяти с вероятностью ошибки, не превышающей р_е.

Предполагая, что существует код со скоростьюR, кодирующий ис­точник с вероятностью ошибки р_е, имеют ввиду, что можно найти такое п, код с М = 2^nR кодовыми словами и множество однозначно коди­руемых последовательностей , для которых вероятность ошибки не превосходит р_е. В соответствии с теоремой о высоковеро­ятных множествах источника без памяти для любых положительных и существует такоеN, что для любогоn> N вероятность появления на выходе источника последовательности , не принадлежащей высокове­роятному множеству , не превосходит . Поэтому, если выбрать в качестве множества однозначно кодируемых последовательностей под­множество , то вероятность ошибки декодирования не будет пре­восходить = р_е. Вместе с тем, количество кодовых слов оказывается равным числу элементов

Таким образом, скорость создания информации оказывается рав­ной энтропии источника без памяти; при этом в среднем на каждое со­общение источника будет приходиться кодовых символов.

Более строгое обоснование указанного толкования энтропии связано с формулировкой обратной теоремы:

Для любого R< Н найдется зависящее от R положительное число такое, что для всех n и для всех равномерных кодов со скоростью R вероятность ошибочного декодирования больше .

(Дается без доказательства)

1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале

Избыточность определяют так же, как и для источника дискретных сигналов:

(1.20)

Избыточность источника равна нулю только в случае, когда распределение сигнала является гауссовским.

При определении эпсилон-характеристик источников непрерывных сигналов критерием близости служило среднеквадратичное отклонение одного сигнала от другого. Если выбрать другую меру близости сигналов – другую метрику пространства сигналов, можно получить другие эпсилон-характеристики источников. Наибольшее распространение получил среднеквадратический критерий близости сигналов.

Количество информации, содержащееся в одной непрерывной случайной величине относительно другой, определим как разность безусловной и условной дифференциальных энтропий:

(1.21)

1.10. Скорость передачи информации и пропускная способность в непрерывном канале

Непрерывным каналом называется канал, предназначенный для передачи непрерывных сообщений. Канал считается заданным, если известны статистические данные о сообщениях на его входе и выходе и ограничения, накладываемые на входные сообщения физическими характеристиками канала.

При рассмотрении информационных характеристик канала: (скорости передачи, пропускной способности, коэффициента использования) применяют модель реального канала, называемую гауссовым каналом, предполагая, что по каналу передаются сигналы с постоянной средней мощностью, статистические связи между сигналами и помехой отсутствуют (аддитивная помеха), ширина спектра сигнала и помехи ограничены полосой пропускания канала, а в канале действует флуктуационная помеха ограниченной мощности с равномерным частотным спектром и нормальным распределением амплитуд ("белый шум").

Если X(t) рассматривать как переданный сигнал, Y(t) – как принятый, а E(t) – как аддитивную помеху в непрерывном канале, то скорость передачи информации по непрерывному каналу (среднее количество информации, которое можно передать по каналу в единицу времени) равна

(1.22)

где

(1.23)

(1.24)

(1.25)

(1.26)

Скорость передачи в предположении, что передаваемые сообщения имеют структуру "белого шума", составит

(1.27)

где – отношение средних мощностей сигнала и помехи на выходе приёмника; – полоса частот передаваемого сообщения.

Пропускная способность (максимальное значение скорости передачи информации по каналу) непрерывного сигнала:

(1.28)

Для гауссова непрерывного канала с дискретным временем

(1.29)

Учитывая, что

(1.30)

(1.31)

тогда

(1.32)

Если в канале нет искажений и помех, то 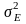можно рассматривать как мощность шумов квантования при дискретной передаче непрерывных сигналов. В канале с помехами мощность шумов квантования складывается с мощностью помех, следовательно, в этом случае необходимо рассматривать как суммарную мощность помехи и шума квантования. Мощность шума квантования при равномерном квантовании:

(1.33)

где - шаг квантования.

Для непрерывного канала с непрерывным временем и формула переходит в известную формулу Шеннона для пропускной способности гауссова непрерывного канала с флуктуационной помехой:

(1.34)

где – полоса пропускания канала; - отношение средних мощностей сигнала и помехи на входе приёмника.

Из (1.34) следует, что одну и ту же пропускную способность можно получить при различных соотношениях и . Кроме того, выражение (1.34) указывает теоретический предел скорости передачи информации по каналу связи при ограниченной средней мощности передаваемых сигналов и при наличии аддитивной помехи в виде "белого шума" с ограниченным спектром.

Так как энергетический спектр помехи типа "белого шума" равномерен в пределах от 0 до , мощность можно выразить через удельную мощность на единицу частоты. Тогда выражение (1.34) примет вид

(1.35)

При расширении полосы пропускания канала пропускная способность увеличивается, но стремиться к конечному пределу:

(1.36)

Это ограничение, вносимое помехой с уровнем мощности , которое не может быть превышено без увеличения мощности сигнала.

Если плотность распределения w(x) непрерывных сообщений, вырабатываемых источником информации, отличается от гауссовской, то скорость передачи информации будет меньше.

Необходимо отметить существенную разницу Rt и С. Пропускная способность С характеризует канал, его предельные возможности независимо от системы источник-потребитель, а скорость передачи Rt характеризует некоторую конкретную систему передачи информации.

Кроме того, как следует из (1.37), если сигнал смешан с шумом, то амплитуда сигнала может быть измерена лишь с точностью до эффективного значения шума. Другими словами, неопределенность оценки точного значения амплитуды сигнала равна квадратному корню из среднего квадрата шумового напряжения. Как следует из указанных выше предположений, изменение входного сигнала меньше, чем , приемник не различает. Следовательно, число уровней, которое может быть различимо без ошибок, определится из выражения

(1.37)

Следовательно

(1.38)

Таким образом получено наибольшее количество информации, переносимое каждым импульсом, имеющим М различных уровней