
- •Введение
- •1. Энтропия источников сообщений
- •1.1. Дискретные ансамбли и источники
- •1.2. Количество информации в дискретном сообщении. Энтропия ансамбля
- •1.3. Условная информация. Условная энтропия. Совместная энтропия дискретного источника
- •1.4. Энтропия дискретного стационарного источника на сообщение
- •1.5. Избыточность источника дискретных сообщений
- •1.6. Эффективное кодирование. Кодирование источника равномерными кодами
- •1.7. Высоковероятные множества постоянного дискретного источника
- •1.8. Энтропия источника без памяти как скорость создания информации
- •1.9. Избыточность источника непрерывных сигналов. Количество информации в непрерывном канале
- •1.10. Скорость передачи информации и пропускная способность в непрерывном канале
- •2. Кодирование информации
- •2.1. Неравномерное кодирование с однозначным декодированием
- •2.2. Оптимальные неравномерные двоичные коды
- •2.3. Кодирование для исправления ошибок: Основные положения
- •2.4. Постановка задачи кодирования
- •2.5. Прямая теорема о кодировании в канале с шумами
- •2.6. Обратная теорема кодирования
- •2.7. Основная теорема Шеннона, ограничение возможностей использования оптимального кодирования на практике
- •3. Коды, исправляющие ошибки
- •3.1. Блоковые и сверточные коды
- •3.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность
- •3.3. Линейные блоковые коды
- •3.4. Порождающая и проверочная матрицы. Кодирование с помощью матриц g и н
- •3.5. Декодирование по стандартной таблице
- •3.6. Циклические коды
- •3.7. Кодирующие устройства циклических кодов
- •3.8. Декодирование циклических кодов по синдрому
- •3.9. Мажоритарное декодирование
- •4. Энтропия в контексте защиты информации от помех при передаче по каналу связи
- •4.1. Меры искажения. Постановка задачи защиты информации от помех при передаче по каналу связи
- •4.2. Свойства функции скорость-искажение
- •4.3. Простые примеры вычисления функции скорость-искажение
- •4.4. Функция скорость-искажение для гауссовских последовательностей
- •4.5. Эпсилон-производительность источника
- •4.6. Дифференциальная энтропия
- •4.7. Свойства дифференциальной энтропии
- •4.8. Эпсилон - энтропия источника сообщений
- •4.9. Обратная теорема кодирования для дискретного постоянного источника при заданном критерии качества
- •4.10. Прямая теорема кодирования с заданным критерием качества
- •4.11. Аксиоматическое введение в теорию энтропии вероятностных схем
- •4.12. Энтропия и условная энтропия объединенной вероятностной схемы и их свойства
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
2.3. Кодирование для исправления ошибок: Основные положения
Все коды, исправляющие ошибки, основаны на одной общей идее: для исправления ошибок, которые могут возникнуть в процессе передачи или хранения информации, к ней добавляется некоторая избыточность. По основной схеме (используемой на практике), избыточные символы дописываются вслед за информационными, образуя кодовую последовательность или кодовое слово {codeword). В качестве иллюстрации на рис. 2.4 показано кодовое слово, сформированное процедурой кодирования блокового кода (blockcode).Такое кодирование называют систематическим (systematic). Это означает, что информационные символы всегда появляются на первых к позициях кодового слова. Символы на оставшихся п-к позициях являются различными функциями от информационных символов, обеспечивая тем самым избыточность, необходимую для обнаружения или исправления ошибок. Множество всех кодовых последовательностей называют кодом, исправляющим ошибки (errorcorrectingcode),и обозначают через С.
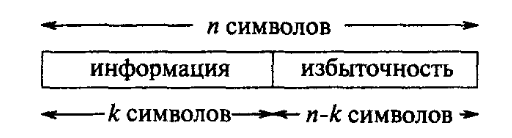
Рис. 2.4. Систематическое блоковое кодирование для исправления ошибок
2.4. Постановка задачи кодирования
Назначение кодера и декодера канала заключается в обеспечении надежной связи между источником и получателем сообщений и максимально возможном уменьшении влияния шумов. Следует упомянуть о некоторых принципиальных возможностях обеспечения высокий надежности передачи. Одна из них связана с передачей в двоичном симметричном канале, в котором параметр р — вероятность ошибки не превосходит 0,5, двух возможных сообщений — 0 и 1 — с многократным повторением каждого и принятием решений по мажоритарному правилу: 0 (1), если в переданной последовательности из n нулей (единиц) более половины оказываются нулями (единицами). В пределе при неограниченном возрастании n вероятность ошибочного декодирования стремится к нулю в силу справедливости закона больших чисел. Однако скорость передачи информации при таком методе кодирования также стремится к нулю, и практической ценности такой метод не представляет.
Другую возможность безошибочной передачи в канале с шумами конечной интенсивности связывают с созданием системы из n многопозиционных ортогональных сигналов, обеспечивающих в асимптотике при неограниченном возрастании n и определенном соотношении интенсивностей сигналов и шума безошибочное различение сигналов на выходе канала . Бесперспективность использования такого способа абсолютно надежной передачи сообщений вытекает, в частности, из необходимости использования в системе передачи неограниченной полосы частот электромагнитных колебаний.
В теории информации показано, что произвольно малая вероятность ошибки может быть достигнута и при конечных скоростях передачи сигналов, занимающих конечную полосу частот, за счет усложнения методов кодирования и соответственно декодирования.
Рассмотрим
задачу кодирования источника дискретных
сообщений А,
имеющего энтропию
Н(А).
Пусть
В
— множество кодовых блоков, из числа
которых выбираются слова, предназначенные
для передачи сообщений по каналу связи
с помехами;
Н(В)
— энтропия дискретного ансамбля
В.
Обозначим через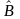 и
и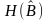 — ансамбль кодовых слов, появляющихся
на выходе канала, и его энтропию. Поскольку
при передаче сигналов по каналу с
помехами существует не нулевая вероятность
перехода какой-то части кодовых символов
в ложные (с вероятностью р),
имеют место следующие неравенства,
характеризующие взаимную информацию
между этими ансамблями:
— ансамбль кодовых слов, появляющихся
на выходе канала, и его энтропию. Поскольку
при передаче сигналов по каналу с
помехами существует не нулевая вероятность
перехода какой-то части кодовых символов
в ложные (с вероятностью р),
имеют место следующие неравенства,
характеризующие взаимную информацию
между этими ансамблями:
 (2.1)
(2.1)
Поставим идеализированную на первый взгляд задачу кодирования в канале с помехами, обеспечивающего безошибочную передачу сообщений с конечной скоростью. Для решения поставленной задачи необходимо обеспечить абсолютную надежность канала и, следовательно, выполнение равенств
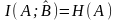 (2.2)
(2.2)
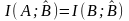 (2.3)
(2.3)
Неравенство (2.5) свидетельствует о том, что для решения поставленной задачи в ансамбль кодовых блоков на входе канала необходимо вводить избыточность, т.е. количество кодовых слов на входе канала должно превышать число состояний кодируемого источника, так что в используемом коде количество кодовых символов п в слове может иметь произвольное значение. При этом целесообразно ввести следующее определение кода и скорости кода для канала с помехами.
Кодом длиной n и объемом М для канала называется множество из М пар ,
 ,где
,где
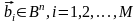 -
последовательности длины n,
образованные входными сигналами
канала и называемые кодовыми словами
(
-
последовательности длины n,
образованные входными сигналами
канала и называемые кодовыми словами
(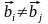 при i
≠ j)
и
при i
≠ j)
и
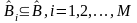 ,
i
= 1,2,
...,М, — решающие области, образованные
выходными последовательностями канала,
причем при i
≠ j
множества
,
i
= 1,2,
...,М, — решающие области, образованные
выходными последовательностями канала,
причем при i
≠ j
множества
 и
и
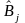 не пересекаются.
не пересекаются.
Если
задан код, то тем самым задано как
множество кодовых слов, так и правило,
по которому приемник принимает решение
о переданном кодовом слове: если на
входе канала появляется последовательность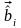 и
и
 ,
то приемник принимает решение, что
передавалось слово
,
то приемник принимает решение, что
передавалось слово
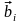 .
.
Скоростью кода называется величина
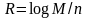 , (2.6)
, (2.6)
43
Если бы кодовые слова имели бы одинаковые вероятности появления (например, относились бы к асимптотически равновероятным типичным последовательностям, появляющимся на выходе кодера источника), то величина logM представляла бы максимальное количество информации, которое передавалось бы одним кодовым словом и, следовательно, скорость кода представляла бы максимальное количество информации, передаваемое с помощью одного кодового символа. Скорость кода измеряется в битах на символ. Число кодовых блоков не может превышать общего числа последовательностей длины п, образованных символами входного алфавита канала. Отсюда следует, что R ≤ logm, где т — мощность алфавита. В двоичном каналеR ≤ 1. Очевидно, что двоичный код длины n, имеющий скоростьR, имеет объем М = 2nR.
При передаче сообщений по каналу с помехами возможны ошибки декодирования. Обозначим через р,- вероятность ошибочного декодирования словаbi, не оказавшегося в решающей области Вi.
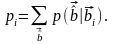
В
качестве меры надежности передачи
кодовых слов могут быть использованы
либо максимальная вероятность ошибки
рmах
= mах{р1,
...,рM}.
либо средняя вероятность ошибки
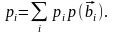
Далее сформулируем теоремы Шеннона о кодировании в канале с шумами.
Пусть С — пропускная способность дискретного канала без памяти. При любом R< С и любом положительном 6 существует код достаточно большой длины n, максимальная вероятность ошибки которого удовлетворяет неравенствуpmax ≤ δ. (Прямая теорема кодирования).
Для всякого R> С найдется положительное число 6 такое, что Pmin ≥ δ для любого n и любого кода. (Обратная теорема кодирования).
