4.4. Функция скорость-искажение для гауссовских последовательностей

В предыдущем параграфе по сути дела вычислялась функция скорость- искажение для случайных величин, а теперь мы должны сначала рас­смотреть случайные векторы, а затем и случайные процессы. При вычислении дифференциальной энтропии произвольного вектора мы воспользовались тем, что: а) при линейном преобразовании гауссовского вектора изменение его диффе­ренциальной энтропии зависит от определителя матрицы преобразова­ния; б) из случайного вектора с заданной корреляционной матрицей с помощью линейного преобразования можно получить вектор с незави­симыми компонентами; в) гауссовский вектор имеет наибольшую диф­ференциальную энтропию среди векторов с заданной корреляционной матрицей. Эти знания будут использованы ниже при вычислении функ­ции скорость-искажение.

В данном параграфе рассматривается только квадратическая мера качества, и в качестве первого шага подсчитаем функцию скорость-искажение для последовательности независимых (но не обязательно оди­наково распределенных) гауссовских с.в. с совместной плотностью

),

где

Нам предстоит минимизировать взаимную информацию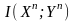 при условии, что среднеквадратическая ошибка на один символ не превышает заданной величины D. Получаем

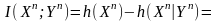
(4.31)

Введем обозначение для ошибки вi-й компоненте вектора х.

(4.5)

Понятно, что неравенства можно обратить в равен­ства соответствующим выбором условного распределения .

Нужно теперь отыскать минимум правой части (4.5) по всем неот­рицательным таким, что

(4-33)

Заметим теперь, что введение дополнительного ограничения

(4.34)

не приводит к потере минимума. Действительно, предположим, что ми­нимум достигнут при таком наборе что при некоторомi имеем и при некоторомj имеет место .Очевидно, замена на и сохраняет ошибку неизменной, уменьшая слагаемое с номеромj в правой части. Следовательно, выбор неоптимален.

Заметим теперь, что правая часть (4.5) выпукла как функция ар­гументов поскольку она является суммой выпуклых функ­ций. Поэтому любое выравнивание значений (не нарушающее ограничений) приводит к уменьшению суммы. Отсюда следует, что минимум суммы будет достигаться в том случае, когда все одинаковы. При этом они должны быть равны некоторому такому, чтобы выполнялось. Окончательный результат сформулируем .в в ix де с л е дующей теоремы.

Теорема. Для гауссовского вектора с независимыми компонента­ми, имеющими дисперсии 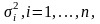при квадратической мере ис­кажения функция скорость-искажение вычисляется по формуле

(4.35)

Где выбираем таким, что

(4.6)

Полученные соотношения заслуживают дополнительного обсужде­ния. Прежде всего, заметим, что как средняя ошибка для вектора, так и средняя ошибка для отдельных компонент будет не больше . Это означает, что при заданных требованиях к средней ошибке D все компоненты, дисперсия которых меньше D, игнорируются, и при кодировании нужно принимать во внимание только компоненты с большой дисперсией. Это правило подсчета затрат на кодирование получил название "обратного принципа заполнения водой". Объяснение такого названия будет дано ниже после того, как полученные результаты будут обобщены на гауссовские случайные процессы.

Рассмотрим теперь гауссовский векторx = (x₁,x₂, ...,x_n) с произ­вольной корреляционной матрицейK_n. Напомним, что с помощью ортогонального преобразования (умножения на матрицу из собственных векторов) из х можно получить вектор с независимыми компонентами с дисперсиями, равными собственным числам матрицы K_n

Напомним, что при взаимно однозначном преобразовании ансамблей средняя взаимная информация не изменяется. Кро­ме того, ортонормированное преобразование векторов сохраняет рассто­яние между векторами. С помощью этих аргументов легко приходим к следующему утверждению.

Теорема. Для n-мерного гауссовского вектора с корреляционной матрицей K_n, при квадратической мере искажения функция скорость- искажение вычисляется по формуле

(4.7)

где - собственные числа K_n, а выбирается таким, что

(4.8)

Перейдем теперь к наиболее важному случаю, когда наблюдаемая на выходе источника последовательностьx₁,x₂,... - стационарная гауссовская с корреляционной функцией . Спектральная плотность мощности

и сформулирована теорема, связывающая дифференциальную энтро­пию процесса с его спектральной плотностью мощности.

Повторим, что если разбить область значений на достаточно ма­лые интервалы, то интегралы от по этим интервалам характеризу­ют энергию процесса в соответствующих спектральных диапазонах. При этом в силу свойств преобразования Фурье случайные значения сигналов в этих диапазонах асимптотически (с увеличением n) некоррелированы. Для гауссовских процессов некоррелированность эквивалентна независимости. Поэтому к сигналам в частотных поддиапазонах можно применить теорему. Эти рассуждения могут служить эвристическим обоснованием следующей теоремы.

Теорема. Для стационарного гауссовского процесса с ограничен­ной и интегрируемой спектральной плотностью мощности , при квадраггшческой мере искажения функция скорость-искажение вычис­ляется по формуле

(4.9)

где выбирается таким, что

(4.10)

Рис. 4.5. Функция скорость-искажение для гауссовского источника

Интерпретация вычислений показана на рис. 4.5. Представьте себе, что на гладкую поверхность воды опускается крышка неправильной формы. Благодаря принципу сообщающихся сосудов уро­вень воды поддерживается постоянным, в нашем случае этот уровень, в нашем случае этот уровень определяется значением параметра .Эту графическую интерпритацию называют "принципом заполнения водой".

При вычислении интегрирование выполняется в тех интервалах частот , где спектральная плотность превышает уровень .