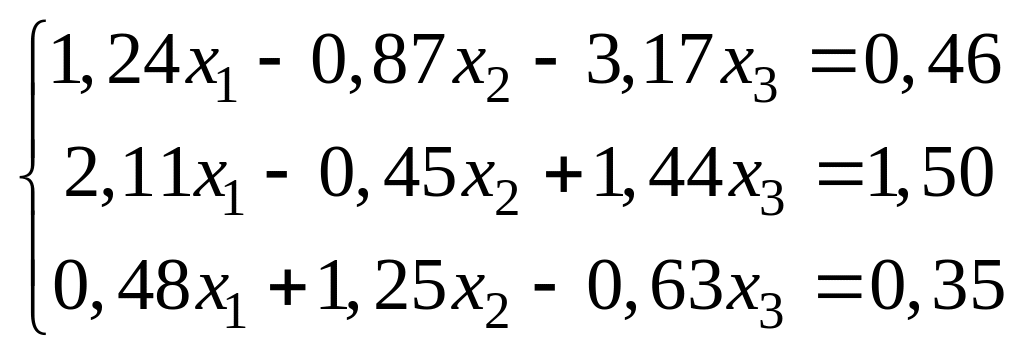- •Часть 1
- •Часть 1
- •Лабораторная работа № 1 табулирование функции на интервале. Построение графика функции
- •Варианты исходных данных
- •Алгоритм программы
- •Контрольные вопросы
- •Содержание отчета
- •Лабораторная работа № 3 приближенноевычисление определенных интегралов
- •Контрольные вопросы
- •Лабораторная работа № 4 решение системы линейных уравнений методом гаусса с выбором главного элемента
- •Контрольные вопросы
- •Лабораторная работа № 5 аппроксимация функции по методу наименьших квадратов
- •Краткое описание метода
- •Контрольные вопросы
- •Содержание отчета
- •Содержание
- •Часть 1
- •394026 Воронеж, Московский просп.,14
Контрольные вопросы
1. В чем состоит метод левых прямоугольников?
2. В чем состоит метод центральных прямоугольников?
3. В чем состоит метод трапеции?
4. В чем состоит метод Симпсона?
5. Какой из рассмотренных методов точнее и почему?
Содержание отчета
Отчет должен содержать постановку задачи, расчетные формулы, текст программы и результаты расчетов, выведенные на экран.
Лабораторная работа № 4 решение системы линейных уравнений методом гаусса с выбором главного элемента
Задание. Решить систему линейных алгебраических уравнений методом Гаусса с точностью до 0,001, а также найти определитель матрицы этой системы.
Краткое описание метода
Методом
Гаусса называют
точный метод решения невырожденной
системы
(![]() )
линейных алгебраических уравнений,
состоящий в том, что последовательным
исключением неизвестных систему
)
линейных алгебраических уравнений,
состоящий в том, что последовательным
исключением неизвестных систему
![]() ………(4.1)
………(4.1)
приводят к эквивалентной системе с треугольной матрицей

решение которой, находят по рекуррентным формулам
![]()
Существует много вариантов этого метода.
Рассмотрим схему
с выбором главного элемента.
Предположим, что в исходной системе
(4.1) ![]() ,
и разделим обе части первого уравнения
системы на
,
и разделим обе части первого уравнения
системы на ![]() В результате получим
В результате получим
![]()
где ![]() С помощью уравнения (4.3) исключим во всех
уравнениях системы (4.1), начиная со
второго, слагаемые, содержащие
.
Для этого умножаем обе части уравнения
(4.3) последовательно на
С помощью уравнения (4.3) исключим во всех
уравнениях системы (4.1), начиная со
второго, слагаемые, содержащие
.
Для этого умножаем обе части уравнения
(4.3) последовательно на
![]() и
вычитаем
соответственно из второго, третьего,
…,
п-го уравнения
системы (4.1). В результате получаем
систему, порядок которой на единицу
меньше порядка исходной системы:
и
вычитаем
соответственно из второго, третьего,
…,
п-го уравнения
системы (4.1). В результате получаем
систему, порядок которой на единицу
меньше порядка исходной системы:
 ,
где
,
где ![]()
В результате n-кратного
повторения этого преобразования получим
систему (4.2) с треугольной матрицей,
которая эквивалентна системе (4.1) и легко
решается следующим образом. Из последнего
уравнения находим ![]() ,
подставляя
в предпоследнее уравнение, найдем
,
подставляя
в предпоследнее уравнение, найдем ![]() ,
затем
,
затем ![]() и т.д. до
.
находим из первого уравнения системы.
Таким образом, вычисления по методу
Гаусса распадаются на два этапа: на
первом этапе, называемом
прямым ходом метода Гаусса,
исходную систему преобразуют к
треугольному виду. На втором этапе,
который называют
обратным ходом, решают
треугольную систему (4.2), эквивалентную
исходной. Коэффициенты
и т.д. до
.
находим из первого уравнения системы.
Таким образом, вычисления по методу
Гаусса распадаются на два этапа: на
первом этапе, называемом
прямым ходом метода Гаусса,
исходную систему преобразуют к
треугольному виду. На втором этапе,
который называют
обратным ходом, решают
треугольную систему (4.2), эквивалентную
исходной. Коэффициенты ![]() называют
ведущими элементами метода
Гаусса. На каждом шаге предполагалось,
что
называют
ведущими элементами метода
Гаусса. На каждом шаге предполагалось,
что ![]() .
Если окажется, что это не так, то в
качестве ведущего элемента можно
использовать любой другой ненулевой
коэффициент системы. Однако, если
коэффициент
.
Если окажется, что это не так, то в
качестве ведущего элемента можно
использовать любой другой ненулевой
коэффициент системы. Однако, если
коэффициент ![]() мал, то после деления на этот элемент и
вычитания
k-го
уравнения из последующих возникают
большие погрешности округления. Чтобы
избежать этого, на каждом этапе уравнения
переставляют так, чтобы на главной
диагонали оказался наибольший по модулю
элемент
k-го
столбца. Если матрица системы хорошо
обусловлена, то в методе Гаусса с выбором
главного элемента погрешности округления
невелики. Одновременно с решением
системы можно найти определитель матрицы
системы. Нетрудно убедиться, что
определитель матрицы системы равен
произведению ведущих элементов, т.е.
мал, то после деления на этот элемент и
вычитания
k-го
уравнения из последующих возникают
большие погрешности округления. Чтобы
избежать этого, на каждом этапе уравнения
переставляют так, чтобы на главной
диагонали оказался наибольший по модулю
элемент
k-го
столбца. Если матрица системы хорошо
обусловлена, то в методе Гаусса с выбором
главного элемента погрешности округления
невелики. Одновременно с решением
системы можно найти определитель матрицы
системы. Нетрудно убедиться, что
определитель матрицы системы равен
произведению ведущих элементов, т.е.
![]() При этом необходимо учесть изменение
знака определителя при перестановке
строк.
При этом необходимо учесть изменение
знака определителя при перестановке
строк.
Варианты исходных данных
1 13 |
|
7 19 |
|
2 14 |
|
8 20 |
|
3 15 |
|
9 21 |
|
4 16 |
|
10 22 |
|
5 17 |
|
11 23 |
|
6 18 |
|
12 24 |
|
Схема алгоритма метода.

Алгоритм программы
Задание константы n;
описание переменных a, x, max_a, b, det, s, i, j, k, i_max, znak;
начало исполняемой части программы
задание значений коэффициентов системы; znak=1; det=1;
начало цикла по k от 1 до n-1 max_a=0; i_max=k;
в
цикле по i
oт
k
до n
если ![]() , то
, то
![]()
если
![]() то:
то:
начало цикла по j от k до n+1 b=a(k,j); a(k,j)=a(i_max,j); a(i_maax,j)=b
конец цикла по j;
znak=-znak;
det=det*a(k,k);
в цикле по j от n+1 до k a(k,j)=a(k,j)/a(k,k);
в цикле по i от k+1 до n в цикле по j от n+1 до k
a(i,j)=a(i,j)-a(i,k)*a(k,j)
конец цикла по k
det=det*a(n,n)*znak; вывод значения определителя;
в цикле по j от n+1 до n a(n,j)=a(n,j)/a(n,n);
x(n)=a(n,n+1)
начало цикла по i от n-1 до 1
s=0; в цикле по j от i+1 до n s=s+a(i,j)*x(j);
x(i)=a(i,n+1)-s
конец цикла по i; в цикле по i от 1 до n вывод x(i) с тремя цифрами после запятой
конец программы.