5.14. Остовные деревья

Остовным деревом (остовом или каркасом) связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом. Остовное дерево графа не единственно.

На рис. 37 изображен граф G и два его остовных дерева G₁ и G₂.

Теорема. Число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно цикломатическому числу графа

ν(G)= m – n + k,

где m – число дуг, n – число вершин, k – число компонент связности графа

Следствие 1. Граф G является лесом тогда и только тогда , когда ν(G)=0.

Следствие 2. Граф G имеет единственный цикл тогда и только тогда, когда ν(G)=1.

Следствие 3. Граф, в котором число ребер не меньше, чем число вершин, содержит цикл

Для графа рис. m=5, n=4, k =1. Следовательно, надо удалить из графа две дуги, чтобы получить остов. Остовами этого графа будут графы G₁ и G₂.

Для графа G, изображенного на рис. 38, m =8, n =7, k =2. Следовательно, надо удалить из графа три дуги, чтобы получить остов. Это можно сделать так, чтобы получился граф G₁, который представляет собой лес из двух деревьев.

Существует простой способ определить количество различных остовов мультиграфа с n вершинами. Для этого нужно записать матрицу A размера , по главной диагонали которой выписаны степени вершин, а недиагональные элементы равны взятому со знаком минус числу ребер, связывающих вершины i и j. Вычислив минор любого элемента главной диагонали матрицы A, получим искомое число возможных остовов графа. Например, для графа на рис. 39 имеем:

1

2

3

4

Рис. 39

, ,

т.е. получаем 12 различных каркасов.

Эффективным методом построения каркаса графа является “подключение” очередного ребра к каркасу без образования циклов. Процедура основана на просмотре в произвольном порядке ребер исходного графа и может быть представлена как процесс окрашивания их. В синий цвет окрашиваются ребра, включаемые в остов, а в красный –ребра, не включаемые в остов. При рассмотрении ребра осуществляется проверка того, не образует ли данное ребро в совокупности с синими ребрами, уже включенными в остов, цикл. Поскольку синие ребра, включенные в остов в процессе присоединения, составляют граф, имеющий одну или несколько компонент связности, то следующая присоединяемое ребро либо попадает в «букет» или «букеты» одной вершиной (встраивается в одну из компонент связности, участвуя в построении каркаса), либо двумя (происходит образование цикла, а ребро бракуется).

5.15 Взвешенные графы. Экстремальные остовы графов

Если требуется построить каркас наиболее экономичным образом, например, построить автомобильные дороги, связывающие дачные поселки, так, чтобы их суммарная длина была наименьшей, то задачи подобного рода решаются с помощью взвешенных графов.

Любой простой граф называется взвешенным графом, если каждому ребру приписывается вес μ_i, выражающий численно расстояние, стоимость или иную величину, характеризующую взаимосвязь между парами вершин графа.

Для описания взвешенного графа (орграфа) используется взвешенная матрица смежности размерности . Каждый элемент задает вес («стоимость») ребра (дуги). Для простых графов взвешенная матрица смежности симметрична относительно главной диагонали.

Пример 5.8. Графу, изображенному на рис. 40, соответствует взвешенная матрица смежности

.

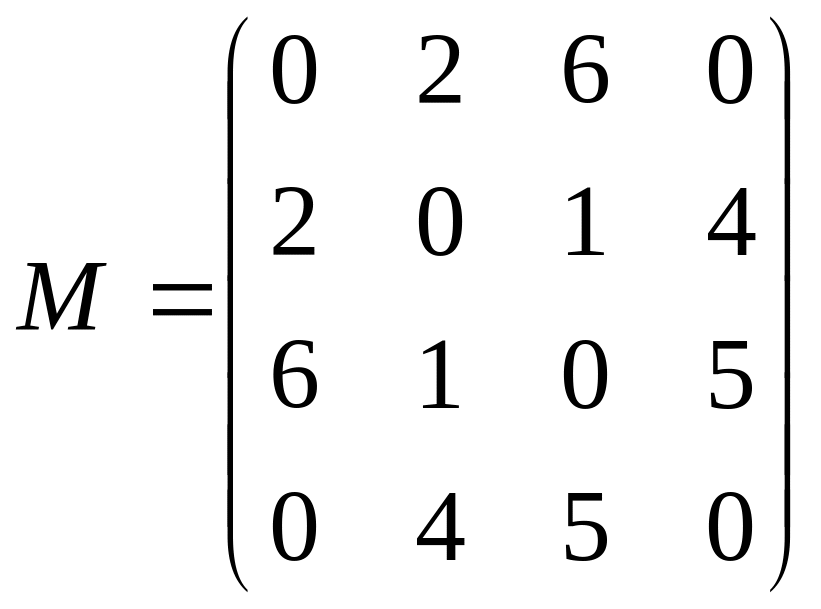Требуется выявить такой остов этого графа, чтобы суммарный вес ветвей остова был минимальным (или максимальным). Такой остов графа называют его экстремальным деревом.

Минимальным каркасным деревом графа является каркасное дерево во взвешенном графе, имеющее минимальный общий вес ребер.

Для решения задач такого рода разработаны эффективные алгоритмы, например, алгоритмом Краскала. На первом шаге выбирается первая ветвь искомого остова, для чего выбирается ребро графа с наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается минимальное по весу ребро и, если оно не образует цикла с ранее выбранными ветвями, вводится в остов. Построение заканчивается после отбора для остова n-1 ребер.

П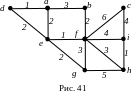 ример 5.9 Применим алгоритм Краскала для нахождения минимального каркаса графа, изображенного на рис. 41.

Упорядоченный по возрастанию стоимости список ребер выглядит так: (a,d)₁, (e,f)₁, (h,i)₁, (a,e)₂, (b,f)₂, (d,e)₂, (e,g),₂ (a,b)₃, (f,g)₃, (f,h)₄, (c,i)₄, (f,i)₄, (g,h)₅, (c,f)₆.

Действуя по алгоритму, последовательно поместим в минимальное каркасное дерево T ребра (a,d), (e,f), (h,i), (a,e) и (b,f). На следующем шаге из списка будет взято ребро (e,g),

поскольку оно в списке после ребра (b,f) оказалось первым, не приводящим к образованию цикла. Ребра (a,b), (f,g) выбраковываются, а добавляется следующие ребра (f,h), (c,i). На этом построение минимального каркасного дерева закончено (рис. 42).