5.12. Гамильтоновы графы

Гамильтоновой цепью называется простая цепь, приходящий через каждую вершину графа ровно один раз.

Гамильтоновым циклом (англ. Hamiltonian cycle) называется замкнутая гамильтонова цепь.

Граф называется гамильтоновым (англ. Hamiltonian graph), если он содержит гамильтонов цикл.

Граф называется полугамильтоновым (англ. Semihamiltonian graph), если он содержит гамильтонову цепь.

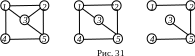
В графе, изображенном на рис. 31 слева, гамильтоновым циклом является, например, последовательность 1, 2, 3, 5, 4, 1. В графе, изображенном в центре, нет гамильтоновых циклов, но есть гамильтоновы цепи, например, 2,5,3,1,4. В правом графе нет и гамильтоновых цепей.

Гамильтоновы графы применяются для моделирования многих практических задач, например, служат моделью при составлении расписания движения поездов. Основой всех таких задач служит классическая задача коммивояжера: коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.

В отличие от поиска эйлеровых циклов, проходящих через каждое ребро графа по одному разу, для которых еще Эйлером получено необходимое и достаточное условие существования цикла, для гамильтоновых циклов такого условия не найдено. Для гамильтоновых циклов и путей неизвестно никаких просто проверяемых необходимых и достаточных условий их существования, а все известные алгоритмы требуют для некоторых графов перебора большого числа вариантов.

Достаточные условия гамильтоновости графа формулируются в виде терем.

Теорема Дирака. Простой граф порядка n≥3 гамильтонов, если степень любой его вершины удовлетворяет неравенству

.

Граф, удовлетворяющий неравенству, называется графом Дирака. Каждый граф Дирака обязательно гамильтонов. Однако, встречаются гамильтоновы графы, не являющиеся графами Дирака. Граф на Рис. 32 будучи гамильтоновым, не является графом Дирака.

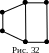
Известно, что каждый полный граф – гамильтонов, потому что в нем проведены все возможные ребра, благодаря чему возможен обход по всем вершинам.

Теорема Оре. Граф (n≥3) гамильтонов, если степени любых двух его несмежных вершин и удовлетворяют неравенству

_.

Граф с выполненным условием теоремы, называется графом Оре. Переформулировав теорему Оре, можно сказать, что если степени любых двух несмежных вершин не меньше общего числа вершин в графе, то граф обязательно является графом Оре. Каждый граф Оре – гамильтонов граф, но обратное утверждение не верно.

На рис. 33 приведен пример графа Оре.

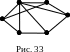
Для ориентированных графов также имеется достаточное условие гамильтоновости.

Теорема Гуйя-Ури. Связный орграф обладает гамильтоновым циклом, если для любой его вершины v_i выполняется условие:

, .

В качестве метода построения гамильтоновой цепи рассмотрим метод последовательного перебора. В ходе выполнения алгоритма строится отрезок пути, который хранится в стеке PATH. На каждом шаге путь наращивается дугой, связывающей последнюю вершину со смежной, не включенной в цепь, до тех пор, пока не будет обнаружена гамильтонова цепь или все возможные пути не будут исследованы.

Пример 5.6. Построить гамильтонов цикл для орграфа, изображенного на рис. 34.

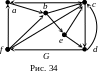
Для графа G можно описать окрестность Г каждой вершины: В качестве исходной выбираем вершину а, поэтому в начале стек PATH={a}. Фиксируем вершину a в первой позиции. Единственной доступной из вершины a является вершина b, поэтому включаем ее в стек PATH=

Наращиваем цепь из вершины b. Множество Г(b)={c,e} позволяет присоединить одну из дуг (b,с), (b,e). Выбираем вершину c. Образуется PATH Поскольку то на третьем шаге можем присоединить только вершину d, так как вершина уже принадлежит PATH. В _{результате PATH={a,b,c,d}. На четвертом шаге добавляем вершину f и имеем PATH={a,b,c,d,f}. Дальнейшее наращивание становится невозможным, так как все вершины в текущем множестве Г уже содержатся в стеке PATH.}

_{Возвращаемся к вершине d и анализируем ее множество} Вершина f уже была включена с отрицательным результатом, поэтому возвращаемся на шаг ранее к вершине c, а потом и к b. Множество содержит еще не прозондированную вершину e. Получаем PATH Множество позволяет выбрать c PATH _{Г(е) позволяет выбрать с PATH={a,b,е,c}. Еще две итерации позволяют построить PATH={a,b,е,c,d,f}. Поскольку в графе есть дуга (f,a), получаем гамильтонов цикл. Выполненные действия алгоритма наглядно представляются таблицей.}

_{Таблица 30}

Итерация	Цепь	Итерация	Цепь
1	a	7	a,b,c
2	a,b	8	a,b
3	a,b,c	9	a,b,e
4	a,b,c,d	10	a,b,e,c
5	a,b,c,d,f	11	a,b,e,c,d
6	a,b,c,d	12	a,b,e,c,d,f