1.2. Операции над множествами

Объединением (суммой) множеств А и В называется множество элементов, принадлежащих хотя бы одному из данных множеств. Множество содержит элементы, принадлежащие либо множеству А, либо множеству В, либо одновременно множествам А и В. Объединение множеств формально можно описать следующим образом:

.

Для наглядного представления операций с множествами используют диаграммы Венна. В диаграмме Венна все точки прямоугольника образуют универсальное множество U, а круги внутри прямоугольника являются подмножествами А и В.

Объединению множеств соответствует заштрихованная область на рис. 1. Операция объединения множеств коммутативна, т.е. .

Пересечением (произведением) множеств А и В называется множество элементов, принадлежащих одновременно множеству А и множеству В. Пересечение множеств формально можно описать следующим образом:

.

На диаграмме Венна (рис.2) пересечению множеств соответствует заштрихованная область.

Операция пересечения множеств коммутативна, т.е. .

Отметим, что выполняются включения

;

Если А и В — непустые множества, пересечение которых пусто, т. е. А В =Ø, то множества называют непересекающимися.

Разностью множеств А и В называется множество элементов, принадлежащих А и не принадлежащих В. Формально разность множеств описывается следующим образом

.

Разность множеств указана штриховкой на рис. 3

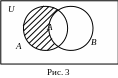
Пример 1.2. Пусть заданы множества , , . Тогда объединение множеств равно: , пересечение , разность множеств = .

Стоит отметить, что в отличие от предыдущих операций разность множеств является некоммутативной операцией, т.е. .

Пример 1.3. Пусть множество А представляет собой промежуток на числовой оси , а множество В-промежуток . Тогда разностью является множество , удовлетворяющее неравенству .

Дополнением множества А до множества U называется множество элементов, которые не содержатся в множестве А, но содержится в множестве U. Дополнение может быть представлено как разность множеств . Множество, соответствующее дополнению , заштриховано на рис. 4.

Пример 1.4. Пусть универсальное множество U-множество всех сотрудников предприятия, А - множество сотрудников старше 40 лет, В – множество менеджеров предприятия, С – множество сотрудников со стажем работы на предприятии более 5 лет. Тогда - множество менеджеров старше 40 лет, - множество сотрудников со стажем работы не более 5 лет, - множество менеджеров, имеющих стаж работы не более 5 лет, - множество сотрудников предприятия со стажем работы более 5 лет, не являющихся менеджерами.

1.3. Основные тождества алгебры множеств

Введенные операции над множествами подчинены некоторым очень простым абстрактным законам. Множество, его подмножества и законы сочетания подмножеств образуют алгебраическую систему, называемую булевой алгеброй. Ниже перечислены основные законы, действующие в булевых алгебрах для универсального множества U, и подмножеств А, В, С.

Законы для объединения и пересечения:

1. = (закон идемпотентности).

2. (закон идемпотентности).

3. (коммутативность операции объединения множеств).

4. (коммутативность операции пересечения множеств).

5. (ассоциативность операции объединения множеств).

6. (ассоциативность операции пересечения множеств).

7. (дистрибутивность операции пересечения относительно операции объединения)

8. (дистрибутивность операции объединения относительно операции пересечения)

9. .

10. Ø=Ø (свойство нуля).

11. .

12. Ø= (свойство нуля).

Законы для дополнений:

1. = (закон двойного отрицания).

2. (закон комплиментарности).

3. =Ø (закон комплиментарности).

4. (закон двойственности).

5. (закон двойственности).

6. =Ø.

Законы для разности множеств:

1. .

2. .

3. =Ø.

4. Ø= .

5. Ø/ =Ø.

6. =Ø.

7. .

8. .

9. .

10. .

Законы поглощения

Доказательство каждого из перечисленных законов основано на определении равенства множеств (взаимовключения множеств). Докажем один из законов двойственности для дополнений: = .

Пусть . По определению операции дополнения это означает, что , но . Следовательно, и одновременно . Таким образом, и х . Из определения операции пересечения получаем, что х . Поэтому, учитывая произвольность элемента х , имеем .

Пусть теперь . Это значит, что одновременно выполняются условия , x или, другими словами, и . Следовательно, .Таким образом, . Поскольку х — произвольный элемент из , то окончательно получаем .