
Учебное пособие 737
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра прикладной математики и механики
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к курсовой работе для студентов направлений
12.03.04«Биотехнические системы и технологии»,
11.03.04«Электроника и наноэлектроника»
(все профили) заочной формы обучения
Воронеж 2021
УДК 517.2.(07) ББК 22.1я7
Составители:
д-р физ.- мат. наук А. В. Келлер, канд. физ.- мат. наук Т. И. Костина, канд. техн. наук А. А. Сидоренко канд. техн. наук О. А. Соколова
Математика: методические указания к курсовой |
работе для |
|||
студентов направлений |
12.03.04 |
«Биотехнические |
системы |
|
и технологии», |
11.03.04 |
«Электроника и наноэлектроника» |
||
(все профили) |
заочной |
формы |
обучения / ФГБОУ ВО |
|
«Воронежский государственный технический университет»; сост.: А. В. Келлер, Т. И. Костина, А. А. Сидоренко, О. А. Соколова. Воронеж: Изд-во ВГТУ, 2021. 37 с.
Содержат задания и рекомендации к курсовой работе по высшей математике, программу курса с указанием литературы, примеры решения задач и двадцать вариантов контрольных заданий.
Предназначены для студентов направлений 12.03.04 «Биотехнические системы и технологии», 11.03.04 «Электроника и наноэлектроника» (все профили) заочной формы обучения.
Методические указания подготовлены в электронном виде и содержаться в файле М_КР_БСТ_ЭМ.pdf.
Ил. 6. Табл. 2. Библиогр.: 4 назв.
УДК 517.2.(07) ББК 22.1я7
Рецензент - А. Б. Кущев, канд. физ.-мат. наук, доцент кафедры прикладной математики и механики ВГТУ
Издается по решению редакционно-издательского совета
Воронежского государственного технического университета
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ «МАТЕМАТИКА»
Курсовая работа по дисциплине «Математика» является одним из основных элементов контроля работы студентов в рамках освоения ряда технических специальностей и направлений подготовки и выполняется в последнем семестре изучения данной дисциплины.
Целью курсовой работы является систематизация, закрепление и расширение теоретических знаний и практических умений студентами для решения задач прикладного характера. Курсовая работа, выполняется студентом под руководством преподавателя дисциплины «Математика».
Качество выполнения студентом курсовой работы будет свидетельствовать об уровне его: специальной теоретической подготовки и практических навыков в области построения математических моделей исследования операций, проведение расчетов с использованием стандартных компьютерных программ, навыков реферирования научной периодики.
Основные задачи при выполнении курсовой работы:
обоснование актуальности и значимости темы работы в теории и практике деятельности инженера, постановка цели и задач работы;
составление реферативного обзора научной статьи;
овладение методами математического моделирования при решении практических задач;
овладение методами математического программирования и сетевого планирования и управления;
обеспечение взаимосвязи теоретических и практических аспектов поставленных задач при обосновании выводов и решений, полученных студентами в работе;
развитие навыков использования пакетов прикладных программ при решении математических задач;
формирование навыков самостоятельной исследовательской работы с научной и учебной литературой, цитирования и ссылок на источники, умения грамотно, стройно и логи-
3
чески обосновано излагать свои идеи, мысли, обобщать расчеты, строить графики, таблицы, диаграммы;
овладение различными формами представления результатов исследования.
Если в процессе изучения теоретического материала или при решении задач у студентов возникают вопросы, справиться с которыми самостоятельно не удается, то за помощью можно обратиться к преподавателю на консультации.
Завершающим этапом изучения отдельных частей курса высшей математики является сдача зачетов и экзаменов в соответствии с учебным планом.
Выбор варианта курсовоой работы студентом производится по двум последним цифрам номера студенческого билета в соответствии со следующей таблицей.
|
|
Выбор варианта |
Таблица 1 |
|
|
|
|
||
№ |
Последние две |
№ |
Последние две |
|
варианта |
цифры номера |
варианта |
цифры номера |
|
|
студенческого би- |
|
студенческого би- |
|
|
лета |
|
лета |
|
1 |
01, |
21, 41, 61, 81 |
11 |
11, 31, 51, 71, 91 |
|
|
|
|
|
2 |
02, 22, 42, 62, 82 |
12 |
12, 32, 52, 72, 92 |
|
3 |
03, 23, 43, 63, 83 |
13 |
13, 33, 53, 73, 93 |
|
4 |
04, 24, 44, 64, 84 |
14 |
14, 34, 54, 74, 94 |
|
5 |
05, 25, 45, 65, 85 |
15 |
15, 35, 55, 75, 95 |
|
6 |
06, 26, 46, 66, 86 |
16 |
16, 36, 56, 76, 96 |
|
7 |
07, 27, 47, 67, 87 |
17 |
17, 37, 57, 77, 97 |
|
8 |
08, 28, 48, 68, 88 |
18 |
18, 38, 58, 78, 98 |
|
9 |
09, 29, 49, 69, 89 |
19 |
19, 39, 59, 79,99 |
|
10 |
10, 30, 50, 70, 90 |
20 |
00, 20, 40, 60, 80 |
|
4
ПРОГРАММА ДИСЦИПЛИНЫ «МАТЕМАТИКА» (ТРЕТИЙ СЕМЕСТР)
Кратные и криволинейные интегралы
1. Понятие двойного интеграла. Геометрический смысл. Свойства двойных интегралов. Вычисление двойного интеграла посредством сведения его к двукратному.
2. Переход к полярным координатам в двойном интеграле. 3. Приложения двойного интеграла.
4. Понятие тройного интеграла, его геометрический смысл и свойства. Вычисление тройного интеграла посредством сведения его к трехкратному.
5. Переход к цилиндрическим и сферическим координатам в тройном интеграле.
6. Приложения тройного интеграла.
7.Понятие криволинейного интеграла, его свойства. Вычисление криволинейного интеграла посредством сведения его к определенному.
8.Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования.
9.Приложения криволинейного интеграла.
10. Понятие поверхностного интеграла, его свойства. Вычисление поверхностного интеграла путем сведения его к двойному интегралу. Приложения поверхностного интеграла.
11. Формула Стокса.
12. Формула Остроградского-Гаусса.
Элементы теории поля
1.Скалярноеполе: производная понаправлению, градиент.
2.Векторное поле: поток, дивергенция; циркуляция; ротор поля.
3.Оператор Гамильтона. Оператор Лапласа.
5
Элементы теории функций комплексного переменного
1. Элементарные функции комплексного переменного.
2. Производная функции комплексного переменного. Условия Коши-Римана. Дифференцируемость элементарных функций.
3. Интегрирование по комплексному аргументу. Теорема Коши. Интегральная формула Коши.
4. Ряды Тейлора и Лорана. Изолированные особые точки функции, их классификация.
5. Вычеты. Основная теорема о вычетах. Применение вычетов к вычислению интегралов.
Операционное исчисление
1.Преобразование Лапласа: оригиналы и изображения; свойства преобразования.
2.Обратное преобразование Лапласа.
3.Интеграл Дюамеля.
4.Решение дифференциальных уравнений операционным методом.
5.Решениеинтегральныхуравненийоперационнымметодом.
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КУРСОВЫХ РАБОТ
Выполняется в электронном виде, сдается в бумажном и в электронном виде с отсканированным титульным листом с подписями.
Титульный лист (по образцу смотреть в приложении) Введение должно содержать: 1) обоснование актуально-
сти темы работы в профессиональной деятельности; 2) цель и задачи работы; 3) обзор методов, используемых в работе.
Основная часть в общем случае может состоять из теоретических (научно-исследовательских) и расчетных (произ- водственно-технологических, проектно-конструкторских и др.) разделов.
6
При выборе варианта «типовая курсовая работа» основная часть содержит три раздела: 1) математическое моделирование производственного раскроя (производственного плана, управленческого или технологического решения о назначении, перевозках и т.д.); 2) реферативный обзор научной статьи по тематике курсовой работы 3) управление комплексом технологических работ методами сетевого планированияи управления.
В зависимости от особенностей курсовой работы отдельные разделы допускается исключать, а также вводить новыеразделы в соответствии с требованиями задания накурсовую работу.
Заключение должно содержать: краткие выводы по выполнению поставленных задач; результаты оценки полноты решений и достижение цели, поставленной в работе; выводы об использовании полученных результатов и направлениях дальнейшего исследования проблематики.
Список литературы содержит сведения об источниках, использованных при составлении расчетно-пояснительной записки курсовой работы. Сведения об источниках приводят в соответствии с требованиями ГОСТ 7.1.
ЗАЩИТА КУРСОВОЙ РАБОТЫ
Все курсовые работы защищаются. Защиту принимает комиссия из ведущих преподавателей кафедры. Состав комиссии по защите курсовой работы определяется руководством кафедры. В состав комиссии по защите курсовой работы по дисциплине «Математика» обязательно входит преподаватель этой дисциплины, остальной состав может быть различным в завиимости от даты защиты.
Защита курсовой работы проводится в соответствии с утвержденным заведующим кафедрой графиком защиты курсовых работ.
На доклад по теме курсового проекта студенту предоставляется не более 7 минут. Затем представляется рецензия руководителя на курсовую работу. Если в рецензии содержатся замечания, то члены комиссии предоставляют студенту
7

возможность ответить на них. После этого члены комиссии могут задать ряд вопросов по докладу. Студент должен быть готовк ответуна любой вопросвпределах темыкурсовой работы.
Входе защиты оцениваются умение представить полученные результаты, грамотная речь и ответы на вопросы, уточняются знания студента, а также определяется степень самостоятельности выполнения работы. Комиссия, обсудив результаты защиты, оценивает ее. Затем, с учетом оценки руководителя за курсовую работу и оценки за защиту курсовой работы, определяется окончательная оценка.
Вслучае получения неудовлетворительной итоговой оценки за курсовую работу студент должен внести исправле-
ния и (или) дополнения, а затем может быть допущен к п о- вторной защите в дополнительные сроки. Сроки повторной защиты утверждаются заведующим кафедрой.
ЗАДАНИЯ КУРСОВОЙ РАБОТЫ
Задача № 1
Изменить порядок интегрирования.
1. |
−∫1 dy ∫0 |
f (x, y) dx + ∫0 dy ∫0 |
f (x, y) dx . |
|||||||||||
|
−2 |
− 2+y |
|
|
−1 |
|
|
− |
−y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
y |
|
|
|
|
|
2−y2 |
|
|
|||
|
|
2 |
|
|
|
|||||||||
2. |
∫dy∫ f (x, y) dx + ∫ dy |
|
∫ f (x, y) dx . |
|||||||||||
|
0 |
0 |
|
1 |
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
|
|
2−y |
|
|||||||
3. ∫1 dy ∫ f (x, y)dx +∫2 dy ∫ f (x, y)dx . |
||||||||||||||
|
0 |
0 |
|
1 |
|
|
|
0 |
|
|
|
|
|
|
8
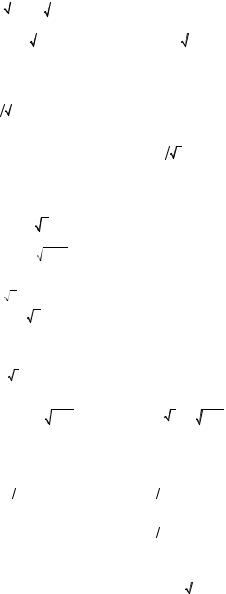
4. |
−∫1 |
dx ∫0 |
f (x, y) dy + ∫0 dx∫0 (f , x) y dy . |
||||||||||||
|
− |
2 |
|
|
− |
2−x2 |
−1 |
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+y |
|
|
|
|
−y |
||||
5. |
−∫1 dy ∫ f (x, y) dx + ∫0 dy ∫ f( ,x )y dx |
||||||||||||||
|
−2 |
0 |
|
|
|
−1 |
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
arcsin y |
1 |
|
|
|
arccos y |
||||||
6. |
∫ dy ∫ |
f (x,y)dx + ∫ dy ∫ f (x,y) dx . |
|||||||||||||
|
0 |
|
|
|
0 |
|
1 |
2 |
0 |
||||||
|
1 |
|
|
|
0 |
|
|
|
|
e |
−ln y |
||||
7. |
∫dy ∫ f (x, y) dx + ∫dy |
|
∫ f (x, y) dx |
||||||||||||
|
0 |
|
|
|
− |
y |
|
1 |
|
−1 |
|||||
8. −∫1 dx
 2∫−x2 f (x, y)
2∫−x2 f (x, y)
−
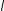 2 0
2 0
13 y
9.∫dy ∫ f (x, y) dx
00
0 x2
dy + ∫dx ∫ f (x, y) dy .
−1 0
22−y
+∫dy ∫ (f , x) y dx
10
10. |
−∫ |
3 |
dx |
|
∫0 |
|
f (x, y)dy + ∫0 |
dx |
∫0 |
f (x, y)dy |
||||||||
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
− |
4−x2 |
− |
3 |
|
|
|
|
4−x2 |
−2 |
|
|
||||
11. |
∫1 |
dx ∫1 |
f (x, y) dy + ∫e dx |
∫1 |
f (x, y) |
dy |
||||||||||||
|
0 |
|
|
1−x2 |
|
1 |
|
|
|
ln x |
|
|
|
|
||||
|
π 4 |
sin y |
|
π 2 |
|
|
|
cos y |
|
|
||||||||
12. ∫ dy ∫ f (x, y) dx + ∫ dy ∫ f (x, y) dx. |
||||||||||||||||||
|
0 |
|
|
0 |
|
π 4 |
|
|
|
0 |
|
|
|
|
||||
13. |
−∫1 dx |
∫0 |
f (x, y) dy + ∫0 |
dx ∫0 |
f (x, y) |
dy . |
||||||||||||
|
−2 |
|
−(2+x) |
−1 |
|
|
|
3 |
x |
|
|
|
|
|
||||
9
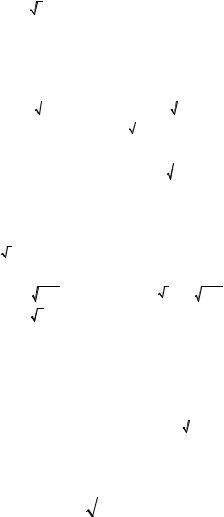
|
|
∫1 |
|
|
y |
|
f (x, y) dx + ∫e dy ∫1 |
|
|
|
|
|
|
|
|
||||||||||||
|
14. |
dy ∫ |
|
f (x, y) dx . |
|||||||||||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
ln y |
|
|
|
|
|
|
|
|
|||||||
|
15. |
∫1 |
dy ∫0 |
|
f (x,y) dx +∫2 dy |
|
|
∫0 |
|
|
|
|
f( |
,x )y dx . |
|||||||||||||
|
|
0 |
− |
y |
|
|
|
|
|
1 |
− |
|
2−y |
|
|
|
|
||||||||||
|
16. ∫1 dy ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
f (x,y) dx + ∫2 |
dy ∫0 |
|
|
|
|
f (x,y) dx . |
||||||||||||||||||||
|
|
0 |
−y |
|
|
|
|
|
|
1 − |
|
2−y2 |
|
|
|
|
|
||||||||||
|
|
1 |
y2 |
|
|
|
|
|
|
2 |
2−y |
|
|
|
|
|
|
|
|
||||||||
|
17. |
∫dy ∫ |
|
f( |
,x )y dx + ∫dy |
∫ |
(f |
,x )y |
dx . |
||||||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
∫0 |
f( ,x )y dy + ∫2 |
|
|
|
∫0 |
|
|
|||||||||||||
|
18. |
∫3 |
dx |
|
dx |
|
f (x,y) dy . |
||||||||||||||||||||
|
|
0 |
|
|
4−x2 |
−2 |
|
|
|
3 |
|
|
|
− |
4−x2 |
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
||
|
19. ∫1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dy ∫ f (x, y) dx + ∫2 dy2∫y |
|
f (x, y) dx |
||||||||||||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
||||||
|
20. |
−∫1 dy ∫0 |
f( ,x )y dx + ∫0 dy ∫0 |
(f ,x )y dx . |
|||||||||||||||||||||||
|
|
−2 |
−(2+y) |
|
|
|
|
|
−1 |
|
|
3 |
y |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача № 2 |
|
|
|
|
||||||||||
Вычислить объем тела, ограниченного поверхностями: |
|||||||||||||||||||||||||||
|
y = x3, |
y = − |
|
, |
x =1, |
|
z = 0, |
z = x + y2. |
|||||||||||||||||||
1. |
x |
|
|||||||||||||||||||||||||
2. |
y = x2, |
|
y = 5x + 6, z = 0, |
|
z = y2. |
||||||||||||||||||||||
3. |
y = x2, |
|
y + x = 6, x = 0, z = 0, z = y. |
||||||||||||||||||||||||
4. |
y = |
8 , |
|
|
|
y + x = 9, |
|
z = 0, |
|
|
|
z = x. |
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10
