
Учебное пособие 733
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
328 - 2012
ВЕКТОРНАЯ АЛГЕБРА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность»
(«Защитавчрезвычайныхситуациях», «Безопасность жизнедеятельностивтехносфере», «Защитаокружающейсреды») очной формы обучения
Воронеж 2012
Составитель канд. физ.-мат. наук И.Н. Пантелеев
УДК 681.3.06
Векторная алгебра: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность» («Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды») очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; Сост. И.Н. Пантелеев. Воронеж, 2012. 49 с.
Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" при изучении в 1 семестре раздела «Векторная алгебра» для студентов специальностей ЧС, БЖ и ЗС. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и
содержатся в файле Vmfmm_VektAg_1.pdf.
Ил. 19. Библиогр.: 8 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2012
ВЕКТОРНАЯ АЛГЕБРА 1. Векторные и скалярные величины.
Линейные операции над векторами
1°. Основные определения. Величина называется скалярной, если она определяется заданием ее числового значения, и векторной, если для ее определения задается еще и ее направление.
Два вектора считаются равными, если они имеют одинаковую длину, параллельны друг другу и одинаково направлены.
Два вектора называются противоположными, если они имеют одинаковую длину, параллельны и противоположно направлены.
Два вектора называются коллинеарными, если они расположены на параллельных прямых (или на одной прямой), независимо от того направлены ли они одинаково или их направления противоположны. Если векторы лежат в одной плоскости или в плоскостях, параллельных между собой, то они называются компланарными.
Вектор, модуль которого равен нулю, называется нуль-
вектором.
Нуль-вектор не имеет направления.
Вектор, модуль которого равен единице, называется
единичным вектором.
Единичный вектор, одинаково направленный с вектором aG, называется ортом вектораa .
2°. Суммой двух векторов a и b называется вектор cG,
построенный следующим образом: перенесем начало вектора
G
b в конец вектора c и построим вектор c так, чтобы его начало совпадало с началом вектора c , а конец — с концом
вектора bG (рис. 1).

Рис. 1 Сумма векторов обладает свойствами сочетательности
и переместительности |
|
G |
|
||
G |
G |
G |
|
|
|
а) ( a |
+ b ) + c = a + ( b + c ), б) a + b = |
b + a . |
|||
Вектор cG |
называется разностью векторов |
G |
, если |
||
a и b |
|||||
сумма векторов |
G |
равна векторуa , т. е. b + c = a . |
|
||
b и c |
|
||||
Если два вектора приведены к общему началу, то их разность есть вектор, соединяющий их концы и направленный от вычитаемого к уменьшаемому (рис. 2).
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
Свойства |
|
|
|
|
|
||||||
|
|
а) |
|
aG +(−b) = aG −b; б) aG −(−b) = aG +b. |
|
|
|||||||
|
|
3°. |
|
Произведением вектора a на скаляр |
λ |
называется |
|||||||
вектор |
|
|
G |
|
G |
коллинеарный вектору |
a , |
модуль которого |
|||||
b |
= λa |
||||||||||||
равен |
|
λ |
|
|
|
aG |
|
. |
|
a |
|
b |
|
|
|
|
|
|
|
|
|||||||
|
|
Если λ >0, направления векторов |
и |
совпадают; |
|||||||||
если λ <0 — направления векторов противоположны.
Свойства
а) λ(μa) = (λμ)a ; б) λa = aλ ; в) λ(aG +b) = λaG +λb .
2
4°. Отношение вектора к его длине илиG модулю называется единичным вектором. Любой вектор a можно
представить с помощью единичного вектора a0 , тогоG же направления, что и вектор a , т. е. a = aG aG0 , откуда aG0 = aaG .
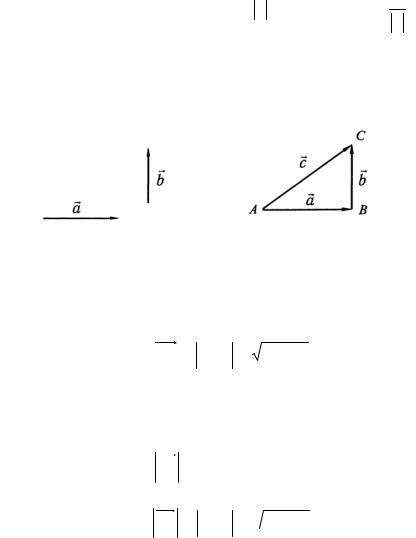
1.1. Даны два вектора a и b |
(рис. 3). Найти их сумму |
и разность. |
|
Решение. а) Векторы a |
и b перпендикулярны. |
Сложение выполняем по правилу треугольника (рис. 4).
Рис. 3 |
|
Рис. 4 |
|
От произвольной точки А отложим вектор a , совместим |
|||
начало вектора |
bG |
с концом вектора |
a , вектор, идущий от |
начала вектора |
aG |
в конец вектора |
b , есть вектор-сумма. |
Модуль вектор-суммы находим по теореме Пифагора
AC = |
G |
G |
= |
a |
2 |
+b |
2 |
. |
a |
+b |
|
|
|||||
б) Совместим начала векторов |
a |
и b и соединим их |
||||||
концы.
Вектор, идущий из конца вектора - «вычитаемого» в конец вектора -«уменьшаемого», есть вектор-разность (рис. 5).
Длина вектора CB может быть найдена по теореме
Пифагора
CB = aG −bG =  a2 +b2 .
a2 +b2 .
РассмотримG еще один способ нахождения разности векторов aG и b .
3
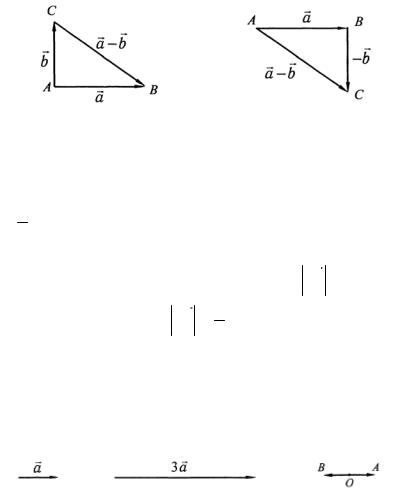
Поместим начало вектора b в конец вектора aG и построим вектор - b , т. е. вектор противоположноG направленный. Поскольку под разностью двух векторов aGGи b
понимают третий вектор, равный сумме векторов a и - b , то вектор-разность находим по правилу треугольника, т. е. это
вектор идущий из начала вектора a в конец вектора - b (рис. 6).
Рис. 5 |
Рис. 6 |
Нетрудно заметить, |
что вектора-разности (рис. 5 и |
рис. 6) равны по величине и направлению, следовательно, они равны.1.2. Дан вектор a (рис. 7). Построить векторы: а) 3 aG;
б) - 32 a .
Решение. а) Увеличиваем модуль вектора a в 3 раза, сохраняя его направление. Получаем вектор OA = 3aG(рис. 8)
б) Строим вектор OA = 23 aG, а затем поворачиваем OА
на 180°.
Получим искомый вектор |
|
JJG |
|
= − |
2 |
aG (рис. 9). Можно |
|
OB |
|
||||
|
|
|
||||
|
|
|
|
3 |
|
|
|
|
|
||||
построить сначала вектор - a , а затем изменить его модуль в
2 |
раза. |
|
|
3 |
|
|
|
|
|
|
|
|
Рис. 7 |
Рис. 8 |
Рис. 9 |
|
|
|
4 |
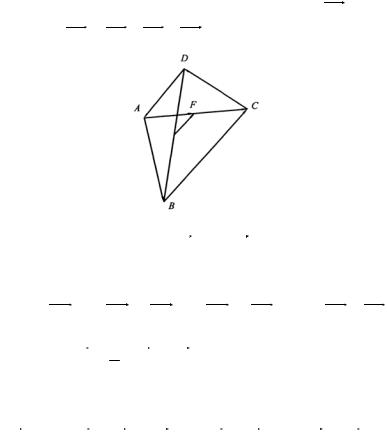
1.3. Доказать, что в произвольном четырехугольнике вектор, соединяющий середины диагоналей, равен геометрической полусумме двух векторов, образующих противоположные стороны четырехугольника.
Решение. Построим четырехугольник и векторизуем стороны и диагонали, как показано на рис. 10. Требуется
|
JJJG |
|
1 |
JJJG |
JJJG |
JJJG |
|
1 |
JJJG JJJG |
|
|
доказать, что |
EF |
= |
|
(BC |
+ DA) или |
EF |
= |
|
(CD + AB) . |
На |
|
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
основании правила сложения векторов вектор EF равен сумме векторов EF = ED + DA + AF .
Рис. 10
Представим векторы EF и AF через векторы сторон четырехугольника
AF = |
1 |
AC ; |
ED = |
1 |
BD; |
ED = − |
1 |
(DA − AB ); |
|
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
AF = 12 ( AB + BC ).
Подставляя найденные векторы в исходное векторное равенство, получим
EF = − |
1 |
(DA + AB) + DA + |
1 |
( AB + BC) = |
1 |
(DA + BC), что и |
|
2 |
2 |
2 |
|||||
|
|
|
|
требовалось доказать. Аналогично доказывается и второе векторное равенство.
5

1.4. Разложить высоту DO правильной
треугольной Gпирамиды (рис. 11) по некомпланарным векторам aG, b , cG.
Рис. 11
Решение. Поскольку пирамида правильная, точка пересечения высоты DO и основания является точкой пересечения медиан основания. Используя свойство точки пересечения медиан треугольника, запишем
DO = DA + AO = −AD + 23 AM .
Поскольку, AM = 12 (AB + AC) , то
DO = −AD + 13 ( AB + AC) = −aG + 13 bG +cG.
1.5. В параллелограмме ABCD точки M,N,P,Q середины сторон (рис. 12).
Рис. 12
6
Выразить |
векторы |
JJG JJJG |
JJJG JJJG |
как линейные |
|||||
AC, AQ, QD, CP |
|||||||||
комбинации векторов AP = a и AN = b . |
|
|
|||||||
Решение. |
JJJG |
G |
JJJJG |
JJJG JJJG |
G |
G |
|||
|
JJG |
JJJG |
|||||||
AC |
= AB |
+ AD |
= 2a |
+2b; AQ = AB + BQ |
= 2a |
+b; |
|||
JJJG |
JJJG |
JJJG |
G |
G JJJG |
JJJG JJJG |
G |
G |
||
QD |
=QC |
+CD =b −2a; CP =CB + BP = −2b |
−a. |
||||||
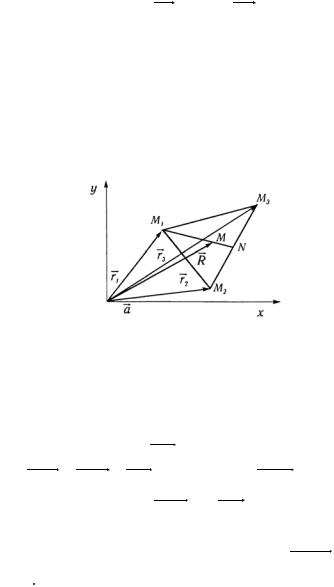
1.6. Однородный треугольник задан радиус-векторами |
|||||||||
r , rG |
, rG своих вершин M1 |
, M2 , M3 . Найти радиус- |
|||||||
1 |
2 |
3 |
|
|
|
|
|
|
|
вектор R центра тяжести.
Решение. Сделаем чертеж (рис. 13).
Рис. 13 Центр тяжести однородного треугольника находится в
точке М пересечения его медиан. Векторизуем стороны треугольника, как показано на рисунке и проведем медиану
M1N. Из свойств медианы следует, что |
JJJJJG |
|
1 |
JJJJJJG |
|||||
M2 N |
= |
|
M2 M3 и |
||||||
2 |
|||||||||
Радиус вектор OM = RGнаходим как сумму векторов |
|||||||||
R = OM |
2 |
+ M |
2 |
N + NM . Вектор OM |
2 |
= rG . |
|
Представим |
|
|
|
|
|
2 |
|
|
|||
выражения векторов M 2 N и NM через известные векторы
r1, r2 , r3 . |
|
|
|
|
|
|
= rG |
− rG |
|
|||
|
|
Из треугольника ОМ2М3 |
находим M |
2 |
M |
3 |
, тогда |
|||||
|
|
|
|
|
|
|
|
3 |
2 |
|
||
M |
2 |
N = |
1 |
(rG |
− rG ) . Из треугольника M1 M2 |
N |
находим |
|||||
|
||||||||||||
|
2 |
3 |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
NM1 |
= −(M1M 2 |
+ M 2 N ) ; |
из |
|
треугольника |
ОМ2М1 находим |
|||||||||||||||||||||||
M |
|
M |
|
= rG −rG . Отсюда: NM |
|
= −(rG |
−rG |
+ |
1 |
|
( r −r ))= |
||||||||||||||||||
1 |
2 |
1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
2 |
1 |
2 |
|
|
3 |
2 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
= rG |
− |
(rG |
+ rG); |
NM = |
(rG |
− |
(rG |
+ rG)). Подставляя найденные |
|||||||||||||||||||||
|
3 |
|
|||||||||||||||||||||||||||
1 |
|
2 |
2 |
|
3 |
|
|
|
|
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|||||||
значения |
векторов |
в |
выражение суммы векторов, получим |
||||||||||||||||||||||||||
R = rG |
+ |
1 |
|
(rG |
− rG ) + |
1 |
(rG |
− |
1 |
(rG |
+ rG )) = |
|
1 |
(rG + rG |
+ rG ). |
||||||||||||||
|
|
|
2 |
3 |
|||||||||||||||||||||||||
|
|
2 |
|
2 |
|
3 |
2 |
3 |
1 |
|
|
2 |
|
3 |
|
|
1 |
|
|
2 |
3 |
|
|||||||
|
|
|
|
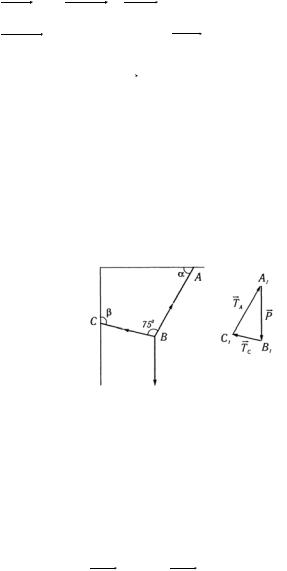
1.7. |
Электрический |
фонарь |
|
весом |
3кг |
подвешен к |
|||||||||||||||||||
потолку на шнуре АВ и затем притянут к стенке веревкой ВС
(рис. 14).
Определить натяжение шнура и веревки, если известно, что угол α=60° , угол β=135°.
Рис. 14 G Решение. На точку В действует две силы TA , TC и P —
вес лампы. Поскольку система сил находится в равновесии, то равнодействующая этих сил равна нулю.
Построим треугольник сил. В выбранном масштабе строим вектор P (рис. 14). Через начало этого вектора проведем линиюGдействия силы TA , а через конец — линию действия силы TC . Получим треугольник А1В1С1. Векторизуем
его стороны B1C1 = TGC , C1 A1 = TGA. Модули этих сил найдем по
теореме синусов.
Для этого определим углы при вершинах треугольника.
8
По условию задачи угол при вершине А1 равен 30°, при вершине B — 45°, значит, угол при вершине C1 равен 105°.
Учитывая, что sinl05°=sin75°, по теореме синусов имеем
|
|
TA |
= |
|
TC |
= |
P |
|
|
|
sin 45D |
sin 30D |
sin 75D |
||||
|
|
|
|
|||||
Откуда T =3 sin 45D ≈ 2,19 |
кг; |
T |
=3 sin 30D ≈1,55 кг. |
|||||
A |
sin 75D |
|
|
|
C |
sin 75D |
||
|
|
|
|
|
||||
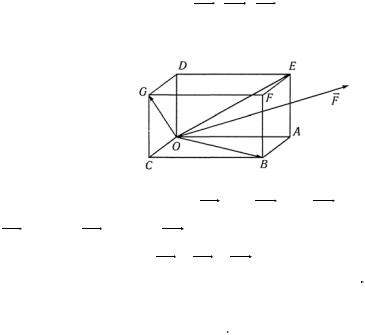
1.8. К вершине О прямоугольного параллелепипеда |
||||||||
ABCOGDEF (рис. 15) приложены три силы, |
||||||||
изображаемые векторами OE, OG, OB , найти величину и |
||||||||
направление равнодействующей |
F . |
|
|
|
||||
Рис.15
Решение. Обозначим OA = aG, OC = bG, OD = cG, тогда
OB = aG +bG, OE = aG +cG, OD = bG +cG.
Поскольку FG = OB +OE +OG , то
FG = aG +bG + aG +cG +bG +cG = 2(aG +bG +cG) = 2OF,
т. е. равнодействующая F изображается удвоенной диагональю параллелепипеда OF .
2. Разложение вектора по координатным осям
1°. Всякий вектор в пространстве можно представить как сумму трех векторов, один из которых расположен на оси Ох, второй на оси Оу и третий — на оси Oz
9
