
Учебное пособие 609
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
327 - 2012
ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность»
(«Защитавчрезвычайныхситуациях», «Безопасность жизнедеятельностивтехносфере», «Защитаокружающейсреды») очной формы обучения
Воронеж 2012
Составитель канд. физ.-мат. наук И.Н. Пантелеев
УДК 681.3.06
Числовые и функциональные ряды: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность» («Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды») очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; Сост. И.Н. Пантелеев. Воронеж, 2012. 48 с.
Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы
по курсу "Высшая математика" при изучении во 2 семестре раздела «Числовые и функциональные ряды» для студентов специальностей ЧС, БЖ и ЗС. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и содержатся в файле Vmfmm_ChRd1.pdf.
Ил.4. Библиогр.: 8 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2012
1. ЧИСЛОВЫЕ РЯДЫ
1.1. Сходимость и расходимость ряда. Необходимый признак сходимости
Пусть задана некоторая бесконечная последовательность чисел
ax , a2 ,..., an ,... .
Тогда выражение
∞ |
|
∑an = a1 +a2 +a3 +... +an +... |
(1) |
n=1
называется числовым рядом, а сами числа ax , a2 ,... - членами
ряда. Сумма n первых |
членов ряда |
называется п-й |
частичной суммой ряда |
и обозначается Sn : |
|
n |
|
|
Sn = ∑ak |
= a1 +a2 +... +an . |
(2) |
k =1 |
|
|
Если существует предел S бесконечной |
последовательности |
|
чисел S1, S2 ,..., Sn ,... , т.е. |
|
|
lim Sn = S , |
(3) |
|
n→ ∞ |
|
|
то этот предел называют суммой ряда (1), а сам ряд (1) в этом
случае называется сходящимся. Если же предел lim Sn не
n→∞
существует, то ряд (1) называют расходящимся. Расходящийся
ряд суммы не имеет. Однако, если lim Sn = ±∞, то иногда
n→∞
говорят, что ряд (1) имеет бесконечную сумму.
Пусть ряд (1) сходится. Тогда его частичная сумма Sn
является приближённым значением для |
суммы S . |
Погрешность этого приближения |
|
rn = S −Sn |
(4) |
называется остатком ряда. Этот остаток является суммой ряда:
∞ |
|
rn = ∑ ak = an+1 +an+2 +... |
(5) |
k =n+1

Если ряд (1) сходится, то |
|
lim r = |
0 . |
n→∞ n |
|
Бесконечная геометрическая прогрессия |
|
a +aq +aq2 +... ( a ≠ 0 ) |
(6) |
есть сходящийся числовой ряд, если q <1 . Сумма ряда (6) равна в этом случае
|
|
|
|
|
S = |
|
|
a |
. |
|
|
|
|
|
|
|
1 |
−q |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
В случае |
|
q |
|
≥1 ряд (6) расходится. |
|
|
|||||
|
|
|
|
||||||||
Если ряд (1) имеет сумму S , то ряд |
|
|
|||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
∑c an = ca1 +ca2 +... +ca +... |
(7) |
|
|||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
сходится и имеет сумму c S . Если же ряд (1) расходится, |
то |
||||||||||
(при c ≠ 0 ) расходится и ряд (7). |
|
|
|
||||||||
Сходящиеся ряды можно |
почленно складывать и вычитать, |
||||||||||
т.е., если даны сходящиеся ряды |
|
|
|
||||||||
|
|
|
|
S = a1 +a2 +.. +an +... |
(8) |
|
|||||
то ряды |
|
|
|
σ = b1 +b2 +... +bn +..., |
(9) |
|
|||||
|
|
|
(a1 +b1 ) +(a2 +b2 ) +... +(an +bn ) +... |
(10) |
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
(a1 −b1 ) +(a2 −b2 ) +...+(an −bn ) +... |
(11) |
|
|||||
тоже сходятся, и суммы их соответственно равны S +σ |
и |
||||||||||
S −σ . |
|
|
|
|
|
|
|
|
|
|
|
Свойство |
|
|
|
сходимости |
или |
|
расходимости |
ряда |
не |
||
нарушается, если отбросить или прибавить к нему любое конечное число членов.
Необходимый признак сходимости ряда:
Если ряд (1) сходится, то его общий член стремится к нулю
при n → ∞, т. е. lim an = 0 .
n→∞
2
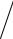
Обратное утверждение неверно. Из того, что lim a |
n |
= 0 , |
n→∞ |
|
∞
сходимость ряда ∑an не следует. Для сходимости ряда общий
n=1
член ряда должен не просто стремиться к нулю, но делать это достаточно быстро.
∞ |
|
=1+ |
1 |
|
1 |
+... + |
1 |
+... , |
Пример 1. Члены ряда ∑1 |
+ |
|||||||
n=1 |
n |
|
2 |
|
3 |
|
n |
|
называемого гармоническим, стремятся к нулю с ростом их
номеров ( lim 1 |
= 0 ), однако этот ряд расходится, его lim Sn = ∞ . |
n→∞ n |
n→∞ |
(Расходимость может быть доказана интегральным признаком).
∞ |
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|
||
Пример 2. Члены ряда ∑ |
= |
+ |
+ |
+... + |
|
+... тоже |
|||||||
n |
2 |
4 |
8 |
|
n |
||||||||
n=1 |
2 |
|
|
|
|
2 |
|
|
|||||
стремятся к нулю с ростом |
их |
номеров |
(lim |
1 |
|
= 0) , но |
|||||||
|
2n |
||||||||||||
|
|
|
|
|
|
|
|
n→∞ |
|
|
|||
убывают быстрее, чем члены гармонического ряда. Этот ряд уже является сходящимся, его сумма может быть найдена по формуле суммы бесконечно убывающей геометрической прогрессии:
S = |
|
|
a |
= |
1 |
|
− |
1 |
|
=1. |
|
|
|
1 |
|
1 |
|
|
|||||
1 |
−q |
2 |
2 |
||||||||
|
|
|
|
|
|
||||||
С помощью необходимого признака сходимости нельзя доказать сходимость ряда, но иногда удаётся доказать расходимость, применяя следствие из необходимого признака, которое легко доказывается от противного.
Следствие из необходимого признака сходимости:
Если lim an ≠ 0 , то ряд расходится.
n→ ∞
Пример 3. Выяснить, сходится или расходится ряд
∞ |
n |
|
|
|
∑ |
. |
|||
n +1 |
||||
n=1 |
|
|||
3

Общий |
член |
этого |
ряда |
an = |
n |
|
. |
|
n +1 |
||||||||
|
|
|
|
|
|
|||
lim a |
n |
= lim |
n |
= lim |
|
|
1 |
|
=1, т. е. lim a |
≠ 0 . На основании |
|
|
|
|
|
|
1 |
||||||
n→ ∞ |
n→ ∞ n +1 |
n→ ∞ |
1 |
+ |
n→∞ |
n |
|||||
|
|
|
|
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
следствия из необходимого признака заключаем, что данный ряд расходится.
Пример 4. |
Проверить, |
выполняется ли необходимый |
|||||||
|
|
|
|
|
|
∞ |
2n |
|
|
признак сходимости для ряда ∑ |
|
. |
|||||||
|
2 |
||||||||
|
|
2n |
|
|
2 n |
n=1 n |
+1 |
|
|
lim a |
= lim |
|
= lim |
= 0 . |
Необходимый признак |
||||
|
|
1+1 n2 |
|||||||
n→∞ n |
n→∞ n2 +1 |
n→∞ |
|
|
|
|
|||
выполняется, поэтому ряд может быть как сходящимся, так и расходящимся, что можно установить лишь после дополнительного исследования.
Исследование сходимости рядов, как правило, сводится к вычислению некоторых пределов, при этом часто используются известные условия эквивалентности бесконечно
малых, которые применительно к рядам принимают вид при n → ∞:
|
|
sin |
1 |
|
1 |
, |
|
tg |
1 |
|
1 |
, |
|
|
|
+ |
1 |
|
|
1 |
, |
|
|
|
|
||
|
|
n |
n |
|
n |
n |
ln 1 |
|
|
n |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
1 |
, arctg 1 1 , |
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||
|
|
arcsin |
|
en |
−1 |
, |
|
|
|
||||||||||||||||||
|
|
|
|
n |
|
n |
|
|
|
|
n |
|
n |
|
|
|
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n! |
2πn |
|
|
|
(формула Стирлинга). |
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Часто также приходится иметь дело с пределами: |
|
|
|
||||||||||||||||||||||||
|
ln n |
(p > 0), |
|
|
|
|
|
1 n |
= e , |
|
|
|
|
n |
n |
p |
|
||||||||||
lim |
n |
p = 0 |
lim |
1 |
+ |
|
|
|
lim |
|
|
|
=1. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
n→ ∞ |
|
|
|
|
|
|
|
|
n→ ∞ |
|
|
|
n |
|
|
|
n→ ∞ |
|
|
|
|
||||||
4
1.2. Ряды с положительными членами. Достаточные признаки сходимости
Рассмотрим числовые ряды с положительными членами:
∞ |
|
|
|
|
|
∑an |
= a1 +a2 +... +an +... |
(an > 0) , |
(1) |
||
n=1 |
|
|
|
|
|
∞ |
|
|
|
|
|
∑bn |
= b1 +b2 +... +bn +... |
(bn > 0) . |
(2) |
||
n=1 |
|
|
|
|
|
Первый признак сравнения. Если для n ≥ n0 an ≤ bn |
и ряд (2) |
||||
сходится, то сходится также и ряд (1). Если для n ≥ n0 |
an ≥ bn и |
||||
ряд (2) расходится, то расходится и ряд (1). |
|
||||
Второй признак сравнения. Если |
существует конечный |
||||
и отличный от нуля предел |
|
|
|||
|
lim |
an |
= A ≠ 0 |
, |
|
|
|
|
|||
|
n→∞ b |
|
|
||
|
|
n |
|
|
|
то ряды (1) и (2) сходятся или расходятся одновременно. |
|||||
При использовании признаков сравнения исследуемый ряд часто сравнивают или с бесконечной геометрической прогрессией
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑a qn (a ≠ 0) , |
||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
которая при |
|
q |
|
<1 сходится, а при |
|
|
q |
|
≥1 расходится, |
|||||
|
|
|
|
|||||||||||
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
или с рядом Дирихле ∑ |
|
(р - |
действительное число). При |
|||||||||||
p |
||||||||||||||
|
|
|
|
n=1 |
n |
|
|
|
|
|
||||
p =1 этот ряд является гармоническим. |
||||||||||||||
Признак Даламбера. Пусть для ряда (1) |
||||||||||||||
|
|
|
|
|
lim |
an+1 |
= q . |
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
n→∞ a |
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
Если q < 1, то ряд сходится, если q > 1, то ряд расходится. При q = 1 вопрос о сходимости ряда остаётся нерешённым.
5
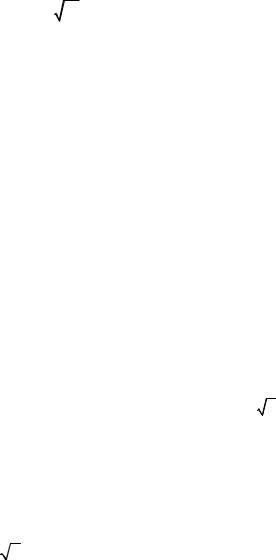
Признак Коши. Пусть для ряда (1)
lim n an = q .
n→∞
Если q < 1, то ряд сходится, если q > 1, то ряд расходится. При q = 1 вопрос о сходимости ряда остаётся нерешённым.
Интегральный признак. Если f (x) - неотрицательная невозрастающая функция при x>0, то ряд
∞
∑ f (n)
n=1
сходится или расходится одновременно с интегралом
∞∫ f (x)dx.
1
Замечание 1. Нижним пределом интегрирования может быть любое другое положительное число из области определения функции.
Замечание 2. С помощью интегрального признака легко доказать, что ряд Дирихле
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
||
|
|
|
|
|
|
p |
|
|
|
|
|
|||
|
|
|
|
|
|
n=1 |
n |
|
|
|
|
|
||
сходится при р > 1 и расходится при р ≤ 1. |
∞ |
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1. Выяснить, сходится или расходится ряд ∑ |
|
. |
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n=1 |
n |
|||
Данный ряд |
знакоположительный. |
Сравним |
его |
|
с |
|||||||||
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
гармоническим рядом |
∑ |
, |
который |
расходится. |
Члены |
|||||||||
n |
||||||||||||||
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|||
данного |
ряда |
|
|
больше соответствующих |
членов |
|||||||||
гармонического ряда: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
≥ |
1 |
(n=1,2,3,…). |
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
|
||||
По первому |
признаку |
|
сравнения |
из расходимости |
||||||||||
6

гармонического ряда следует расходимость данного ряда. Замечание. Расходимость данного ряда можно доказать с
помощью интегрального признака или просто указать, что ряд
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∑ |
|
|
|
есть ряд Дирихле при p = 1/2. Так как р< 1, |
то ряд |
||||||||||||
|
|
n |
|||||||||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
расходится. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример 2. Выяснить, сходится или расходится ряд |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
∞ |
|
2 |
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
n=1 |
3 |
|
|
|
|||
Данный |
ряд |
знакоположительный. Сравним его |
с |
рядом |
|||||||||||||
∞ |
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
∑ |
|
|
|
, который |
является |
|
сходящейся геометрической |
||||||||||
|
|
|
|||||||||||||||
n=1 |
|
3 |
|
|
2 <1. |
|
|
|
|
|
|
|
|
||||
прогрессией с |
q = |
По |
первому признаку |
сравнения |
|||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
сравним соответствующие члены двух рядов: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2n |
< |
2n |
|
(n=1,2,...). |
|
|
||
|
|
|
|
|
|
|
|
|
n |
3 |
n |
|
|
|
|||
|
|
|
|
|
|
|
|
|
n 3 |
|
|
|
|
|
|
|
|
Так как члены данного ряда меньше соответствующих членов
сходящегося ряда ∑∞ 2 n , то данный ряд сходится. n=1 3
Пример 3. Выяснить, сходится или расходится ряд
∑∞ sin 1.
n=1 n
Данный ряд является знакоположительным. Применим второй признак сравнения, и выберем гармонический ряд
∑∞ 1 , который является расходящимся. Найдём
n=1 n
7
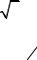
|
an |
|
sin |
1 |
|
|
|
=α |
|
= lim sin |
α |
|
||||
|
|
|
|
1 |
|
|
||||||||||
lim |
= lim |
n |
= |
|
=1. |
|||||||||||
|
|
|
|
n |
|
|||||||||||
|
|
|
|
|
|
|||||||||||
n→ ∞ bn n→ ∞ |
|
1 |
|
|
|
|
α →0 |
|
α→ ∞ |
α |
|
|
||||
|
n |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По второму признаку сравнения данный ряд и гармонический ведут себя одинаково, т. е. из расходимости гармонического следует, что и данный ряд расходится.
Пример 4. Исследовать, сходится или расходится ряд
∞ |
|
1 |
|
|
|
|
∑ |
|
. |
|
|
||
n |
|
|
|
|||
n=1 |
n |
|
|
|||
|
|
∞ |
1 |
|
|
|
Данный ряд перепишем в виде ∑ |
|
. Это - ряд Дирихле при |
||||
3 |
|
|||||
|
|
n=1 |
n |
2 |
|
|
p = 32 . Так как p > 1, то данный ряд сходится.
Пример 5. С помощью интегрального признака доказать сходимость ряда
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
∑ |
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
n=1 n |
+1 |
|
|
|
|
|
|
|||||
Общий член ряда a |
= |
|
|
|
= f (n). |
Записывая в этой формуле |
|||||||||||||||
n2 +1 |
|||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
x вместо п, |
получаем функцию |
f (x) = |
|
. |
Эта функция |
||||||||||||||||
x2 +1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
удовлетворяет условиям |
|
|
|
интегрального |
признака: |
она |
|||||||||||||||
принимает |
положительные |
значения |
|
и |
убывает |
с |
|||||||||||||||
возрастанием x. Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
+∞ dx |
= arctg x |
|
+∞ |
= lim arctg x −arctg1 |
= |
π |
−π = π . |
|
|||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
∫1 x2 +1 |
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
x→∞ |
|
|
|
|
|
2 4 4 |
|
|||||||||
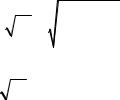
Так как интеграл сходится, то сходится и данный ряд. Замечание. Сходимость данного ряда можно доказать
также по второму признаку сравнения, взяв для сравнения ряд
8
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дирихле ∑ |
|
, |
сходящийся, так как p = 2>1 . |
||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||
n=1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 6. С помощью признака Даламбера выяснить, |
|||||||||||||||||||||||||||||||||||
сходится или расходится ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
2 |
|
n! |
|
|
|
|
|
|
|
|
|
|
||||||||
Общий член |
ряда |
a |
= |
|
|
|
|
|
nn |
|
|
|
. |
|
Заменяя |
|
всюду n на (n+1), |
||||||||||||||||||
|
|
2n |
n! |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
получим: a |
|
|
= |
(n +1)n |
|
|
|
|
|
. |
|
Находим: |
|
|
|
|
|
|
|
||||||||||||||||
n+1 |
2n+1 |
(n |
+1)! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
a |
n+1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
e |
|
||||||
|
|
|
|
|
lim |
|
|
= |
|
|
|
lim |
1 |
+ |
|
|
|
= |
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
2 |
||||||||||||||||||||||||
|
|
|
|
|
n→ ∞ |
a |
|
|
|
|
|
|
2 n→ ∞ |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как e ≈ 2,718 |
, |
значит |
|
>1, |
откуда, |
|
согласно признаку |
||||||||||||||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||||||||||||
Даламбера, ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пример 7. Применяя признак Коши, исследовать, |
|||||||||||||||||||||||||||||||||||
сходится или расходится ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
3n +1 |
n |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
∑ |
2n −1 |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
an |
3n +1 n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Общий член ряда |
= |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
n an |
|
|
|
|
|
|
3n +1 n |
= |
3n +1 |
; |
|
|||||||||||||||||||
|
|
|
|
|
= n |
2n −1 |
|
2n −1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
lim n |
an |
= lim |
3n +1 |
= lim |
|
3 + n |
|
= 3 . |
||||||||||||||||||||||||
|
|
|
2n −1 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
т→∞ |
|
|
n |
→∞ |
|
n→∞ |
|
|
1 |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − n |
|
|
|||
9
